- •Курсовая работа
- •Задание на курсовую работу
- •Красноярск 2013
- •Технические характеристики привода
- •1. Выбор электродвигателя и кинематический расчет.
- •2.3.Проектный расчет закрытой конической прямозубой передачи.
- •4.3. Проверочный расчет ведомого вала на статистическую прочность
- •5.2.Расчет подшипников ведомого вала редуктора (тихоходный вал)
- •6. Выбор муфты
- •7.Выбор системы смазки и сорта масла редуктора, уплотнений.
- •8.Расчет шпоночных соединений.
- •9.Проверка запаса прочности и выносливости валов
2.3.Проектный расчет закрытой конической прямозубой передачи.
Определяем диаметр внешней делительной окружности шестерни.

Коэффициент
К в зависимости от поверхности твердости
 и
и
 зубьев шестерни и колеса соответственно
имеет следущее значения:
зубьев шестерни и колеса соответственно
имеет следущее значения:
-при
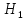 ≤350HB,
≤350HB,
 ≤
350HB K=30;
≤
350HB K=30;
-при
 ≥45
HRC,
≥45
HRC,
 ≤350 HB K=25;
≤350 HB K=25;
-при
 ≥45
HRC,
≥45
HRC,
 ≥45
HRC K=22.
≥45
HRC K=22.
Окружную
скорость
 ,
м/с, на среднем делительном диаметре
вычисляем по формуле:
,
м/с, на среднем делительном диаметре
вычисляем по формуле:

Значение
коэффициентов
 и
и
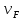 [1,c
45].
[1,c
45].
Уточняем
предварительно найденное значение
диаметра внешней делительной окружности
шестерни, мм:



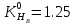

Значение
коэффициента
 внутренней динамической нагрузки для
прямозубых конических колес [1, c
46].
внутренней динамической нагрузки для
прямозубых конических колес [1, c
46].
Значение
коэффициента
 вычисляем ориентировочно:
вычисляем ориентировочно:

Угол делительного конуса шестерни

Внешнее
конусное расстояние

Ширина
зубчатого венца b=(0.2…0.3)*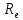 =0.285*156.25=44.53
=0.285*156.25=44.53
Определяем модуль передачи. Внешний торцовый модуль передачи:


Значение
коэффициента
 внутренней динамической нагрузки для
прямозубых конических колес [1,c
35].Для конических колес с круговыми
зубьями значение
внутренней динамической нагрузки для
прямозубых конических колес [1,c
35].Для конических колес с круговыми
зубьями значение
 [1, c 35].
[1, c 35].
Находим
число зубьев шестерни
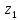 и колеса
и колеса
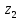 :
:


Полученные значения округляем в блажащую сторону до целого числа.
Фактическое передаточное число определяем как

Отклонение
от заданного значения:


Вычисляем действительные геометрические параметры передачи и сводим их в таблицу.
Таблица 3. Основные геометрические соотношения конических зубчатых передач.
|
Параметры |
Расчетные формулы для прямозубой передачи |
|
Внешний делительный диаметр, мм Шестерни Колесо |
|
|
Внешнее конусное расстояние, мм |
|
|
Угол делительного конуса, град с точностью до 1 Шестерни Колесо |
|
|
Ширина зубьев |
b |
|
Средний модуль, мм. |
|
|
Средний делительный диаметр ,мм Шестерни Колесо |
|
|
Высота головки зуба, мм |
|
|
Высота ножки зуба, мм |
|
|
Угол ножки зуба, град |
|
|
Угол головки зуба, град |
|
|
Внешний диаметр вершин зубьев, мм Шестерня Колесо |
d
|
|
Внешний диаметр впадин зубьев, мм Шестерни Колесо |
|
Находим силы, действующие в зацеплении.



Проверяем передачу на контактную прочность:



 [1,c 34;35].
[1,c 34;35].
Определяем процент перегрузки:

Полученные результаты находятся в пределах допускаемой нормы.
9.Расчетные напряжения изгиба составляет :

Где
 [1,c 36] в зависимости от
эквивалентного числа зубьев колес
[1,c 36] в зависимости от
эквивалентного числа зубьев колес
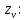 для шестерни
для шестерни 
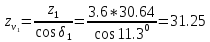

Для колеса:

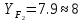
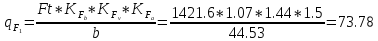 H/mm
H/mm


Расчет выполнялся нами для наиболее слабого звена передачи, найденного сравнением отношений:
для шестерни:
 =94.08
=94.08
для колеса:


3.Расчет открытых передач.
Расчет плоскоременной передачи.
Тип плоского ремня выбираем в зависимости от условий работы и практических рекомендации.
- кордошнуровые
прорезиненные ремни рекомендуются для
передачи широкого диапазона мощностей
при спокойных нагрузках до скоростей
ν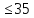 м/с.
м/с.
Определяем диаметр ведущего( малого) шкива передачи, исходя из условия долговечности[1, c78;79]:
-для
кордошнуровых ремней

Определяем скорость ремня, м/с, и сопоставляем ее с оптимальной для принятого типа ремня:
из стандартов

Определяем
диаметр ведомого (большого) шкива
 :
:
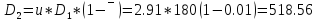 округляем по стандартному ряду
округляем по стандартному ряду
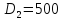
Уточняем передаточное отношение:

Ориентировочно
вычисляем межосевое расстояние [1, c
80] а=2,6* =2,6*180=468
=2,6*180=468
Определяем расчетную длину ремня, мм:

Согласно
табл.3.3[1, c 79]
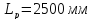
На долговечность передачу проверяем по числу пробегов ремня ν.


Находим
уточненное межосевое расстояние, мм, и
производим расчет только для передач
с бесконечным ремнем при окончательно
установленной длине ремня по стандарту:
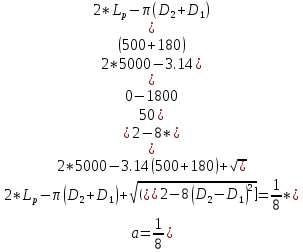
10.Определяем
угол обхвата ремнем малого шкива
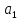 ,
град, и при необходимости увеличиваем
межосевое расстояние a
или применяем натяжной ролик:
,
град, и при необходимости увеличиваем
межосевое расстояние a
или применяем натяжной ролик:

Допускаем
[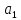 ]≥
]≥
Определяем допускаемую приведенную удельную окружную силу рассчитываемой передачи, Н/мм:

 [1,c 78];
[1,c 78]; [1,c 82];
[1,c 82]; [1,c
82];
[1,c
82]; [1,c
82];
[1,c
82];
 [1,
c 83].
[1,
c 83].
Вычисляем окружную силу, Н, по формуле

По расчету тяговой способности определяем требуемую ширину ( поперечного сечения) ремня b:
- для синтетических и кордошнуровых ремней
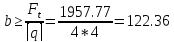
Округляем b=100
Сила давления на валы и опоры зависит от способа регулировки натяжения ремня:
- при
автоматическом регулировании Q=2*
Устанавливаем ширину шкива
В=112[1, c 84]
4.Расчет валов
редуктора
4.1.Расчет валов.
Быстроходный [2, c 112]
Муфта





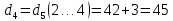 [2, c 435] подшипник 46309
[2, c 435] подшипник 46309
D=100
B=25



 -
граф.
-
граф.
 -граф.
-граф.

Все округления [2, c 326]
Тихоходный [2, c 112]
Колесо (Шкив)
 Т=176,2
Т=176,2




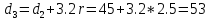
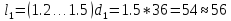
 =1.25*45=56.25
=1.25*45=56.25 56
56

Все округления [2, c 326]
4.2. Проверочный
расчет ведущего вала на статистическую
прочность
Ведущий вал (быстроходный вал)

рис. 1
Дано:
Ft1 = 1421, 6 H;
Fr1 = 501, 54 H;
Fa1 = 102, 36 H;
Fм.
=
 Н
Н
LБ = 134 мм; L1 = 45 мм d1 = 53, 32 мм
LМ = 75 мм;
На рис. 1 составляем расчетную схему вала, проставляем все действующие на вал силы и определяем реакции опор:
Вертикальная плоскость:
а) определяем опорные реакции
∑
М3
= 0 – Fr1
· (L1 + LБ)
+ RАУ
·LБ
+ Fа1
 = 0
= 0
RАУ
=

∑
М2
= 0 – Fr1
· L1
+ RВУ
·LБ
+ Fа1
 = 0
= 0
RВУ
=

Проверка: –RАУ + RВУ + Fr1 = – 650 + 148 –501,54= 0
б) строим эпюру изгибающих моментов относительно оси Х в характерных сечениях 1…3, Нм
Мх1 = Fа1
 = 102,36·
= 102,36· =
2729 Н·мм = 2,7 Н·м ;
=
2729 Н·мм = 2,7 Н·м ;
Мх2
= Fа1
 – Fr1·
L1
= 102,36 ·
– Fr1·
L1
= 102,36 ·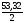 –
501,54·45
= – 19840
Н·мм =
–
501,54·45
= – 19840
Н·мм =
= – 19,8 Н·м;
Мх3 = 0
Горизонтальная плоскость:
а) определяем опорные реакции
∑ М3 = 0 – Ft1 · (L1 + LБ) + RАX ·LБ – Fм ·LМ = 0
RАХ
=

∑ М2 = 0 –Ft1 · L1 + RВX ·LБ – Fм ·(LМ + LБ) = 0
RВХ
=

Проверка: RBX – RAХ + Ft1 – Fм = 958 – 2071,4 + 1421,6 – 308 = 0
б) строим эпюру изгибающих моментов относительно оси Х в характерных сечениях 1…4, Нм
Му1 = 0 Му2 = Ft1 · L1 = 1421,6·45 = 63972Н·мм = 64 Н·м;
Му4 = 0 Му3 = – Fм ·LМ = – 308 ·75 = –23100 Н·мм = – 23,1 Н·м;
Строим эпюру крутящих моментов, Н·м
Мк
= Мz
= Ft1
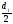 =
1421,6
=
1421,6
 = 37899 Н·мм = 38 Н·м
= 37899 Н·мм = 38 Н·м
Суммарные реакции:
RA
=
 =
=

RB
=
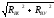 =
=

Определяем суммарные изгибающие моменты в наиболее нагруженных сечениях, Н·м
М2 =
 =
=
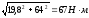
М3 = МУ3 = 23,1 Н·м



 0.5*2*
0.5*2*

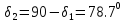
 0.285*
0.285*
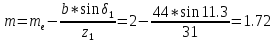








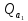 =
=