
- •Примеры проектирование структур матричных процессоров на основе проекций процессорных элементов.
- •Построение параллельных матричных систем на примере умножения двух матриц.
- •Анализ и синтез сп-моделей сложных систем. Декомпозиция моделей.
- •Синтез сп-моделей сложных систем. Типы геометрий.
- •Построение тензорных уравнений.
- •Синтез сп-моделей. Программы синтеза.
- •Синтез сп-моделей. Редукция сетей Петри.
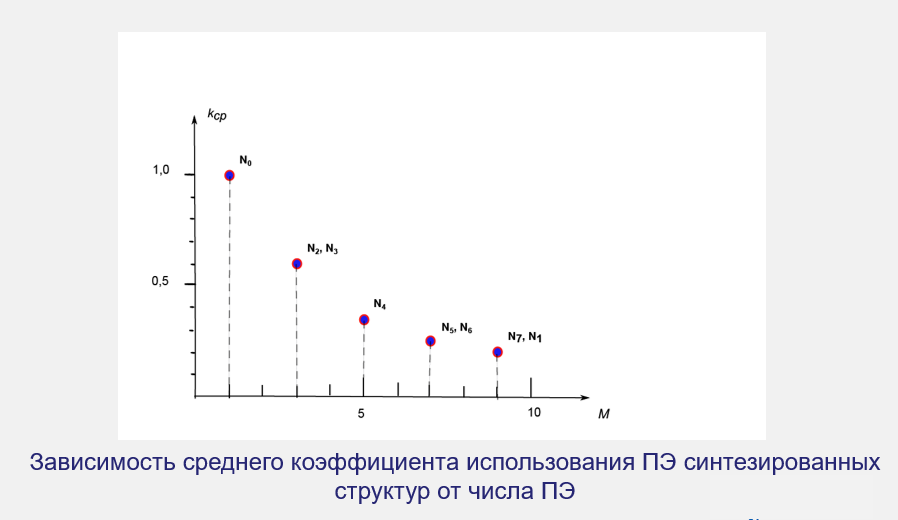
- •Сравнительная оценка синтезированных сетей Петри.
Синтез сп-моделей. Редукция сетей Петри.

Изоморфный – в данном контексте одинаковый

П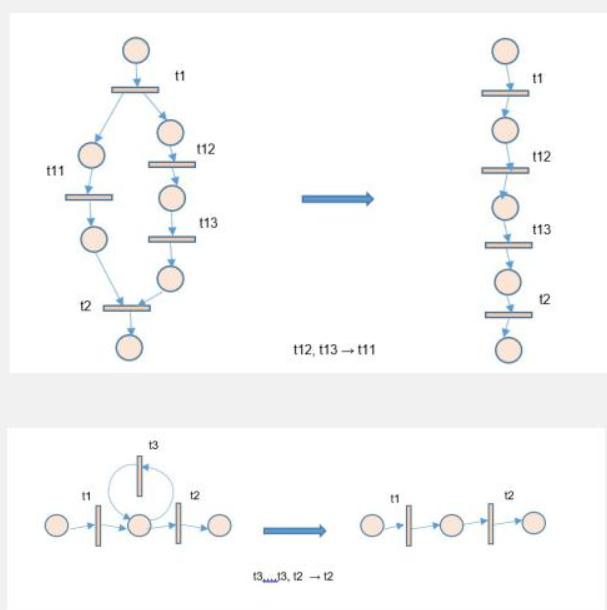 реобразование
G1
реобразование
G1
Если в СП имеется несколько эквивалентных переходов, то может быть оставлен только один из них.
Преобразование G2 (удаление перехода-петли).
Если в СП имеется два перехода t1 и t2 такие, что: pre(t2) = post(t2), pre(t2) pre(t1) (или post(t2) post(t1)), то переход t2 может быть удален.
П реобразование G3 (удаление
позиции-петли).
реобразование G3 (удаление
позиции-петли).
Если в СП имеется позиция p , для которой pre(p) = post(p), то она может быть удалена.
Преобразование G4 (удаление эквивалентных позиций).
Если в СП имеется несколько эквивалентных позиций, то может быть оставлена только одна из них.
Сравнительная оценка синтезированных сетей Петри.





ML. Основные понятия.
Машина просматривает входные данные и соответствующие ответы и выясняет, какими должны быть правила. В машинном обучении система обучается, а не программируется явно. Ей передаются многочисленные примеры, имеющие отношение к данной задаче, а она находит там статистическую структуру, которая позволяет выработать соответствующие правила для решения этой задачи.
ML выявляет правила решения задач обработки данных по примерам ожидаемых результатов. То есть при этом нужны три составляющие:
- контрольные входные данные — например, если решается задача распознавания речи, такими данными могут быть файлы с записью речи разных людей. Если нужно классифицировать изображения, понадобятся соответствующие изображения;
- примеры ожидаемых результатов — в задаче распознавания речи это обычно транскрипции звуковых файлов, составленные людьми.
- способ оценки качества работы алгоритма — необходим для определения того, как сильно отклоняются результаты, возвращаемые алгоритмом, от ожидаемых. Оценка используется в качестве сигнала обратной связи для корректировки работы алгоритма. Этот этап корректировки - обучение.
Обучение - процесс автоматического поиска преобразований, создающих полезные представления определенных данных, который управляется сигналом обратной связи — представлениями, подчиненными более простым правилам решения поставленной задачи.
Алгоритмы ML выполняют поиск в предопределенном наборе операций - пространстве гипотез.
Технически ML — это поиск значимого представления и правил по некоторым входным данным в предопределенном пространстве возможностей с использованием сигнала обратной связи.
Глубокое обучение. Принцип действия глубокого обучения. Геометрическая интерпретация глубокого обучения.
Глубокое обучение —подход, делающий упор на изучении последовательных слоев (или уровней) представлений. Число слоев, на которые делится модель данных, называют глубиной модели. Их может быть десятки и сотни.
То, что именно слой делает со своими входными данными, определяется его весами.
Обучение — это поиск набора значений весов всех слоев в сети, при котором сеть будет правильно отображать образцы входных данных в соответствующие им результаты.
Функция потерь сети, целевая функция, функция стоимости. Принимает ФР и ОР и вычисляет оценку расстояния между ними (определяет успешность)
Оптимизатор реализует алгоритм обратного распространения ошибки — центральный алгоритм (определяет изменение весов в зависимости от функции потерь).
Сначала у весов случайные значения. При повторении весы корректируются.
Обученная сеть – сеть выдающая результаты, близкие к истинным
Это цикл обучения, который повторяется достаточное количество раз (обычно десятки итераций с тысячами примеров) и порождает весовые значения, минимизирующие функцию потерь. Сеть с минимальными потерями, возвращающая результаты, близкие к истинным, называется обученной сетью.
Геометрическая интерпретация – представим 3д объект, который нужно обработать, каждый уровень – это каждый dimension.
История ML. Вероятностное моделирование. Метод опорных векторов. Деревья решений.
Вероятностное моделирование — применение принципов статистики. Это одна из самых ранних форм ML, которая до сих пор используется.
Наи́вный ба́йесовский классифика́тор — простой вероятностный классификатор, основанный на теореме Байеса с наивными предположениями о независимости входных данных. Условия довольно упрощены. Часто работают намного лучше нейронных сетей во многих сложных жизненных ситуациях. Нужно малое количество данных, необходимых для обучения, оценки параметров и классификации.
С байесовским алгоритмом тесно связана модель логистической регрессии (это алгоритм классификации). Была разработана задолго до появления компьютеров, но до сих пор востребована.
Ядерные методы — применение принципов статистики к анализу. Группа алгоритмов классификации. Самый известный – метод опорных векторов. Предназначен для поиска хороших «решающих границ», разделяющих два класса. Он выполняется в два этапа
Д
 анные
отображаются в новое пространство
более высокой размерности, где граница
может быть представлена как гиперплоскость
анные
отображаются в новое пространство
более высокой размерности, где граница
может быть представлена как гиперплоскостьразделяющая гиперплоскость вычисляется путем максимизации расстояния от гиперплоскости до ближайших точек каждого класса - максимизацией зазора.
Деревья решений — это иерархические структуры, которые позволяют классифицировать входные данные или предсказывать выходные значения по заданным исходным значениям.
----
В 2011 почти все инвестиции (менее миллиарда $) уходили в поверхностное ML
К 2015 году вложения превысили пять миллиардов, а в 2017 достигли 16 миллиардов.
Инструменты упростились, что увеличило порог входа. Сейчас для исследований в области глубокого обучения достаточно базовых навыков программирования на Python, Theano, TensorFlow, других библиотек по обработке данных
Математические основы нейронных сетей.
класс – категория в задачи классификации.
образец - Элементы исходных данных.
Метка - Класс, связанный с конкретным образцом.
Слой - фильтр для данных: он принимает их и выводит в более полезной форме. Извлекают представления из входных данных.
Чтобы подготовить модель к обучению, нужно настроить еще три параметра для этапа компиляции:
·оптимизатор, функцию потерь (см вопрос 39)
·метрики для мониторинга — важна точность (доля правильно классифицированных изображений).
Линейная - основа. многие операций задействуют матрицы и векторы.
Матрицы - для представления весов и смещений нейронов, векторы - для представления входных данных и выходов нейронов. Операции сложения, умножения, и транспонирования матриц позволяют эффективно вычислять результаты нейронных сетей.
Линейные уравнения и СЛАУ - для оптимизации параметров нейронных сетей. Методы оптимизации, такие как градиентный спуск, позволяют обновлять веса нейронной сети.
Нейронные сети. Представление данных.
См вопрос про глубокое обучение
тензоры - основная структура данных. Тензор - контейнер для чисел. Матрицы - это двумерные тензоры. Тензоры — это обобщение матриц с произвольным количеством измерений (в терминологии тензоров измерения часто называют осями). Тензор, содержащий единственное число, называется скаляром или тензором нулевого ряда.
Одномерный массив - вектором, или тензором первого ранга.
Например: вектор x = (12, 3, 6, 14, 7) – тензор первого ранга (одна ось) – пятимерный вектор
Мерность может обозначать или количество элементов на данной оси или количество осей в тензоре, что путает.
Массив векторов — это матрица, или тензор второго ранга, или двумерный тензор. Матрица имеет две оси (часто их называют строками и столбцами).
Тензор определяется тремя ключевыми атрибутами, такими как:
- количество осей (ранг)
- форма — кортеж целых чисел, описывающих количество измерений на каждой оси тензора. Вектор имеет форму с единственным элементом, например (5), тогда как у скаляра форма пустая — ();
- тип данных;
Нейронные сети. Представление данных. Примеры.
См вопрос про глубокое обучение
векторные данные — двумерные тензоры с формой (образцы, признаки), где каждый образец — это вектор числовых атрибутов («признаков»);
временные ряды или последовательности — трехмерные тензоры с формой (образцы, метки_времени, признаки), где каждый образец является последовательностью (длиной метки_времени) векторов признаков;
изображения — четырехмерные тензоры с формой (образцы, высота, ширина, цвет), где каждый образец является двумерной матрицей пикселей, а каждый пиксель представлен вектором со значениями «цвета»;
видео — пятимерные тензоры с формой (образцы, кадры, высота, ширина, цвет), где каждый образец является последовательностью (длина равна значению кадры) изображений.
Нейронные сети. Операции с тензорами. Примеры.
Поскольку тензоры можно интерпретировать как координаты точек в некотором пространстве, все операции с тензорами имеют геометрическую интерпретацию. Например сложение тензоров (геометр. сложение векторов) -параллельный перенос объекта на расстояние в направлении.
Параллельный перенос: выше
Поворот: поворот двумерного вектора на угол α выражается как скалярное произведение с матрицей R = [u, v] размером 2 × 2.
Масштабирование: масштабирование изображения по вертикали и горизонтали можно осуществить с помощью скалярного произведения с матрицей 2 × 2:
S = [[масштаб_по_горизонтали, 0], [0, масштаб_по_вертикали]]
Линейное преобразование: скалярное произведение с матрицей. Масштабирование и поворот являются линейными преобразованиями;
Аффинное преобразование: аффинное преобразование —комбинация линейного преобразования и параллельного переноса (путем сложения векторов):
y = W • x + b
Благодаря им можно создать цепочку слоев для реализации очень сложных нелинейных геометрических преобразований и получить богатое пространство гипотез для глубоких нейронных сетей. Свойство аффинных преобразований – при многократном применении аффинного преобразования получается – аффинное преобразование.
Математические основы нейронных сетей. Цикл обучения.
Каждый слой преобразует данные так:
output = relu(dot(input, W) + b) , где relu = max(x,0);
dot – скалярное произведение. W и b — тензоры, являющиеся атрибутами слоя.
Тензоры W и b называются весами или обучаемыми параметрами слоя.
Первоначально весовые матрицы заполняются небольшими случайными значениями - случайная инициализация.
Цикл обучения:
1. Извлекается пакет обучающих экземпляров x и соответствующих целей.
2. Модель обрабатывает пакет x (прямой проход) и получает пакет предсказаний.
3.Вычисляются потери модели на пакете, дающие оценку несовпадения
Между целями и предсказаниями
4.Веса модели корректируются, чтобы уменьшить потери на этом пакете.
На 4 этапе можно применить различные оптимизационные операции. Например, градиентный спуск (см следующий вопрос)
Математические основы нейронных сетей. Оптимизация на основе градиента.
См предыдущий вопрос (цикл обучения)
На этапе подбора весов можно брутфорсить изменения значений каждого веса, что может быть неэффективно, так как весов много.
Градиентный спуск — метод оптимизации, широко применяемый в современных нейронных сетях.
Например, небольшое изменение y в операции z = x + y приведет к небольшому изменению z — и, зная направление изменения y, можно определить направление изменения z.
данные функции дифференцируемы. Если объединить их в цепочку, получившаяся общая функция все равно будет дифференцируемой. Это утверждение, верно для функции, сопоставляющей веса с потерями.
Градиент используется для изменения сразу всех весов в направлении, уменьшающем потери.
Понятие производной применимо к любой функции, если поверхности, которые они описывают, являются непрерывными и гладкими (без острых углов).
Градиенты — обобщение производной на функции, принимающие тензоры
Если производная скалярной функции выражает локальный наклон кривой функции, то градиент тензорной функции выражает кривизну многомерной поверхности, описываемой функцией
Математические основы нейронных сетей. Стохастический градиентный спуск.
См предыдущий вопрос
Там, где градиент равен 0, будет точка минимума функции потерь, и при ней мы получим желаемые значения весов (как с производной) - grad(f(W), W) = 0
Это полиномиальное уравнение с N переменными, где N — число весов в модели. Аналитически решить его при большом N тяжело.
Когда найти точку минимума сложно, используется алгоритм:
1. Извлекается пакет обучающих экземпляров x и соответствующих целей
2.Модель обрабатывает пакет x и получает пакет предсказаний.
3.Вычисляются потери модели на пакете, дающие оценку несовпадения
Между целями и предсказаниями
4.Вычисляется градиент потерь для весов модели (обратный проход). Веса модели корректируются на небольшую величину в направлении, противоположном
градиенту (например, W – (скорость_обучения * градиент)), и тем самым уменьшается функция потерь. Скорость обучения — скалярный множитель, модулирующий «скорость» процесса градиентного спуска.
Термин стохастический означает, что пакет данных выбирается случайно
Проблема – с маленькой скоростью обучения (небольшим изменением весов) найдя локальный минимум, можно в нем застрять, не найдя глобальный минимум:

Идея импульса – для решения проблемы с глобальным минимумом приращение параметра w определяется не только по текущему значению градиента, но и по величине предыдущего приращения параметра.
Математические основы нейронных сетей. Алгоритм обратного распространения ошибки.
См предыдущие вопросы про мат. основы
Имеем функцию fg(x):
X1 = g(x); y = f(x1); return y;
То по правилу цепочек: grad(y, x) = grad(y, x1) * grad(x1, x)
Зная производные f и g, мы можем вычислить производную fg
Нейронная сеть состоит из множества последовательных операций с тензорами, объединенных в одну цепочку, каждая из которых имеет простую известную производную.
Применение правила цепочки к вычислению значений градиента нейронной сети приводит к алгоритму, который называется обратным распространением ошибки
Обратное распространение — это способ использования производных простых операций (таких как сложение, relu или тензорное произведение) для упрощения вычисления градиента произвольно сложных комбинаций этих операций.
Обратное распространение – это систематический метод для обучения многослойных искусственных нейронных сетей.
При обучении предполагается, что для каждого входного вектора существует парный ему целевой вектор, задающий требуемый выход. Вместе они называются обучающей парой.
Обучение сети обратного распространения требует выполнения следующих операций:
1.Выбрать очередную обучающую пару из обучающего множества; подать входной вектор на вход сети.
2.Вычислить выход сети.
3.Вычислить разность между выходом сети и требуемым выходом (целевым вектором обучающей пары).
4.Подкорректировать веса сети так, чтобы минимизировать ошибку.
5.Повторять шаги с 1 по 4 для каждого вектора обучающего множества до тех пор, пока ошибка на всем множестве не достигнет приемлемого уровня.
На шаги 1 и 2 можно смотреть как на «проход вперед», так как сигнал распространяется по сети от входа к выходу.
Шаги 3, 4 составляют «обратный проход», здесь вычисляемый сигнал ошибки распространяется обратно по сети и используется для подстройки весов.
TODO – тут много матана, сложновое
Глубокое обучение в технологиях компьютерного зрения. Сверточные нейронные сети.
Сверточные нейронные сети — модели, используемые для распознавания образов. Достоинство СНС - использование небольшого объема обучающих данных.
полносвязные слои изучают глобальные шаблоны в пространстве входных признаков (всё изображение)
сверточные слои (используются в СНС) изучают локальные шаблоны (например, части изображений)
1 )
шаблоны, которые изучают СНС - инвариантные
в отношении переноса. После изучения
шаблона в правом нижнем углу картинки
СНС сможет распознавать его и в левом
верхнем углу. Полносвязной пришлось бы
изучать шаблон заново, появись он в
другом месте. Это увеличивает эффективность
СНС
)
шаблоны, которые изучают СНС - инвариантные
в отношении переноса. После изучения
шаблона в правом нижнем углу картинки
СНС сможет распознавать его и в левом
верхнем углу. Полносвязной пришлось бы
изучать шаблон заново, появись он в
другом месте. Это увеличивает эффективность
СНС
2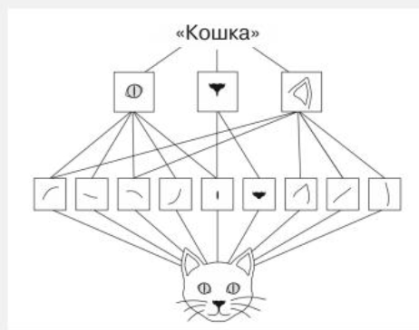 )
СНС могут изучать пространственные
иерархии шаблонов. Первый слой будет
изучать небольшие локальные шаблоны,
такие как края, второй — более крупные
шаблоны, состоящие из признаков,
возвращаемых первым слоем, и т. д. Это
позволяет СНС эффективно изучать все
более сложные образы.
)
СНС могут изучать пространственные
иерархии шаблонов. Первый слой будет
изучать небольшие локальные шаблоны,
такие как края, второй — более крупные
шаблоны, состоящие из признаков,
возвращаемых первым слоем, и т. д. Это
позволяет СНС эффективно изучать все
более сложные образы.
Свертка применяется к трехмерным тензорам с осями высота, ширина, глубина (канал/цвет).
Операция свертывания извлекает шаблоны из своей входной карты признаков и применяет одинаковые преобразования ко всем шаблонам, производя выходную карту признаков. Выходная карта признаков также является трехмерным тензором: у нее есть ширина и высота. Ее глубина может иметь любую размерность, потому что выходная глубина является параметром слоя, и разные каналы на этой оси. Изображения можно разбить на локальные шаблоны, такие как края, текстуры и т. д.
Свертки определяются двумя ключевыми параметрами:
-размером шаблонов, извлекаемых из входных данных
-глубиной выходной карты признаков — количеством фильтров, вычисляемых сверткой.
С вертка
работает методом скользящего окна: она
двигает окно размером шаблона по
трехмерной входной карте признаков,
останавливается в каждой возможной
позиции и извлекает трехмерный шаблон
окружающих признаков (с формой
(высота_окна, ширина_окна, глубина_входа)).
вертка
работает методом скользящего окна: она
двигает окно размером шаблона по
трехмерной входной карте признаков,
останавливается в каждой возможной
позиции и извлекает трехмерный шаблон
окружающих признаков (с формой
(высота_окна, ширина_окна, глубина_входа)).
Каждый трехмерный шаблон затем преобразуется (путем умножения тензора на матрицу весов, получаемую в ходе обучения, которая называется ядром свертки) в одномерный вектор с формой (выходная глубина).
Все эти векторы затем собираются в трехмерную выходную карту с формой (высота, ширина, выходная глубина). Каждое пространственное местоположение в выходной карте признаков соответствует тому же местоположению во входной карте признаков (например, правый нижний угол выхода содержит информацию о правом нижнем угле входа).
Сверточные нейронные сети. Эффект границ. Шаг свертки.
См предыдущий вопрос
Эффекты границ и дополнение

Допустим, у нас есть карта 5х5. Мы можем расположить в ней шаблоны 3х3 так. Из-за того, что на границах нельзя будет вставить шаблон в середину пикселя, пространственный размер выходной карты уменьшится.
Чтобы получить выходную карту признаков с теми же пространственными размерами, что и входная карта, можно использовать дополнение.
Дополнение: можно добавить внешние слои к изначальному изображению, чтобы середины шаблонов можно было расположить на любом месте изначальной карты:

Шаг свертки
Ррасстояние между двумя соседними окнами является настраиваемым параметром, который называется шагом свертки и по умолчанию равен 1.

Использование шага 2 означает уменьшение ширины и высоты карты признаков за счет уменьшения разрешения в два раза.
Основные задачи в сфере компьютерного зрения.
Классификация изображений
Цель — присвоить изображению одну или несколько меток. Это может быть однозначная классификация (изображение можно отнести только к одной категории) или многозначная (изображению можно присвоить несколько меток, в зависимости от наличия на нем объектов из разных категорий.
Сегментация изображений
Цель — сегментировать, или разбить, изображение на непересекающиеся области, каждая из которых представляет некоторую категорию.
Обнаружение объектов
Цель — нарисовать прямоугольники (которые называют ограничивающими рамками) вокруг интересующих объектов на изображении и связать каждый прямоугольник с некоторым классом. Как сегментация, но с обозначением границ.
Сверточные нейронные сети. Модульность, иерархия, многократное использование
См все предыдущие вопросы про комп. Зрение и СНС.
Структуризация системы в модуль, а модули в иерархии, позволяет использовать одни и те же модули в разных местах. Этот принцип основа многих архитектур, и нейронок тоже.
Все популярные архитектуры СНС структурированы по слоям — и их слои также организованы в модулями. Большинство СНС имеют пирамидальную структуру. Число фильтров растет с глубиной слоя, а размер карт признаков уменьшается.

Архитектура VGG16: обратите внимание на повторяющиеся блоки слоев и пирамидальную структуру карт признаков
Рекурентные нейронные сети. Класс задач, решаемых рекурентными нейронными сетями.
Временные последовательности — данные, полученные измерениями через регулярные промежутки времени, например стоимость акций в конце каждого дня, почасовое потребление электроэнергии в городе. Самая частая задача - прогнозирование
Классификация — присвоение временным последовательностям одной или нескольких категорий. Например, определение по временной активности посетителя веб-сайта, является он ботом или человеком.
Обнаружение событий — определение момента наступления некоторого ожидаемого события в непрерывном потоке данных. обнаружение горячих слов – распознание в аудиопотоке заранее заданные высказывания.
Обнаружение аномалий — любых необычных событий в непрерывном потоке данных. Странная активность в корпоративной сети, например, может быть признаком действий злоумышленника. используется метод обучения без учителя, заранее неизвестно, какие события нужно будет искать.
Плотносвязанные и сверточные сети плохо подходят для обработки таких наборов данных, но с ними блестяще справляются рекуррентные нейронные сети.
Биологический интеллект воспринимает информацию последовательно, сохраняя внутреннюю модель обрабатываемого, основываясь на предыдущей информации и постоянно дополняя эту модель по мере поступления новой информации.
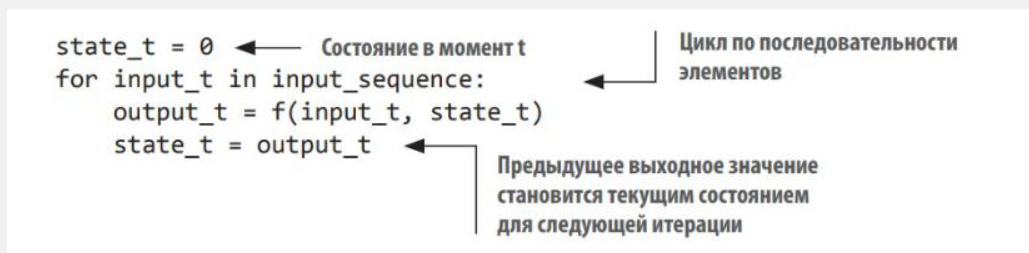
Рекуррентная нейронная сеть (RNN) использует тот же принцип: она обрабатывает последовательность, перебирая ее элементы и сохраняя состояние, полученное при обработке предыдущих элементов. RNN — это разновидность нейронной сети, имеющей внутренний цикл.
В итоге, RNN представляет собой цикл for, который повторно использует величины, вычисленные в предыдущей итерации, и не более того. При обработке нового пакета состояние сбрасывается
Состояние – текуший результат по входным признакам в ходе работы цикла. Циклу надо дать начальное состояние, чтобы она начала работать
Функция f преобразует входные данные и состояние в выходной сигнал. Паратмеризуется матрицами W и U.
Рекурентные нейронные сети. Обработка естественных языков.
См предыдущий вопрос
Подходы к обработке естественного языка на основе ML начали появляться в конце 1980-х годов. Самые ранние из них опирались на деревья решений — их целью было буквально автоматизировать разработку правил вида «если/то/иначе» по аналогии с предыдущими системами.
Затем, начиная с логистической регрессии, стали набирать обороты статистические подходы. Со временем верх взяли модели с обучаемыми параметрами.
Именно в этом суть современной обработки естественного языка. Использование ML и больших наборов данных дает компьютерам возможность не понимать язык, что является более высокой целью, а принимать фрагмент данных на естественном языке и возвращать что-то полезное.
Например, определять:
- тему текста (задача классификации текста);
- наличие в тексте наперед заданных слов (фильтрация содержимого);
- эмоциональную окраску текста (анализ эмоциональной окраски);
- следующее слово в незаконченном предложении (моделирование языка);
- то же самое выражение на немецком языке (перевод);
- формулировку основной идеи в одном абзаце (обобщение, семантический анализ) и т. д.
Модели глубокого обучения, как дифференцируемые функции, могут обрабатывать только числовые тензоры: они не принимают на входе необработанный текст. Процесс преобразования текста в числовые тензоры называется векторизацией.
Процессы векторизации текста бывают разных видов и форм, но все протекают по одному шаблону:
сначала текст стандартизируется, чтобы упростить его обработку: например, все символы преобразуются в нижний регистр или из текста удаляются знаки препинания;
затем текст разбивается на единицы (называемые токенами) — символы, слова или группы слов; данный процесс называется токенизацией;
после этого каждый токен преобразуется в числовой вектор, обычно путем индексации всех токенов, присутствующих в данных.
Обработка естественных языков. Обучение «последовательность в последовательность».
Естественный язык – языки общения людей. Они формировались постепенно, эволюционно, из-за этого содержат много противоречивых правил, в отличие от строгих искусственных.
Записать все правила языка алгоритмов не получалось однозначным, из-за природы языка, но кучу времени за неимением альтернатив работало. Требовалась консультация лингвистики, после можно стало обращаться в основном к частотным методам Вопросы, решающее ии: - можно ли искать правила в массиве данных, вместо того, чтобы придумывать их - можно ли автоматизировать процесс поиска правил языка
Решение ИИ позволяет не понимать язык, а просто понимать параметры конкретной входной фразы. Например: определение темы, фильтрация, эмоциональная окраска, перевод, поиск смысла.
Векторизация – подготовка данных. Стандартизация –удаление лишних символов, привода к одному регистру. Токенизация, Токены преобразуются в числовые векторы
Отдельная сложность в кодировании порядка слов: 1. Мешок слов – отбросить порядок
2. Рекурентные модели – обработка слов по одному в порядке следования
3.Гибридный порядок – архитектура не зависит от порядка, но учитывает информацию о положении слов
2 и 3 – модели последовательностей – входные слова преобразуются в целочисленные индексы. Все отображается в вектор. Последовательности векторов передаются в стек слов, в котором ищутся коррелирующие признаки из соседних векторов.
Обучение последовательность в последовательность – перевод, обобщение, чат боты, генерация текста.
Генеративное глубокое обучение. Класс задач, решаемых с помощью генерации данных.
Генеративное обучение – ИИ для создания проектов
Модели машинного обучения могут изучать скрытое статистическое пространство изображений, музыки и литературных произведений, а затем, основываясь на образах из этого пространства, создавать новые произведения с характеристиками, схожими с теми, что модель видела в обучающих данных. Языковые модели- см следующий вопрос
Художественная обработка – см дальше
Генеративное глубокое обучение. Языковая модель.
Успешное применение методов генерации последовательностей c помощью рекуррентных сетей начало приобретать широкую известность только в 2016 году, хотя методы были придуманы еще в 1997 (алгоритм LSTM)
Универсальный способ генерации последовательностей – обучение модули для прогнозирования следующего токена или следующих нескольких токенов в последовательности, опираясь на предыдущие токены.
Алгоритмы выбора токена:
Жадный выбор - выбирается наиболее вероятный символ. Приводит к получению повторяющихся, предсказуемых строк, несвязных предложений.
Стохастический выбор – как жадный, но у каждого слова есть вероятность выбора. Нет возможности изменить вероятность слов по ходу генерации. Выбор вероятности разных слов (поставить всем равную или разную вероятность, увеличивать или уменьшать энтропию) изменяет предсказуемость, интересность генерации.
Температура - энтропия распределения вероятностей, используемая для выбора: определяет степень необычности или предсказуемости выбора следующего символа
Выбор следующего токена требует баланса между мнением языковой модели и случайностью. Это регулируется температурой.
Генерация текста. Стратегии выбора.
См предыдущий вопрос.
Генеративное глубокое обучение. Художественная обработка изображений.
DeepDream — это метод обработки изображений, основанный на СНС. Реализован google в 2015 году и выдавал психодел
Нейронная передача стиля (2015) - применение стиля изображения-образца к целевому изображению при сохранении содержимого.

Идея передачи стиля, тесно связанная с созданием текстур, давно вынашивалась в сообществе людей, увлеченных обработкой изображений, прежде чем воплотилась в алгоритм нейронной передачи стиля в 2015 году. Однако, как оказалось, реализации передачи стиля, основанные на глубоком обучении, не имеют аналогов среди прежних достижений, использовавших классические методики компьютерного зрения, и потому они породили удивительный бум в сфере художественных приложений компьютерного зрения.
Генетические алгоритмы. Основные понятия.
Генети́ческий алгори́тм — экспериментальный алгоритм поиска, для решения задач оптимизации и моделирования путём случайного подбора, комбинирования искомых параметров с использованием механизмов, эволюции (наследование, мутации, отбор).
Оператор «скрещивания», производит операцию рекомбинации решений-кандидатов
Функция успешности – функция приспособленности (определяет выживаемость)
Алгоритм основан на нейронной сети. Генетически подбираются веса (через мутации, отбор, наследование). Мутируют отдельные веса.
Сопоставление весов генам – кодирование
Набор параметров (весов) для решения – генотип
Само конкретное решение – особь, фенотип
Общая схема, по которой работает подавляющее большинство эволюционных алгоритмов, выглядит следующим образом:
1. Задаем схему кодирования решения. Определяем, как гены будут задавать веса нейросети.
2. Создаем исходную популяцию решений, случайно задав значения генов. Пусть будет 100 решений.
3. Каждую особь-нейросеть популяции тестируем. После теста при помощи функции приспособленности рассчитываем приспособленность каждой особи.
4. Формируем следующее поколение решений. Для каждого потомка выбираем двух родителей из предыдущего поколения. Родители выбираются пропорционально приспособленности: чем лучше решение, тем выше вероятность того, что он примет участие в размножении.
5. Перемешиваем гены родителей и вносим в них небольшие мутации.
6. Теперь у нас есть следующее поколение, для его тестирования переходим к п. 3.
7. Отслеживаем, насколько хорошо решается поставленная задача.
