1.ИИ. Определения ИИ. История развития ИИ

ИИ — это способность компьютера обучаться, принимать решения и выполнять действия, свойственные человеческому интеллекту.

Понятие дал Джон Маккарти в 1956 году: «под интеллектом в пределах этой науки понимается только вычислительная составляющая способности достигать целей в мире».

Идеи создания подобия ИИ впервые развил Р. Луллий, который в XIV в. пытался создать машину для решения различных задач на основе всеобщей классификации понятий.

В XVIII и. Г.Лейбниц и Р.Декарт независимо друг от друга развили эту идею,

предложив универсальные языки классификации всех наук, только в теории. На практике реализовать получилось только после создания ЭВМ и появления новой науки кибернетики.

История ИИ начинается в середине XX века. Предпосылки: см вопрос 2

В 1950 году Алан Тьюринг - статья «Может ли машина мыслить?» - описание теста Тьюринга. Подробнее: вопрос 3

Россия:

С.Н. Корсаков (1787—1853) исследовал усиление естественного интеллекта. В 1832 году С. Н. Корсаков опубликовал описание пяти устройств, «интеллектуальных машин», для частичной механизации умственной деятельности в задачах поиска,

сравнения и классификации. Впервые в истории информатики применил перфокарты

В СССР работы начались в 1960-х. Вопросы, связанные с обучением конечных автоматов.

В 1968 году вышла книга философа Э. В. Ильенкова «Об идолах и идеалах», в которой обосновывалась невозможность создания машины умнее человека.

был создан Научный совет по проблеме «ИИ»

10 октября 2019 года В. В. Путин своим указом утвердил национальную стратегию развития ИИ в России до 2030 года.

В ноябре 2019 года Сбербанк, «Газпром нефть», «Яндекс», Mail.ru Group, МТС

и Российский фонд прямых инвестиций (РФПИ) создали Альянс в сфере

ИИ (к лету 2023 года в состав Альянса вошли также Уралхим, Русагро, Сибур и Северсталь).

Направления:

Нейрокибернетика – моделирование структур подобных мозгу (нейросети);

кибернетика «черного ящика» - главное чтобы на входной импульс была реакция подобная человеческому мозгу.

2.Предпосылки развития науки ИИ

Также см вопрос 1

- среди философов давно шли споры о природе человека и процессе познания мира,

- нейрофизиологи и психологи разработали ряд теорий относительно работы

человеческого мозга и мышления,

- экономисты и математики задавались вопросами оптимальных расчётов и

представления знаний о мире в формализованном виде;

- зародился фундамент математической теории вычислений — теории алгоритмов — и были созданы первые компьютеры.

1. Отличительной чертой новых ЭВМ является их максимальная приближенность к пользователю, освобождение пользователя от программирования решения задач.

2. Из-за внедрениея ЭВМ во все сферы человеческой жизни, развитием локальных - изменение стиля человеческого общения

3. 3. В роботизированных производствах нет необходимости в создании «человеческих условий» для исполнителей

ИС позволят ученым решать проблемы, на решение которых не хватает сейчас жизни нескольких поколений.

3.Парадигмы ИИ. Тест Тьюринга

Две парадигмы:

1. Результативно-ориентированный: теория вероятности, статистика, теория игр. Важен конечный результат

2. Имитационно-ориентированный: основа на человеческом мышлении и поведения. Важна естественность процесса

Возможные вопросы: действительно ли программы двух парадигм обладают интеллектом; если да, то какая из двух программ умнее.

Что есть мера интеллекта — способность выигрывать или человекоподобное поведение?

Тест Тьюринга – вариант решения вопросы

Поведение машины будет считаться интеллектуальным, если опросчик не сможет отличить ее от человека.

Программа DOCTOR (1960-е). Имитации поведения психиатра Рогерианской школы психоанализа, проводящего психологический опрос. Измененные выражения возвращались на экран пользователя в виде ответных реплик. Например, в ответ на выражение “Я сегодня устал” программа DOCTOR выдавала сообщение: “Как вы думаете, из-за чего вы сегодня устали?” Если программа не могла распознать сообщение, она просто выводила малозначащую общую фразу, например “Продолжайте, продолжайте...” или “Очень интересно”. Пользователи чувствовали контакт с личностью, тест Тьюринга в какой-то степени прошелся.

Тест Тьюринга оценивает уровень соответствия поведения

машины по отношению к поведению человека. Тьюринг предполагал, что к

2000 году машины смогут с 30-процентной вероятностью продержаться пять

минут. Эта догадка оказалась на удивление точной.

4. Подходы к созданию интеллектуальных систем.

• нисходящий, семиотический — создание экспертных систем, баз знаний и систем логического вывода, имитирующих высокоуровневые психические процессы: мышление, рассуждение, речь, эмоции, творчество и т. д.;

• восходящий, биологический — изучение нейронных сетей и эволюционных вычислений (генетические алгоритмы), моделирующих интеллектуальное поведение на основе биологических элементов, а также создание соответствующих вычислительных систем, таких как нейрокомпьютер или биокомпьютер.

Интуитивный подход

ИИ будет проявлять поведение, не отличающееся от человеческого. Обобщение подхода теста Тьюринга. Подробнее: вопрос 3

Ответвление - ИИ возникнет тогда, когда машина будет способна чувствовать и творить.

Логический подход

Основан на моделировании рассуждений. Основа - логика. Может быть проиллюстрирован применением для этих целей языка и системы логического программирования. Программы, записанные на языке Пролог, представляют наборы фактов и правил логического вывода без жесткого задания алгоритма как последовательности действий, приводящих к необходимому результату.

Агентно-ориентированный подход

1990-е. Интеллект — это вычислительная часть способности достигать целей. Сама машина будет интеллектуальным агентом, воспринимающим мир с помощью датчиков, и способной на мир с помощью исполнительных механизмов. Важны методы, которые помогут интеллектуальному агенту выживать в окружающей среде при выполнении его задачи. Здесь большее значение уделяется изучению алгоритмов поиска пути и принятия решений.

Гибридный подход

синергийная комбинация нейронных и символьных моделей. Например, экспертные правила умозаключений могут генерироваться нейронными сетями, а порождающие правила получают с помощью статистического обучения.

Символьное моделирование мыслительных процессов

Одна из самых развитых областей в современном ИИ.

Моделирование рассуждений подразумевает создание символьных систем, на входе которых поставлена некая задача, а на выходе требуется её решение. Как правило, предлагаемая задача уже формализована, то есть переведена в математическую форму, но либо не имеет алгоритма решения, либо он слишком сложен, трудоёмок и т. п. В это направление входят: доказательство теорем, принятие решений и теория игр, планирование и диспетчеризация, прогнозирование.

5. Направления развития ИИ

Работа с естественными языками

Анализ возможностей понимания, обработки и генерации текстов на «человеческом» языке. Цель - быть в состоянии приобрести знание самостоятельно, читая существующий текст, доступный по Интернету. Некоторые прямые применения обработки естественного языка включают информационный поиск и машинный перевод.

Представление и использование знаний

Производство, систематизация знаний из данных. Используют базы знаний для получения достоверных заключений по какой-либо проблеме. Существуют различные подходы к решению этой проблемы, в том числе — на основе нейросетевой технологии.

ML

было центральным с самого начала развития ИИ. В 1956 году, Рей Соломонофф написал отчёт о вероятностной машине, обучающейся без учителя, назвав её: «Индуктивная машина вывода».

Обучение без учителя — позволяет распознать образы во входном потоке. Обучение с учителем включает также классификацию и регрессионный анализ. Классификация используется, чтобы определить, к какой категории принадлежит образ. Регрессионный анализ используется, чтобы в рядах числовых примеров входа/выхода обнаружить (закономерность) непрерывную функцию, на основании которой можно было бы прогнозировать выход.

При обучении агент вознаграждается за хорошие ответы и наказывается за плохие. К области ML относится большой класс задач на распознавание образов.

Биологическое моделирование ИИ

ИИ не обязаны повторять процессы, присущие биологическим системам. Нейронные сети используются для решения нечётких и сложных проблем, таких как распознавание геометрических фигур или кластеризация объектов. Генетический подход основан на идее, что некий алгоритм может стать более эффективным, если позаимствует лучшие характеристики у других алгоритмов («родителей»).

Робототехника

чтобы манипулировать объектами, выполнять навигацию с проблемами локализации (определять местонахождение, изучать ближайшие области) и планировать движение (как добраться до цели).

Машинное творчество

Природа человеческого творчества ещё менее изучена, чем природа интеллекта. Теория решения изобретательских задач, предложенная в 1946 году Г. С. Альтшуллером, положила начало исследованиям машинного творчества.

6. Области применения ИИ

Можно просто из 5 вопроса взять

Финансы – алгоритмическая торговля, аукционы, исследования рынка

Государственное управление – военное дело

Промышленность – робототехника, автоматизация

Медицина – анализы, обработчики, уход, консультации

Техпорт

Транспорт

7. ИС. Основные понятия и определения. Структура интеллектуальной системы.

ИС – техническая или программная система, способная решать «творческие» задачи, принадлежащие конкретной области, знания о которой хранятся в памяти системы.

Структура:

-База знаний,

-механизм вывода решений,

-интеллектуальный интерфейс.

Признаки:

− развитые коммуникативные способности (диалог с юзером на естественном языке);

− умение решать сложные плохо формализуемые задачи (требуют алгоритма, но неопределенные, исходные данные могут быть динамичны);

− способность к самообучению;

− адаптивность (способность к самоизменению системы).

БЗ — БД, содержащая правила вывода и информацию о знаниях в некоторой  области. В самообучающихся системах БЗ содержит также информацию, с прошлых итераций решения.

Современные БЗ работают совместно с системами поиска и извлечения информации. Для этого требуется некоторая модель классификации понятий и определённый формат представления знаний.

Онтология – иерархический способ представления знаний в БД

8. Модели и методы знаний. Структуры памяти ЭВМ. Информационные структуры для хранения данных.

СМ вопрос 7

---------

Информация в ЭВМ: процедурная – команды, которые выполняет ЭВМ

Декларативная – данные, которыми оперирует программа

Где хранить: регистры процессора, кэш-память, RAM, внешняя память.

Данные хранятся в виде машинных слов одинаковой длины

--------

Информационные структуры: появилась возможность хранить вектора и матрицы, списки, иерархические структуры (графы и деревья), мапы. БД и СУБД.

9. Модели представления данных.

БД в 70х: реляционные, сетевые (графы) и иерархические (графы)

Интенсиональные представления – схемы БД и системная инфа

Экстенсиональные представления - данные

Модели данных – средства представления исходных данных и их взаимосвязи.

В сетевой модели связи - “многие к одному”:

- обработка может быть начата с записи любого типа;

- от извлеченной записи возможны переходы как к ее подчиненным записям, так и к тем, которым она подчинена; - подчиненная запись может иметь только одного владельца, что делает невозможным представление связей типа “многие ко многим”

Пример иерархической структуры - генеалогическое древо. Древовидная структура может существовать лишь тогда, когда для каждого объекта указан только один исходный.

10. Концепция знаний.

Знания это выявленные закономерности предметной области (принципы, связи, законы). Хранятся в БЗ (см. вопросы 7-9)

Классификация:

поверхностные знания о видимых взаимосвязях между событиями и фактами

глубинные абстракции, аналогии, схемы, отображающие структуру и процессы

знания объединяют в себе многие черты процедурной и декларативной информации.

Особенности знаний в ЭВМ: Внутренняя интерпретируемость – возможность найти знание по имени/id

Структурированность – каждая информационная единица может быть включена в состав любой другой, и из каждой информационной единицы можно выделить некоторые ее составляющие. Это позволяет устанавливать между отдельными ИЕ отношения типа «часть-целое», «род-вид» или «элемент-класс»

Связность – возможность установления отношений (типа 1к1, многок1 и тп).

Семантическая метрика На множестве информационных единиц в некоторых случаях полезно задавать отношение, характеризующее ситуационную близость информационных единиц, т.е. силу ассоциативной связи между ИЕ. Такое отношение дает возможность выделять в информационной базе некоторые типовые ситуации (например, «покупка», «перевод студента» и т.п.).

Предметная область – это все предметы и события, которые составляют основу общего понимания имеющейся информации, необходимой для решения задачи.

Гипотетически предметная область представляется состоящей из реальных или абстрактных объектов, которые называются сущностями.

Сущности предметной области находятся в определенных отношениях друг к другу (ассоциациях), которые также можно рассматривать как сущности и включать в предметную область.

Отношения между сущностями выражаются с помощью суждений.

11. Модели представления знаний. Логические и сетевые модели.

См вопрос 10

----

Логические:

Есть множество объектов (алфавит) и функция определения этого объекта в алфавите

В множестве синтаксически правильных совокупностей подмножество А (аксиомы). Существует процедура П(А), которая выводит принадлежность элемента к множеству А.

В - множество правил вывода. Применяя их к элементам А, можно получать новые синтаксически правильные совокупности, к которым снова можно применять правила из В. Так формируется множество выводимых совокупностей. Если имеется процедура П(В), с помощью которой можно определить для любой совокупности, является ли она выводимой, то система называется разрешимой. 

Для знаний, входящих в БЗ, можно считать, что А образуют все данные в БД, внесенные извне, а с помощью правил вывода из них выводятся новые производные знания. Система представляет собой генератор новых знаний = множество B. Можно хранить в базе знания, из множества А, а все остальные знания получать из них по правилам вывода

Пример:

Алфавит – стол и стул. Аксиома «за столом сидеть можно» и «за стулом сидеть нельзя». В задаче «определить можно ли сидеть за объектом» определяем объект как стол с помощью функции принадлежности и решаем «за конкретно этим объектом (а он стол) сидеть можно»

Использование: доказательство теорем. Прямая цепочка вывода – берем аксиому, из нее вывод, из нее цепочку вывода, из нее утверждение

Обратная цепочка вывода – придумываем гипотезу, ищем под нее аксиому. Популярно в логических моделях.

-----

Сетевые:

формально можно задать в виде Н=<I, C1, C2,, … , Cn ,Г>

I - множество информационных единиц.

C1, C2,, … , Cn – множество типов связей между ИЕ.

Отображение Г задает между ИЕ, входящими в I, связи из заданного набора типов связей.

Типы семантических сетей:

Классифицирующие сети - отношения структуризации. Можно в БЗ вводить иерархические отношения между ИЕ.

Функциональные сети - функциональные отношения. Их часто называют вычислительными моделями, т.к. они позволяют описывать процедуры «вычислений» одних информационных единиц через другие.

В сценариях используются отношения типа «средство-результат», «орудие-действие» и т.п. Часто отдельные события идут вместе.

Семантическая сеть – это ориентированный граф, вершины которого – понятия, а дуги – отношения между ними.

Если в сетевой модели допускаются связи различного типа, то ее обычно называют семантической сетью.

Понятия - объекты (множество I). Отношения – это связи типа «имеет частью», «это», «принадлежит» и т.п. (отображение Г).

Поиск решения в БЗ семантической сети сводится к поиску фрагмента сети, соответствующей вопросу.

12. Модели представления знаний. Продукционные и фреймовые модели.

Продукционная модель, или модель, основанная на правилах, позволяет представить знания в виде предложений типа

ЕСЛИ (условие), ТО (действие). По условию – поиск в БЗ. Действие – выполняется при условии поиска (часто является тоже условием).

БЗ состоит из набора правил. Программа - машина вывода. Чаще всего вывод бывает прямой (от данных к поиску цели) или обратный (от цели для ее подтверждения – к данным). Данные – это исходные факты, на основании которых запускается машина вывода – программа, перебирающая правила из базы.

Ядра (продукции) могут быть детерминированными (Если А то точно Б) и недетерминированными (Если А то возможно Б)

Недетерминированность можно описать

- стохастически: (Если А то с вероятностью p Б)

- Лингвистически (Если А то скорее всего Б, реже В) (когда вероятность не ясна)

--------

Фрейм выглядит примерно так:

( Имя фрейма:

Имя слота1 (значение слота1),

…

Имя слота N (значение слота N)

)

В слоте может быть что угодно (числа или математические соотношения, тексты на естественном языке или программы, правила вывода или ссылки на другие слоты данного фрейма или других фреймов).

Пример:

13. Методы работы со знаниями. Механизм вывода решений

Группы методов:

приобретение знаний - выявление знаний из источников и преобразование их в нужную форму, а также перенос в БЗ

пополнение знаний;

обобщение и классификация знаний.

Субьективные системы – эмпирические знания системы, экспертные знания

Извлечение субъективных знаний опирается на их репрезентативность

Для извлечения знаний у эксперта инженер по знаниям может воспользоваться

протокольный анализ - записи «мыслей вслух» эксперта во время решения проблемы;

интервью – самый важный;

игровая имитация профессиональной деятельности – наблюдаем и записываем.

Подходы пополнения знаний:

-модели «здравого смысла»;

-сценарии;

-подход, опирающийся на идею о том, что физические закономерности внешнего мира могут быть описаны в рамках специальных логик.

Во всех подходах основа – законы формальной логики, транзитивность, обобщение

14. Экспертные системы. Структура экспертных систем.

Экспертная система- система строится экспертами и сама становится экспертом, помогающим принимать решения.

Первые ЭС – медицинские базы знаний для помощи в выборе лечения

1.ЭС ориентированы на решение широкого круга задач в неформализованных областях

2.С помощью ЭС специалисты, не знающие программирования, могут самостоятельно разрабатывать интересующие их приложения

3.ЭС достигают результатов, не уступающих, а иногда и превосходящих возможности экспертов, не имеющих «под рукой» экспертную систему.

Формально копилот и аналоги это ЭС

Шакальная структура:

Решатель (машина вывода) программа, моделирующая ход рассуждений эксперта на основании знаний, имеющихся в базе знаний.

Подсистема объяснений - программа, позволяющая пользователю получить ответы на вопросы «Как была получена та или иная рекомендация?» и «Почему система приняла такое решение?».

15. Экспертные системы. Классификация экспертных систем.

См вопрос 14

1.Экспертные системы интерпретации данных. Под интерпретацией понимается определение смысла данных, результаты которого должны быть согласованными и корректными. Например, система диагностики легких.

2. Диагностика. обнаружение отклонения от нормы: неисправность оборудования, и заболевания живых организмов, и всевозможные природные аномалии. Например, предиктивная диагностика.

3.Мониторинг непрерывная интерпретация данных в реальном масштабе времени и сигнализация о выходе тех или иных параметров за допустимые пределы.

4.Проектирование подготовка спецификаций (чертежей, пояснительных записок и т.д.) на создание «объектов» с заранее определенными свойствами.

5.Прогнозирующие системы Например, предсказание погоды (WILLARD)

16. Экспертные системы. Этапы разработки экспертных систем.

См вопросы 14-15

выбор проблемы – определение предметной области, задачи, нахождение экспертов, анализ расходов, прибыли и прочий менеджмент;

разработка прототипа – уточнение проблемы, извлечение знаний, структурирование знаний, формализация знаний, реализация, тестирование;

доработка до промышленной системы;

оценка;

стыковка;

поддержка.

17. Инструментальные средства создания интеллектуальных систем. Решающие деревья.

Решающее дерево — решение задачи обучения с учителем, основанное на том, как решает задачи прогнозирования человек. В общем случае — это k-ичное дерево с решающими правилами в узлах и некотором заключении о целевой функции в листовых вершинах (прогнозом). Решающее правило — некоторая функция от объекта, позволяющая определить, в какую из дочерних вершин нужно поместить рассматриваемый объект.

Требования к системе: - набор состояний (ситуаций). Стартовое, целевое, промежуточные

- набор порождений (ходов) – операция перевода из 1 состояния в другое

- система контроля (выбирает порождение) – можно сказать программа

- граф состояний (граф переходов состояний между друг другом по порождениям)

 задача системы контроля состоит в нахождении пути по графу состояний.

дерево поиска, - часть графа состояний, исследованной системой контроля (сеть петри)

Другие системы:

Нейронная сеть — это метод в искусственном интеллекте, который учит компьютеры обрабатывать данные таким же способом, как и человеческий мозг. Это тип процесса ML, называемый глубоким обучением, который использует взаимосвязанные узлы или нейроны в слоистой структуре, напоминающей человеческий мозг. Он создает адаптивную систему, с помощью которой компьютеры учатся на своих ошибках и постоянно совершенствуются.

Генети́ческий алгори́тм — эвристический алгоритм поиска, используемый для решения задач оптимизации и моделирования путём случайного подбора, комбинирования и вариации искомых параметров с использованием механизмов, аналогичных естественному отбору в природе. Является разновидностью эволюционных вычислений, с помощью которых решаются оптимизационные задачи с использованием методов естественной эволюции, таких как наследование, мутации, отбор.

18. Сетевые модели. Сети Петри. Основные понятия и определения.

Двудо́льный граф – граф в котором вершины можно разделить на две группы, внутри группы нет соединений.

мультиграф – это граф, в котором существуют вершины объединенные несколькими дугами

Сеть Петри (СП) - это двудольный ориентированный мультиграф N = (P, T, I, O, µ0), где:

P - конечное непустое множество элементов, называемых позициями;

T - конечное непустое множество элементов, называемых переходами; \

I: PT{0,1,2...} и O: PT{0,1,2...} - функции инцидентности;

µ0 : P{0,1,2...} - начальная разметка.

n =P- мощность множества P,

m =T - мощность множества T.

Кратность дуги, соединяющей позицию pi с переходом tj = I(pi, tj). Кратность дуги, соединяющей переход tj с позицией pi =  O(pi, tj). (см матричный). Кратность - возможность дублирования дуги.

Если I(pi, tj) > 0, то позицию pi называют входной к переходу tj

Множество входных переходов к pi = pre(pi)={t | O(pi, tj) > 0},

Множество выходных позиций к tj - = post(tj)={p | O(pi, tj) > 0}.

Головная позиция, хвостовая позиция

Элементарная сеть = N = (P, T, I, O, µ0 ), где  T={t}; P={p',p''}; pre(t)={p'}, post(t) = {p''}; µ0 = (0,0).

Переход tj активен, если pi pre(tj): (pi ) >= I(pi, tj)

Тупиковая разметка – разметка, при которой нельзя совершить переход никуда

Если из позиции связи идут в несколько переходов, то следующую разметку можно получить активацией любого перехода

19. Сети Петри: формы представления сетей Петри, графы сетей Петри, правила функционирования сетей Петри.

Формы представления сетей Петри:

Графически - При этом позиции изображают кружками, переходы - черточками или прямоугольниками.

Матричный: I – связывает позиции и переходы. O – связывает переходы и позиции

Алгебраческая (см вопрос 22)

20. Сети Петри: дерево достижимых разметок.

См вопрос 26

21. Оценка свойств сетей Петри на основе матричных уравнений.

См вопрос 27 (анализ сети петри, матричные уравнения)

22. Алгебра сетей Петри: операции над сетями Петри.

Пример:

фф

Знак + - если две ветки соединяются в переходе. Знак доллара, если две ветки соединяются в позиции.

23. Расширения сетей Петри: ингибиторные, приоритетные, временные.

Ингибиторные

Ингибиторная сеть представляет собой СП, дополненную специальной функцией инцидентности FI:P T {0,1}, которая вводит ингибиторные дуги для тех пар (p,t), для которых FI(p,t) = 1.

Приоритетные

Спорные переходы дополняются приоритетами:

если несколько переходов готовы сработать, то срабатывает такой переход, приоритет которого не меньше приоритетов остальных готовых к срабатыванию переходов. класс приоритетных СП строго мощнее СП и равномощен классам машин Тьюринга и Минского.

Временные

расширение СП позволяет отразить в модели временные параметры системы

фактор времени учитывается путем введения задержки между моментом изъятия меток из входных позиций сработавшего перехода и моментом помещения меток в выходные позиции данного перехода.

24. Способы описания сетей Петри.

См вопрос 19

25. Методы анализа сетей Петри. Задачи анализа.

Известно, что если позиция безопасна, то число меток в ней равно 0 или 1.

Безопасность - это частный случай более общего свойства ограниченности.

Наличие или отсутствие тупиковых ситуаций. Тупики в реальных системах возникают при распределении ресурсов между взаимодействующими процессами.

Задача достижимости формулируется следующим образом:

для СП N с начальной разметкой m0 и конечной разметкой m' определить существует ли последовательность переходов ν , срабатывание которых переводит разметку m0 в m’ .

Задача достижимости является основной задачей анализа СП. Многие другие задачи анализа можно сформулировать в терминах задачи достижимости.

Методы:

1 - построение дерева достижимых разметок,

2 – метод, основанный на решении матричных уравнений.

26. Методы анализа сетей Петри. Дерево достижимых разметок.

См предыдущий вопрос

Множество достижимых разметок можно представить в виде дерева достижимости (ориентированный граф), в котором обозначены конкретные состояния, и переходы между ними (если они возможны).

Из-за наличия циклов/большого количества ветвлений граф может получиться большим. Поэтому есть упрощающие приемы.

Разметки из которых нет переходов – терминальные

Разметки, которые уже встречались ранее – дублирующие. Рассматривать их дальше не обязательно, так как путь из нее уже рассмотрен ранее.

Разметки, в которых количество меток увеличивается приведут к бесконечному циклу (внутренние неограниченные)

Внутренние метки – между другими

Граничные метки – временные метки во время работы алгоритма. Текущая конечная метка. После рассмотра станет меткой другого типа.

Когда все метки становятся терминальными, дублирующими или внутренними, работа алгоритма заканчивается.

27. Методы анализа сетей Петри. Анализ на основе матричных методов.

Показано, что если СП живая и ограниченная, то она должна быть последовательной и инвариантной. Данные свойства недостаточны для утверждения живости и ограниченности СП. Однако их полезно проверить исходя из матриц инцидентности, так как если одно из этих свойств не подтверждается, то можно заключить, что описываемая система содержит некоторые недоработки.

Инвариантные и последовательные сети Петри . Введем в рассмотрение матрицу С, которая получается следующим образом:

C = O - I .

Пусть размерность С равна n ´ m , где m и n мощности множеств P и T .

Рассмотрим матричные уравнения :

C * x = 0 ; (1)

y * C = 0 , (2)

где x и y - векторы, размерность которых равна n и m соответственно.

Вектор у, удовлетворяющий решению уравнения (1) и все элементы которого положительны, называется р-цепью; р-цепь, все элементы которой больше нуля, называется полной р-цепью.

Анaлогично на основе уравнения (2) определяются понятия t-цепи и полной t-цепи.

СП, для которой существует полная р-цепь, называется инвариантной. СП, для которой существует полная t-цепь, называется последовательной .

28. Проектирование сложных вычислительных структур. Структурный подход.

Аппарат СП широко используется при проектировании и верификацией сложных систем, с сетевыми моделями, асинхронностью, многопроцессорностью

При использовании структурного подхода выделяют следующие основные этапы:

1) описание функций, которые должна выполнять система;

2) выработка ряда гипотез, из которых будет состоять система (декомпозиция);

3) формирование из данных гипотез (подсистем) законченных структур-кандидатов (синтез);

4) анализ каждой структуры для определения характеристик, для сокращения числа структур-кандидатов и выбора окончательной структуры.

Множество структур-кандидатов - метрическое пространство, на котором можно ввести различные шкалы, количественно оценивающие каждую СП-модель. Это позволяет выбрать лучшие структуры по заданным критериям

Проблема в NP-сложности задачи получения множества альтернативных вариантов, что существенно ограничивает практическое использование данного подхода.

Одним из подходов при решении проблем NP-сложности является ввод ряда ограничивающих условий (построение базы знаний), позволяющих уменьшить число рассматриваемых вариантов, и тем самым снизить сложность решаемой задачи.

Одним из методов достижения высокой производительности систем обработки данных реального времени является использование процессорных матриц – специализированных вычислительных структур, состоящих из множества относительно простых устройств (процессорных элементов), объединённых в однородные параллельные системы.

29. Матричные структуры. Преимущества матричных структур.

Процессорные матрицы – специализированные вычислительных структуры, состоящие из множества относительно простых устройств (процессорных элементов), объединённых в однородные параллельные системы.

Матричный процессор – процессор специально для операций с матрицами.

Матричные процессоры эффективные устройства, позволяющие решать определенный круг задач с существенным ускорением. Но они эффективны только для определенного круга задач. Дальше см следующий вопрос

30. Примеры проектирование структур матричных процессоров на основе проекций процессорных элементов.

См вопрос 29

Рассмотрим умножение матрицы 3*3.

для организации задержек с целью одновременной подачи элементов матриц А и В на ПЭ элементы матрицы подаются со смещением.

Например, в результате 2 тактов, будет такой промежуточный результат:

На 5 итерации:

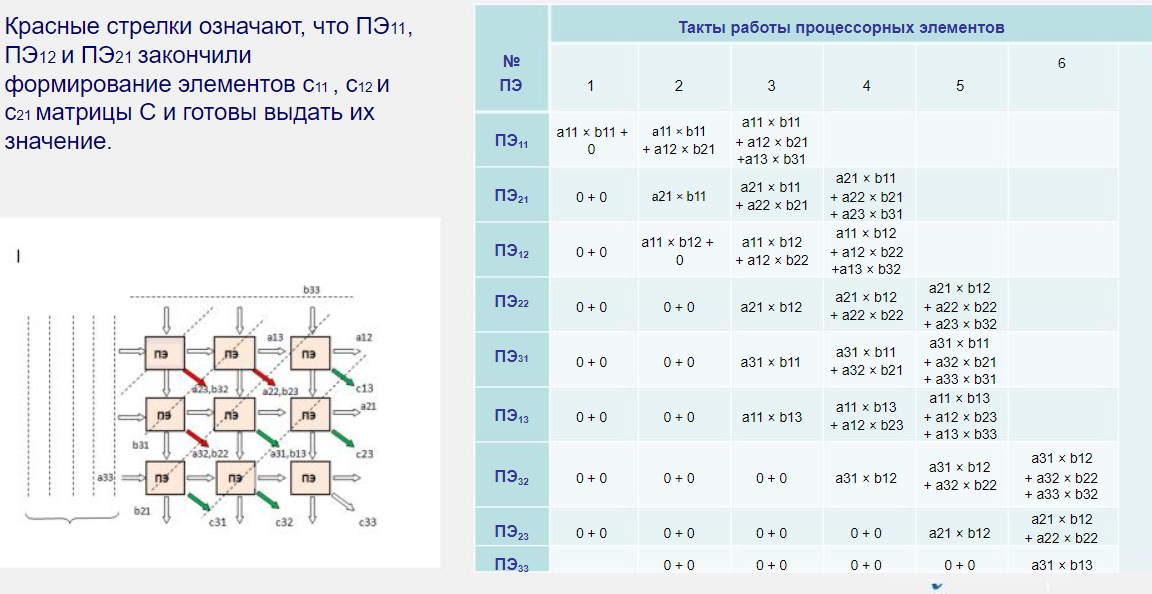
Матрицы 3*3 можно умножить на таком процессоре за 8 итераций.

31. Построение параллельных матричных систем на примере умножения двух матриц.

TODO – нихера не понятно

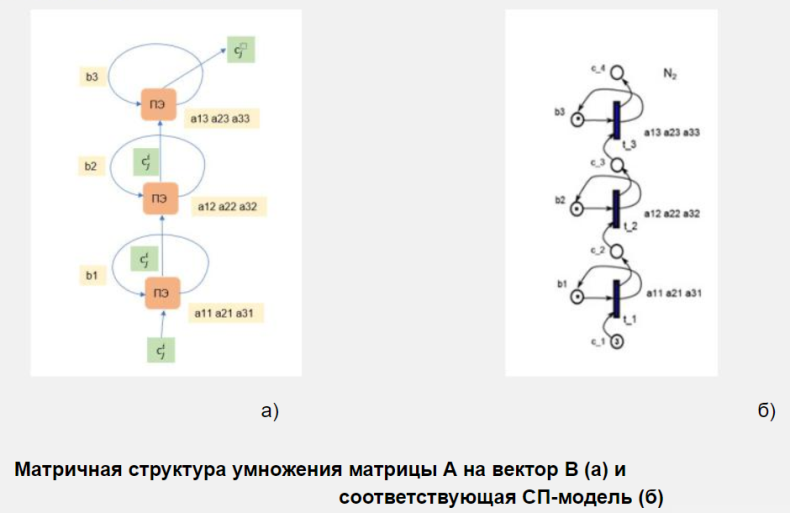
32. Анализ и синтез сп-моделей сложных систем. Декомпозиция моделей.

На первом шаге к синтезу новых моделей, мы осуществляем анализ имеющейся исходной СП-модели. Проводим декомпозицию модели с целью получения составных линейных или линейно-циклических фрагментов.

Cущность декомпозиционных методов заключается:

-в разбиении сложной системы на более простые,

-в исследовании этих простых систем,

-в объединении результатов с целью получения некоторого целостного и единого решения.

Объединение вершин СП-моделей

Для проведения анализа и синтеза сетевых моделей необходимы средства, позволяющие преобразовывать СП-модели.

СП, в которой P = {p', p''}, T={t}, p' pre(t) и p'' post(t), есть элементарная сеть.

СП, состоящую из множества элементарных сетей, будем называть

примитивной системой NPR.

Объединением переходов ti и tj (ti + tj ) является переход tij , для которого справедливо:

pre (tij ) = pre (ti ) pre (tj); post (tij ) = post (ti ) post (tj).

Объединением позиций pi и pj (pi + pj ) является позиция pij , для которой справедливо:

pre (pij) = pre (pi) pre (pj); post (pij) = post (pi) post (pj); (pij) = max ( (pi) , ( (pj)).

Разделение вершин

Делению подвергаются вершины, которые удовлетворяют следующим условиям:

|pre(t)| + |post(t)| > 2; |pre(p)| > 1 или |post(p)| > 1 .

Разделение переходов

При делении переходов нарушается синхронизация параллельно протекающих процессов, а также нарушаются заданные в СП-модели связи между последовательными процессами.

Разделение позиций. Деление головной позиции

Головную позицию можно раздробить на несколько, чтобы из каждой шел 1 переход

Разделение позиций. Деление хвостовой позиции

Хвостовую можно разбить на несколько, чтобы в каждую шел 1 переход

Деление позиции с одинаковым числом входных и выходных переходов

Если входов столько же, сколько и выходов, можно на каждый вход-выход сделать по позиции.

Деление позиции с различным числом входных и выходных переходов

Определение 5. Вертикальное деление позиции.

Если для позиции pj выполняются условия:

pre(pj) = {t11, t12,..., t1m} , post(pj) = {t21, t22,..., t2n} и

а) n > m , то позиция pj делится на позиции pj ' и pj '' , для которых справедливо:

pre(pj ') = {t11, t12,..., t1m } , post(pj') = {t21, t22,..., t2m},(pj ') = (pj ) , pre(pj '') = , post(pj '') = {t2(m+1),..., t2n},(pj '') = (pj ) ;

б) n < m, то позиция pj делится на позиции pj ' и pj '', для которых справедливо: pre(pj ') = {t11, t12,..., t1n}, post(pj') = {t21, t22,..., t2n}, (pj ') =(pj ), pre(pj '') = {t1(n+1),..., t1m}, post(pj'') = , (pj'') = (p j ) .

Разделение вершин СП-моделей

При делении позиций и переходов часто имеет смысл сохранять максимально длинную последовательность вершин. Это позволяет при синтезе новых СП-моделей, формировать дополнительные ограничения и сокращает число вариантов синтезируемых СП-моделей.

Этапы декомпозиции:

Этап 1. Построение системы ЛБФ. Выделение циклов

Построили квадратную матрицу с одинаковыми сторонами (и переходы и вершины). Единички ставим если есть переход из эл. В строке в эл. В столбце.

Делим систему на фрагменты

Этап 2. Построение примитивной системы

Примитивная система отражает состав элементов, из которых построена исходная СП-модель.

Этап 3. Построение тензорных уравнений. Типы геометрий

См следующие 2 вопроса

Этап 4. Синтез СП-моделей. Программы синтеза СП-моделей

См дальше