Расписанные билеты по ТФКП Сучкова

1. Дифференцируемость функции комплексной переменной. Условия Коши -Римана. Определение аналитической функции в области и в точке. (лек 2)

2. Аналитичность суммы степенного ряда. (лекция 2)

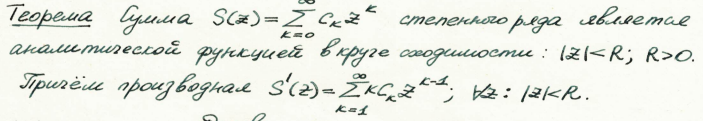
3. Геометрический смысл модуля и аргумента производной функции комплексной переменной. (лекция 3)

4. Определение конформного отображения в точке и в области. Теорема Римана о конформных отображениях (без док - ва).

Выяснить будет ли отображение конформным в области

5. Дробно - линейная функция. Круговое свойство. (лекция 3)

6. Интегральная теорема Коши для простого и сложного контура. (лекция 4)

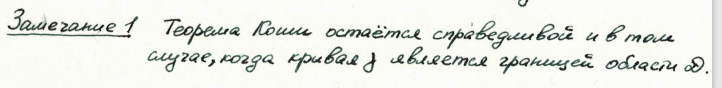
7. Интегральная формула Коши. (лекция 6)

8. Интеграл типа Коши. Существование производных любого порядка у аналитической функции. (лекция 6)

9. Неопределённый интеграл в комплексной области. Формула Ньютона - Лейбница. (лекция 6)

10. Теорема Морера. (лекция 6)

11. Ряд Тейлора. Единственность разложения в ряд Тейлора. (лекция 7)

12. Неравенства Коши для коэффициентов степенного ряда. Теорема Лиувилля. (лекция 7)

13. Теорема единственности аналитической функции. Изолированность её нулей. (лекция 7)

14. Теорема Лорана, ряд Лорана. Единственность разложения в ряд Лорана.

(лекция 8)

15. Устранимая особая точка аналитической функции. Поведение аналити- ческой функции в окрестности устранимой особой точки.(лекция 8)

16. Полюс аналитической функции. Поведение аналитической функции в окрестности полюса. (лекция 8)

17. Существенно особая точка аналитической функции. Поведение аналити- ческой функции в окрестности существенно особой точки. Теорема Сохоцкого - Вейерштрасса. (лекции 8 и 9)

18. Вычет аналитической функции относительно конечной и бесконечной изолированной особой точки. Вычисление вычета относительно полюса.

(лекции 9 и 10)

19. Основная теорема о вычетах. (лекция 10)

20. Теорема о сумме вычетов на расширенной комплексной плоскости. (лекция 10)

21. Вычисление несобственных интегралов 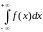с помощью вычетов.

(лекция 10)

22. Лемма Жордана.

­ (на следующей странице какое-то доказательство, вроде относится к лемме Жордана)

23. Вычисление интеграла 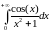с помощью леммы Жордана.

24. Преобразование Лапласа. Оригиналы и изображения. Показатель роста Полуплоскость сходимости. Аналитичность изображения ( без док - ва ). (лекция 11)

­­

25. Линейность преобразования Лапласа. Теоремы подобия, запаздывания и смещения. (лекция 11)

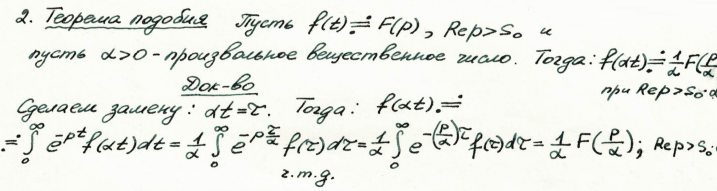
26. Теоремы о дифференцировании оригиналов и изображений. (лекции 11 и 12)

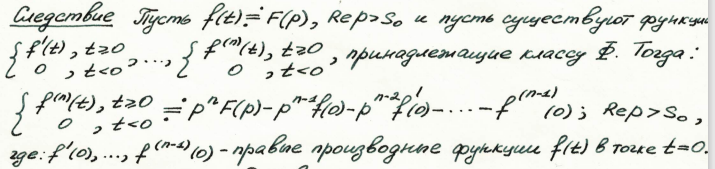
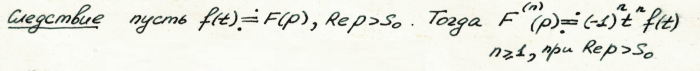
27. Теоремы об интегрировании оригиналов и изображений. (лекция 12)

28. Обращение преобразования Лапласа. Формула Меллина. (лекция 12)

­­

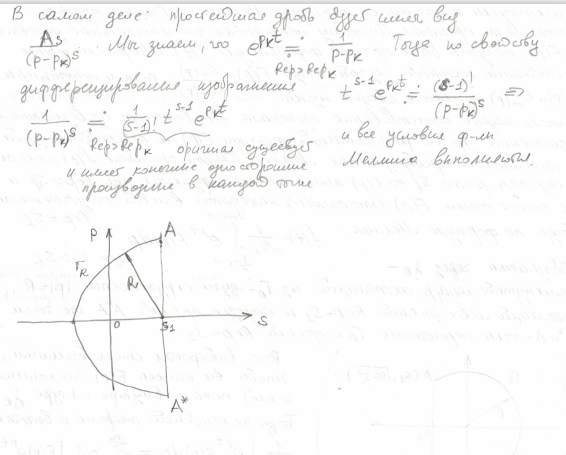
29. Первая и вторая теоремы разложения (для рациональной функции).