
Goryachev_Specialnye_glavy_funkcionalnogo_analiza_2013
.pdf1. Общие сведения |
21 |
пусть имеется произвольная числовая последовательность |
|
1 |
|
fungn1=1. Рассмотрим ряд n=1 an, у которого |
|
P |
|
a1 = u1; an = un un 1; n = 2; 3; : : : ; |
(1.10) |
и найд¼м его частичные суммы. Мы имеем, что
S1 = a1 = u1; S2 = a1 + a2 = u1 + (u2 u1) = u2; Sn = a1 + a2 + + an =
= u1 + (u2 u1) + + (un un 1) = un;
òî åñòü Sn = un при n = 1; 2; : : :. Следовательно, можно не только применять свойства последовательностей при изу- чении рядов (что уже делается), но и, наоборот, свойства рядов применять для изучения последовательностей.
При исследовании сходимости числовых последовательностей используется критерий Коши . Сформулируем его для рядов, имея в виду последовательность fSng частичных сумм числового ряда (1.2).
Т е о р е м а 1.3 (критерий Коши для рядов). Числовой
1
ðÿä P an сходится тогда и только тогда, когда для любого
n=1
" > 0 найд¼тся номер N, что для всех номеров n и m таких, что m > n > N, имеет место неравенство
m
X
ak < ":
k=n+1
Отметим, что в специальном доказательстве эта теорема не нуждается, так как она ранее была доказана для любых
числовых последовательностей в том числе и для последо-
1
вательности fSng частичных сумм ряда P an.
n=1
22 |
|
|
|
|
|
|
|
Часть I. Числовые ряды |
|
Т е о р е м а 1.4 (необходимый признак сходимости). Если |
|||||||||
|
1 |
|
|
|
|
|
|
|
|
|
nP |
|
|
|
|
|
|
|
|
числовой ряд |
an сходится, то |
|
|
||||||
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
lim an = 0: |
|
|||
|
|
|
|
n!1 |
|
|
|
||
= S. Но тогда и |
lim Sn |
|
1 |
= S, |
|
1 |
|
||
|
|
P |
|
||||||
Д о к а з а т е л ь с т в о. Пусть |
|
an = S, òî åñòü lim Sn = |
|||||||
|
|
|
|
|
|
|
|
n=1 |
n!1 |
|
n |
|
|
|
|
следовательно, |
|||
|
!1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
nlim an = nlim (Sn |
Sn 1) = nlim Sn nlim Sn 1 = S S = 0: |
||||||||
!1 |
!1 |
|
|
|
|
!1 |
|
!1 |
|
Теорема доказана.
Отметим, что эту теорему можно вывести из критерия Коши для рядов (из теоремы 1.3). Также отметим, что при решении примеров этот признак, являясь необходимым, используется для доказательства расходимости исследуемого ряда. Так, при исследовании сходимости рядов (1.4), мы видим, что при jqj > 1 (случаи 2 5) предел его общего чле-
íà lim an, òî åñòü |
lim qn либо вообще не существует, либо |
n!1 |
n!1 |
|
1 |
отличен от нуля, и поэтому ряд P qn в этих случаях расхо-
n=0
дится.
С другой стороны, установив, что lim an = 0, ìû íå
n!1
докажем сходимости ряда. П р и м е р. Рассмотрим ряд
1 |
|
1 |
|
1 |
|
1 |
1 |
|
|
||||
X |
|
|
= 1 + |
|
|
+ |
|
|
+ + |
|
+ ; |
(1.11) |
|
n |
2 |
3 |
n |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|

2. Знакоположительные ряды |
23 |
покажем, этот ряд расходится по теореме 1.3. Действительно, возьм¼м " = 12 > 0 и для любого номера N рассмот-
рим n = N + 1 и m = 2n (очевидно, что m > n > N). Но
|
m |
|
1 |
1 |
|
|
1 |
|
|
1 |
|
|
1 |
|
|||||
тогда k=n+1 ak |
|
|
|
|
> n |
|
= |
= ", |
|||||||||||
= n + 1 |
+ n + 2 + + |
2n |
2n |
2 |
|||||||||||||||
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n слагаемых |
|
|
|
|
|
|
|
|
|
||||
|
|
|
| |
|
|
|
{z |
|
|
|
} |
|
|
|
|
|
|
||
что и доказывает |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
расходимость ряда (1.11). |
|
|
|
|
|
|||||||||||
1.4.Вопросы для повторения и самостоятельной работы
1.Доказать теорему 1.1.
2.Составить числовой ряд, частичными суммами кото-
рого являются элементы последовательности
1; 12 ; 13 ; : : : ; n1 ; : : : :
Чему равна сумма полученного ряда?
3.Вывести необходимый признак сходимости (то есть теорему 1.4) из критерия Коши (из теоремы 1.3).
2.Знакоположительные числовые
ðÿäû
1
Числовой ряд P an называется знакоположительным ,
n=1
если для всякого n общий член an > 0.
24 |
Часть I. Числовые ряды |
Разумеется, согласно замечанию на с. 15 о том, что сходимость (расходимость) ряда не зависит от изменения конечного числа начальных слагаемых, достаточно считать, что неравенство an > 0 имеет место для всех n, начиная с
некоторого номера n0.
2.1.Критерий сходимости знакоположительных рядов
1 Т е о р е м а 2.1. Знакоположительный числовой ряд
P
an сходится тогда и только тогда, когда последователь-
n=1
ность fSng его частичных сумм ограничена сверху. При этом сумма ряда S = supfSng.
Äî ê à ç à ò å ë ü ñ ò â î. Частичная сумма Sn+1 = a1 +a2 +
++an+an+1 = Sn+an+1 > Sn, то есть последовательность fSng является возрастающей, а для таких последовательностей, как известно, критерием сходимости будет ограниченность сверху. При этом предел последовательности равен е¼ точной верхней грани. Теорема доказана.
Ясно, что если последовательность fSng не ограничена
сумма расходящегося |
|
|
|
|
1 |
|
|
|
|
|
|
P |
an = +1. В частности, |
||
сверху, то |
nlim Sn = +1, òî åñòü |
n=1 |
|||||
|
!1 |
|
|
|
|
|
|
|
|
гармонического ряда (1.11) |
|||||
|
|
1 |
1 |
|
|
|
|
|
|
X |
|
|
= +1: |
(2.1) |
|
|
|
n=1 |
|
n |
|||
|
|
|
|
|
|
|
|
Поэтому для знакоположительных рядов в качестве обозна- чения сходимости можно писать
1 |
|
X |
|
an < +1: |
(2.2) |
n=1
2. Знакоположительные ряды |
25 |
Äëÿ знакопеременных рядов, то есть для таких рядов, в которых как угодно далеко встречаются и положительные, и отрицательные слагаемые, обозначение (2.2) (ограниченность частичных сумм) уже не эквивалентно сходимости, что показывает пример расходящегося ряда (1.6) с ограни- ченными частичными суммами.
2.2.Признак сравнения. Интегральный признак
Òе о р е м а 2.2 (признак сравнения). Пусть существует такой номер n0, ÷òî
|
0 6 an 6 bn äëÿ âñåõ n > n0: |
(2.3) |
||
Тогда справедливы следующие утверждения. |
|
|||
|
1 |
1 |
|
|
1. Åñëè ðÿä |
P |
P |
|
|
|
bn сходится, то ряд |
an также сходится. |
||
|
n=1 |
n=1 |
1 |
|
дится. |
1 |
|
|
|
P |
|
nP |
|
|
2. Åñëè ðÿä |
|
an расходится, то ряд |
bn также расхо- |
|
|
n=1 |
|
=1 |
|
Ä î ê à ç à ò å ë ü ñ ò â î. Обозначим |
|
|
||
|
An = a1 + a2 + + an; |
|
||
|
Bn = b1 + b2 + + bn: |
(2.4) |
||
Так как (см. замечание на с. 15) отбрасывание конечного числа членов ряда не влияет на его сходимость (расходимость), то будем считать, что неравенство (2.3) справедливо для всех n 2 N. Но тогда из (2.4) вытекает, что
An 6 Bn: |
(2.5) |
26 |
Часть I. Числовые ряды |
1
Пусть ряд P bn сходится. Согласно теореме 2.1, последо-
n=1
вательность fBng ограничена сверху. Поэтому из (2.5) сле-
дует, что последовательность fAng также ограничена свер-
1
ху, то есть (опять по теореме 2.1) ряд P an сходится, что
n=1
доказывает первое утверждение.
1 |
|
1 |
Пусть теперь ряд |
an расходится. Если ряд |
bn ñõî- |
=1 |
1 |
n=1 |
nP |
P |
дится, то (как только что доказано) ряд P an также схо-
n=1
nlim |
an |
= k 2 (0; +1): |
(2.6) |
|
b |
n |
|||
!1 |
|
|
|
|
11
Тогда ряды P an è P bn сходятся или расходятся одновре-
n=1 n=1
менно.
Ä î ê à ç à ò å ë ü ñ ò â î. Согласно определению предела, для любого " > 0 найд¼тся номер n0, такой, что для всех
n > n0 |
|
абсолютная величина |
bn k |
< ", òî åñòü èìå- |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
an |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
an |
|
|
|||
ет место двойное неравенство |
k |
|
" < |
|
< k + ". Âîçü- |
|||||||||||||
bn |
||||||||||||||||||
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ì¼ì " = |
> 0. Тогда найд¼тся номер n0, такой, что |
|
||||||||||||||||
|
|
|
||||||||||||||||
2 |
|
|||||||||||||||||
|
|
|
|
k |
bn < an < |
3k |
bn |
äëÿ âñåõ n > n0; |
(2.7) |
|||||||||
|
|
|
2 |
2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
или, что то же самое, |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
2 |
an < bn < |
2 |
an |
äëÿ âñåõ n > n0: |
(2.8) |
|||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
3k |
|
k |
|
|
|
|
|
|
|
|||||
2. Знакоположительные ряды |
|
|
27 |
|||||
1 |
3k |
1 |
|
|
|
|
|
|
nP |
|
|
|
|
|
|||
Пусть ряд |
bn сходится. Тогда согласно теореме 1.1 |
|||||||
X |
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ðÿä |
|
bn также сходится и с использованием второго |
||||||
2 |
||||||||
n=1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
1 |
k |
||
|
|
|
|
nP |
||||
из неравенств (2.7), по теореме 2.2 ряд |
an является схо- |
|||||||
|
|
|
|
P |
=1 |
X |
|
|
дящимся. Если ряд |
|
|
|
|||||
bn расходится, то ряд |
|
|
bn также |
|||||
|
2 |
|||||||
|
|
|
|
n=1 |
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
(по теореме 1.1) расходится и, согласно первому из нера-
|
|
1 |
|
1 |
|
|
nP |
||
венств (2.7), по теореме 2.2 ряд |
an является расходя- |
|||
пользуя второе |
|
P |
|
=1 |
|
|
|
||
щимся. Если же ряд |
an сходится (расходится), то, ис- |
|||
|
|
n=1 |
|
|
|
(первое) из неравенств (2.8), теорему 1.1 и |
|||
ходится). Следствие доказано. |
1 |
|
||
nP |
|
|||
теорему 2.2, получаем, что ряд |
|
bn также сходится (рас- |
||
|
|
|
=1 |
|
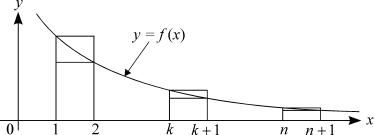
Т е о р е м а 2.3 (интегральный признак Коши Маклорена). Если при x > 1 функция f(x) > 0 и не возрастает,
òî
1 |
+1 |
|
|
Z |
|
|
|
n=1 f(n) è |
f(x) dx |
(2.9) |
|
X |
1 |
|
|
сходятся или расходятся одновременно.
Д о к а з а т е л ь с т в о. Обозначим через Sn частичные суммы ряда в (2.9). По условию
f(k) > f(x) > f(k + 1); x 2 [k; k + 1]; k = 1; 2; 3; : : : :
Интегрируя это двойное неравенство по переменной x от k
28 |
Часть I. Числовые ряды |
||
|
|
k+1 |
|
до k + 1 и используя очевидное равенство |
Rk |
dx = 1, имеем |
|
k+1 |
|
|
|
f(k) > Zk |
f(x) dx > f(k + 1); k = 1; 2; 3; : : : : |
||
Суммируя полученное двойное неравенство по k от 1 до n, получаем
n |
n |
k+1 |
n |
|
Z |
|
|||
k=1 f(k) > k=1 |
f(x) dx > k=1 f(k + 1); |
|||
X |
X k |
|
X |
|
òî åñòü |
|
n+1 |
|
|
|
|
|
||
Sn > Z1 |
f(x) dx > Sn+1 f(1): |
(2.10) |
||
1 |
|
|
|
|
Пусть ряд |
f(n) сходится. Согласно теореме 2.1, после- |
|||
=1 |
|
|
|
|
довательностьnP |
|
ограничена сверху. Поэтому по первому |
||
fSng |
|
|
|
|
из неравенств (2.10) следует, что числовая последователь-
ность также ограничена сверху. Но по усло-
вию f(x) > 0, следовательно, неубывающая функция F (T )=

2. Знакоположительные ряды |
29 |
T
R
=f(x) dx является ограниченной сверху, и поэтому суще-
1 |
|
+1 |
|
|
|
|
T !+1 |
1 |
( |
|
) |
|
|
R1 |
x |
dx |
||||
ствует lim |
F (T ), то есть несобственный интеграл f |
|
|
|||
|
nP |
|
|
|
|
|
сходится. Åñëè ðÿä |
f(n) расходится, то, согласно теоре- |
|||||
|
=1 |
|
|
|
|
|
ме 2.1, последовательность fSng, а значит, и последовательности fSn+1g è fSn+1 f(1)g не ограничены сверху. Поэтому по второму из неравенств (2.10) следует, что последо-
|
|
+1 |
|
|
|
вательность |
n1 |
f(x) dx также не ограничена сверху, то |
|||
åñòü |
|
R |
|
+1 |
|
|
+1 |
|
R1 |
|
|
|
несобственный интеграл |
f(x) dx расходится. Если |
|||
çóÿ |
|
R |
|
|
|
же интеграл |
|
f(x) dx сходится (расходится), то, исполь- |
|||
|
|
1 |
|
|
|
|
неравенство (2.10), неотрицательность и монотонность |
||||
|
|
|
|
|
1 |
функции f(x) и теорему 2.1, получаем, что и ряд |
nP |
||||
f(n) |
|||||
|
|
|
|
|
=1 |
сходится (расходится). Теорема доказана.
Проиллюстрируем только что доказанный интегральный признак следующими п р и м е р а м и.
П р и м е р 1. Рассмотрим ряд
1 |
1 |
1 |
1 |
1 |
|
|
|||
X |
|
= 1 + |
|
+ |
|
+ + |
|
+ |
(2.11) |
n=1 |
np |
2p |
3p |
np |
|||||
|
|
|
|
|
|
|
|
|
|
1
то есть ряд с общим членом an = np при различных значе- ниях p. В частности, при p = 1 получается введ¼нный ранее
гармонический ряд (1.11). Рассмотрим два случая.
1. Пусть p 6 0. Тогда lim an 6= 0(этот предел равен
n!1

30 |
Часть I. Числовые ряды |
либо 1 при p = 0, либо +1 при p < 0), поэтому ряд (2.11) расходится по необходимому признаку (см. теорему 1.4).
1
2. Пусть p > 0. Функция f(x) = xp ïðè ýòèõ p (даже при p > 0) удовлетворяет условиям теоремы 2.3, а инте-
ãðàë |
+1 |
xp , как известно, сходится при p > 1 и расходится |
Z1 |
||
|
|
dx |
при p 6 1. Следовательно в этом случае ряд (2.11) сходится при p > 1 и расходится при 0 < p 6 1.
Объединяя эти два случая, получаем, что ряд |
|
|||||||||||||
|
1 |
|
1 |
|
ïðè p > 1 |
сходится, |
|
|||||||
|
|
X |
|
|
ïðè p 6 1 |
|
|
|
|
|
(2.12) |
|||
|
|
n=1 |
np |
|
расходится. |
|||||||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
П р и м е р 2. Рассмотрим ряд |
|
|
|
|
|
|
||||||||
1 |
1 |
|
|
1 |
1 |
|
1 |
|
|
|
||||
X |
|
= |
|
|
|
+ |
|
+ + |
|
|
+ ; (2.13) |
|||
n=2 |
n lnp n |
2 lnp 2 |
3 lnp 3 |
n lnp n |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
при различных |
||||
то есть ряд с общим членом an |
= |
|
||||||||||||
n lnp n |
||||||||||||||
значениях p. Здесь, в отличие от предыдущего примера, для всех p 2 (1; +1) общий член стремится к нулю (при p > 0 это совершенно очевидно, а при p < 0 в этом легко убедить-
ся, вычисляя предел lim |
ln p z |
, представляющий из себя |
|
z |
|||
z!+1 |
|
неопредел¼нность вида |
1 |
, по правилу Лопиталя). Рассмот- |
||||||||
рим те же самые два случая,1 |
что и в предыдущем примере. |
|||||||||
|
|
|
1 |
|
|
1 1 |
|
|
||
1. Пусть p 6 0. Тогда an > |
|
|
(ïðè n > 3), à ðÿä |
|
|
|
|
|||
|
|
n |
||||||||
|
|
|
n |
|
|
|
||||
X
n=2
расходящийся гармонический ряд (1.11) без первого слагае-
