Goryachev_Specialnye_glavy_funkcionalnogo_analiza_2013

182 Часть III. Ряды Фурье

последовательность не являет-

ся сходящейся в этом пространстве, так как е¼ предел не принадлежит Q0[ 1; 1] (у функции f(x) бесконечно много

точек разрыва). Итак, пространство Q0[ 1; 1] (то есть и пространство Q0[a; b]) не является полным. Аналогично устанавливается и неполнота пространств Q0Lp[a; b], если заметить, что подобно тому, как в предыдущем пункте из равномерной сходимости была выведена сходимость в смысле Lp, так и из равномерной фундаментальности можно вывести

фундаментальность в смысле Lp, то есть в нашем примере фундаментальность последовательности fn(x) 1n=1 â ïðî-

Q0Lp[ 1; 1] (à

значит, и пространство Q0Lp[a; b]) также не является полным.

Пространства CLp[a; b] и пространства C Lp[a; b].

Так же, как и в предыдущем примере, положим [a; b]

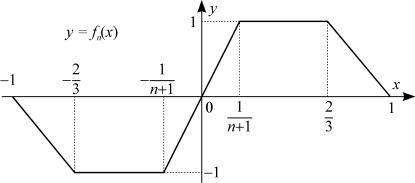
[ 1; 1] и рассмотрим на этом отрезке функциональную последовательность fn(x) 1n=1:

>

>

>

:

Легко видеть, что последовательность fn(x) 1n=1 ñõî- дится в каждой точке отрезка [ 1; 1], точнее,

lim fn(x) = f(x) äëÿ âñåõ x 2 [ 1; 1];

n!1

ãäå

димость в смысле Lp. Отметим попутно, что равномерной сходимости здесь и не может быть, так как предельная функ-

ция f(x) разрывна. Установим непосредственно фундамен-

тальность последовательности fn(x) 1n=1 в пространствах CLp[ 1; 1] è C Lp[ 1; 1] (легко видеть, что для любого n

функция fn(x) принадлежит обоим этим пространствам) и е¼ сходимость в смысле Lp к функции f(x). Действительно, пусть для определ¼нности m > n. Тогда пара функций fn(x)

184 Часть III. Ряды Фурье

è fm(x), как и пара функций fn(x) и f(x), отличаются друг

ч¼м абсолютная величина разности функций внутри каж-

дой пары всегда меньше единицы. Поэтому как величина

1

R

kfn fmkpp = jfn(x) fm(x)jp dx, так и величина kfn fkpp =

1

1

R

= jfn(x) f(x)jp dx оцениваются сверху значением инте-

1

1

Первое из неравенств в (7.41) говорит о том, что последовательность fn(x) 1n=1 является фундаментальной в про- странствах CLp[ 1; 1] è C Lp[ 1; 1], а второе из неравенств в (7.41) о том, что последовательность fn(x) 1n=1 сходит-

ся в смысле Lp к функции f(x), которая, как уже отме-

чалось, разрывна и поэтому не принадлежит ни пространству CLp[ 1; 1], ни пространству C Lp[ 1; 1]. Следователь-

но, пространства CLp[ 1; 1] è C Lp[ 1; 1] (а вместе с ними и пространства CLp[a; b] è C Lp[a; b]) не являются полными.

7.7. Вопросы для повторения

èсамостоятельной работы

1.Установить единственность нулевого элемента линейного пространства.

2.Установить, что для всякого элемента x из линейного пространства L противоположный элемент единствен.

двух элементов x 2 E и y 2 E определено вещественное число (x; y), называемое скалярным произведением элемента x

на элемент y и удовлетворяющее следующим свойствам.

1. Для любых x 2 E, y 2 E справедливо равенство

2.Для любых x 2 E, y 2 E и любого вещественного числасправедливо равенство

3. Для любых x 2 E, y 2 E, z 2 E справедливо равенство

4.Для всякого x 2 E скалярное произведение (x; x) > 0, прич¼м (x; x) = 0 тогда и только тогда, когда x = .

Напомним, что нулевой элемент пространства E.

Эти четыре свойства называются основными свойствами или, как иногда говорят, аксиомами вещественного евклидова пространства. Из них сразу вытекает, например, следующее свойство. Пусть x и y произвольные элемен-

ты пространства E, а любое вещественное число. Тогда (x; y) = (по первому свойству) = ( y; x) = (по второму свойству) = (y; x) = (по первому свойству) = (x; y), то есть для любых x 2 E, y 2 E и любого вещественного числасправедливо равенство

В дальнейшем будем, если специально не оговорено, рассматривать комплексное евклидово пространство, а аналогичные результаты для вещественного евклидова пространства будем давать в виде задач для самостоятельной работы. При этом будем стараться употреблять формулировки, которые годились бы как для вещественного, так и комплексного случая.

Т е о р е м а 8.1 (неравенство Коши Буняковского). Для любых элементов x, y произвольного евклидова простран-

ства E справедливо неравенство1

В этом случае оба элемента x 6= , y 6= , и, следовательно,

По свойствам скалярного произведения для любого (комплексного) числа имеем

0 6 (x + y; x + y) =

1Разумеется, для вещественного евклидова пространства неравенство (8.7) можно записать в виде

(x; y)2 6 (x; x)(y; y):

Однако оно записано со знаком модуля, чтобы формулировка неравенства Коши Буняковского была верной как для вещественного òàê è

комплексного случая.

Из (8.8) также вытекает, что комплексное число (x; y) можно представить в виде

Подставим в соотношение (8.10)

= t ei ; t 2 ( 1; +1)

èрассмотрим скалярное произведение (x + y; x + y) как функцию вещественного переменного t:

'(t) = (x + t ei y; x + t ei y); t 2 ( 1; +1):

Из (8.8) (8.11) вытекает, что квадратный тр¼хчлен

'(t)=(y; y) t2 +2 j(x; y)j t+(x; x) > 0 äëÿ âñåõ t2( 1; +1):

Это означает, что его дискриминант (2B)2 4AC неотрицателен, следовательно,

4 = B2 AC = j(x; y)j2 (x; x)(y; y) > 0:

Поэтому неравенство (8.7) и в этом случае выполняется. Теорема доказана.

Евклидово пространство E становится линейным норми-

рованным пространством, если ввести в н¼м норму по фор-

ìóëå

p

kxk (x; x) : (8.12)

Проверим, что формула (8.12) зада¼т норму. Действительно, из четв¼ртой аксиомы скалярного произведения вытекает, что норма kxk определена для всех x 2 E, она неот-

рицательна и обращается в нуль тогда и только тогда, когда