Goryachev_Specialnye_glavy_funkcionalnogo_analiza_2013

Отсюда, в частности, следует, что для любого натурального n для всякого " > 0 найд¼тся номер N, что для любых

номеров i > N, j > N имеет место неравенство

то есть для любого натурального n числовая последователь-

n=1

Докажем, что a~ 2 l1 è a~ = lim a(i). Переходя к пределу при

i!1

j ! 1 в неравенстве (7.34) получаем, что для всякого " > 0 найд¼тся номер N, что для любого номера i > N имеет место неравенство

1

ka(i) a~k1 = Xja(ni) a~nj 6 2" :

Если установить, что множества lp (p > 1), о которых упоминается на с. 161, линейные нормированные пространства, то можно доказать, что эти пространства также являются полными.

Т е о р е м а 7.7. Пространство C[a; b] непрерывных на отрезке [a; b] функций полное пространство.

д¼тся номер N, что для любых номеров n > N, m > N и любого x 2 [a; b] имеет место неравенство

Коши равномерной сходимости функциональной последовательности). Поэтому она равномерно сходится на отрезке [a; b] к функ-

ции f(x), которая в силу теоремы 5.12 непрерывна на отрез-

êå [a; b]. Èòàê,

[a;b]

fn(x) f(x) 2 C[a; b]:

Переходя в (7.35) к пределу при m ! 1 и пользуясь непрерывностью нормы (третье утверждение теоремы 7.3), полу-

174 Часть III. Ряды Фурье

чаем: для всякого " > 0 найд¼тся номер N такой, что для любого номера n > N имеет место неравенство

доказана.

С л е д с т в и е. Пространство C [a; b] полное пространство.

Ä î ê à ç à ò å ë ü ñ ò â î. Линейное нормированное пространство C [a; b] является подпространством банахова ïðî-

странства C[a; b], следовательно, по только что доказанной

теореме 7.7 любая фундаментальная последовательностьfn(x) 1n=1 â C [a; b] сходится (прич¼м равномерно) к неко-

торой функции f(x) 2 C[a; b]. Равенство f(b) = f(a) сохраняется при предельном переходе. Поэтому f(x) 2 C [a; b]. Следствие доказано.

7.5. Сравнение различных видов сходимости

Остальные рассмотренные нами примеры линейных нормированных пространств, как мы увидим ниже (см. п. 7.6), являются примерами неполных пространств. Но прежде чем начать их рассматривать, то есть указывать фундаментальные последовательности, не сходящиеся в этих пространствах, сравним между собой различные виды сходимости функциональных последовательностей на отрезке [a; b].

Итак, пусть имеется сходящаяся на [a; b] функциональ-

Эта сходимость есть не что иное, как сходимость по нор-

ме пространств C[a; b], C [a; b] или Q0[a; b]. Действительно, пусть fn(x) 1n=1 сходящаяся последовательность или в C[a; b], èëè â C [a; b], èëè â Q0[a; b] к функции f(x) из соот-

ветствующего пространства, то есть

Тогда из определения нормы в этих пространствах (7.9), (7.10), (7.11) и понятия сходимости вытекает, что если для всякого " > 0 найд¼тся номер N, что для любого номера

n > N имеет место одно из неравенств

Таким образом, для всякого " > 0 найд¼тся номер N, что для любого номера n > N и для всех x 2 [a; b] абсолютная

величина jfn(x) f(x)j < ". А это как раз и означает, что последовательность fn(x) 1n=1 равномерно на [a; b] сходится к

функции f(x).

2. Поточечная сходимость, о которой упоминается на с. 87 (см. (5.3) и (5.4)):

Отметим, что в отличие от равномерной сходимости (7.36), которую, как мы сейчас видели, можно трактовать как сходимость по норме некоторых линейных нормированных пространств, поточечная сходимость (7.37) не является сходимостью по норме какого бы то ни было линейного нормированного пространства. Поскольку этот факт мы использовать не будем, то и не станем его обосновывать.

176 Часть III. Ряды Фурье

3. Сходимость в смысле Lp (p > 0). Функция f(x) на-

зывается пределом в смысле Lp функциональной последо- вательности fn(x) 1n=1 на отрезке [a; b], åñëè

Такая сходимость, естественно, является сходимостью по норме пространств CLp[a; b], C Lp[a; b] èëè Q0Lp[a; b]. Ýòè

пространства упомянуты на с. 161, где также сказано, что в следующем разделе будут введены пространства CL2[a; b], C L2[a;b] è Q0L2[a;b] (см. пространства (8.14) с нормой (8.17)).

Таким образом, можно по крайней мере считать, что число p

равняется 1 или 2. Если же вс¼-таки установить (хотя это и не очень просто), что формула (7.15) зада¼т норму в этих пространствах при всех p > 1, а не только при p = 1 или

p = 2, то последующие выкладки этого пункта справедливы и для указанных p.

Выясним, как связаны между собой эти виды сходимости. Мы уже знаем, что из равномерной сходимости вытекает поточечная (п. 5.2, с. 88). Установим, что из равномерной сходимости вытекает сходимость в смысле Lp. Действитель- но, пусть функциональная последовательность fn(x) 1n=1

равномерно сходится к функции f(x) на [a; b], то есть для любого " > 0 найд¼тся номер N, что для всех номеров n > N и для всех x 2 [a; b] абсолютная величина jfn(x) f(x)j <

ство (7.38), из которого следует, что функциональная последовательность fn(x) 1n=1 сходится в смысле Lp к функции

f(x) íà [a; b].

Иных связей между равномерной сходимостью (7.36), поточечной сходимостью (7.37) и сходимостью (7.38) в смыс- ëå Lp не имеется, в ч¼м мы сейчас убедимся, рассмотрев примеры функциональных последовательностей, сходящихся поточечно, но не являющихся сходящимися равномерно и в смысле Lp; а также функциональных последовательно- стей, сходящихся в смысле Lp, но не являющихся сходящимися ни равномерно, ни поточечно.

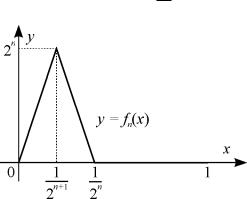
Рассмотрим на отрезке [a; b] [0; 1] функциональную по-

>

>

>

>

>

:

куда вытекает отсутствие фундаментальности, а значит, и

сходимости в смысле Lp функциональной последовательно- ñòè fn(x) 1n=1.

Чтобы убедиться в том, что из сходимости в смысле Lp не вытекает, вообще говоря, ни равномерной, ни даже поточечной сходимости, рассмотрим на отрезке [a; b] [ 1; 1] функциональную последовательность fn(x) 1n=1:

рассматриваемой последовательности на [ 1; 1] нет ни по-

точечной, ни тем более равномерной сходимости. Однако эта последовательность сходится в смысле Lp

1

7.6.Примеры неполных линейных нормированных пространств

Помимо введ¼нных на с. 157 160 линейных нормированных пространств Q0[a; b], CL1[a; b], C L1[a; b] è Q0L1[a; b] òàê-

же рассмотрим (и установим неполноту) линейных норми-

180 Часть III. Ряды Фурье

рованных пространств CLp[a; b], C Lp[a; b] è Q0Lp[a; b] (äëÿ âñåõ p > 1 èëè õîòÿ áû ïðè p = 2).

Мы укажем фундаментальные последовательности, не являющиеся сходящимися в этих пространствах.

Пространство Q0[a; b] и пространства Q0Lp[a; b].

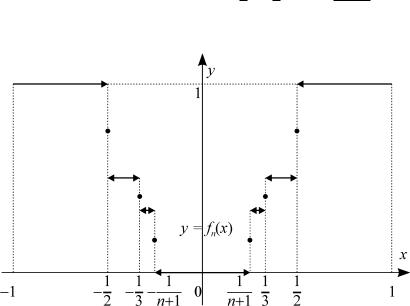
Рассмотрим на отрезке [a; b] [ 1; 1] функциональную последовательность fn(x) 1n=1:

>

>

>

>

>

: