Поверхностный интеграл 2 рода
Нахимовский проспект 45
Москва, Комсомольский проспект, 21/10, кинотеатр "Горизонт"
Поверхностный интеграл 2 рода
Скамейка в Киеве |
Лента Мебиуса в Екатеринбурге |
Лондон. Гагарин, стоящий |
|
на ленте Мебиуса. |
Музей истории и техники в Вашингтоне |
|
Поверхностный интеграл 2 рода
В рассказе «Лист Мебиуса» автора А. Дж. Дейча, бостонское метро строит новую линию, маршрут которой становится настолько запутанным, что превращается в ленту Мёбиуса, после чего на этой линии начинают исчезать поезда (http://lib.ru/RAZNOE/subway.txt)
По мотивам рассказа было снято несколько фильмов: 1988 (СССР, режиссер Леонид Партигул) “Лист Мебиуса”, 1993 (Германия, режиссер Матти Гешоннек) “Мебиус”, 1996 (Аргентина, режиссер Густаво Москера) “Мебиус”, 2005 (Германия, режиссер Джо Пройслер) “Мебиус 17”.
фильм Партигула: http://www.youtube.com/watch?v=AuJockV3KVg http://www.youtube.com/watch?v=m5iYfaZ3BU0
фильм Гешоннека: http://kinofilms.tv/film/myobius/53931/
фильм Москера: http://1kinotv.ru/prikliuchenia/9632-mebius-1996.html фильм Пройслера: http://kinozon.tv/65163
Поверхностный интеграл 2 рода
Существуют технические применения ленты Мёбиуса. Полоса ленточного конвейера выполняется в виде ленты Мёбиуса, что позволяет ему работать дольше, потому что вся поверхность ленты изнашивается равномерно. Также в системах записи на непрерывную плёнку применяются ленты Мёбиуса (чтобы удвоить время записи). Во многих матричных принтерах красящая лента также имеет вид листа Мёбиуса для увеличения её ресурса.
Устройство под названием резистор Мебиуса — это недавно изобретенный электронный элемент, который не имеет собственной индуктивности.
Есть гипотеза, что спираль ДНК сама по себе тоже является фрагментом ленты Мебиуса и только поэтому генетический код так сложен для расшифровки и восприятия. Больше того – такая структура вполне логично объясняет причину наступления биологической смерти – спираль замыкается сама на себя и происходит самоуничтожение.
Поверхностный интеграл 2 рода
n a
(поле нормалей)
(заданное векторное поле)
a {P,Q, R}
S
Определение.
Нормальная компонента векторного поля – это проекция векторного поля на поле нормалей an (a, n)
| n |
adS Pdydz Qdzdx Rdxdy andS
S S S
Поверхностный интеграл 2 рода
a {P,Q, R}
Пусть , ,
углы, которые образует нормаль с осями координат, тогда
an P cos Q cos R cos .
Поэтому
S
adS (P cos Q cos R cos )dS
S S
Поверхностный интеграл 2 рода
|
|
|
|
|
(1) ( a |
b)dS adS bdS |
|||
S |
|
|
S |
S |
|
|
(S-1 – это та же поверхность S, но |
||
(2) adS |
adS |
|
||
|
ориентированная противоположно) |
|||
S 1 |
S |
|
|
|
(3)Для любого разбиения |
U {S1, S2 ,..., Sn}, |
|||
|
|
n |
|
|
|
adS adS |
|
||
|
S |
i 1 |
Si |
|
(4)Если векторное поле перпендикулярно нормали, то
adS 0
S
Поверхностный интеграл 2 рода
(5) Любое векторное поле можно представить следующим образом
a {P,Q, R} {P,0,0} {0,Q,0} {0,0, R}
поэтому
adS Pdydz Qdzdx Rdxdy
S S
Pdydz Qdzdx Rdxdy
S S S
|
Поверхностный интеграл 2 рода |
|
Формулы для вычисления |
|
|
v |
x x(u, v) |
|
|
|
|
Ω |
|
|
|
|
|
u |
y y(u, v) |
S |
|
||
|
z z(u, v) |
|
(u, v)
|
x |
, |
y |
, |
|
z |
||
ru |
|
u |
u |
|
|
|
||
|
|
|||||||
|
|
|
|
|
u |
|||
|
x |
, |
y |
, |
z |
|||
rv |
|
v |
v |
|
|
|||
|
|
|
|
v |
||||
an |
(a, r r ) |
a {P(x(u, v), y(u, v), z(u, v)), |
||
|
u v |
Q(x(u, v), y(u, v), z(u, v)), |
||
|
|
| r |
r | |
|
dS | |
u |
v |
R(x(u, v), y(u, v), z(u, v))} |
|
ru rv | dudv |
||||
|
|
|
|
|
|
|
|
(ориентация |
S |
adS |
|
andS |
|
(a, ru |
rv )dudv |
||||
|
|
|
|
|
|
|
согласована |
с |
|
|
|
|
|
|
положительной |
||||
S |
|
S |
|
|
|
|
ориентацией |
|
|
|
|
|
|
|
|
|
|
плоскости (u,v)) |
|
|
|
|
|
|
|
|
|
||
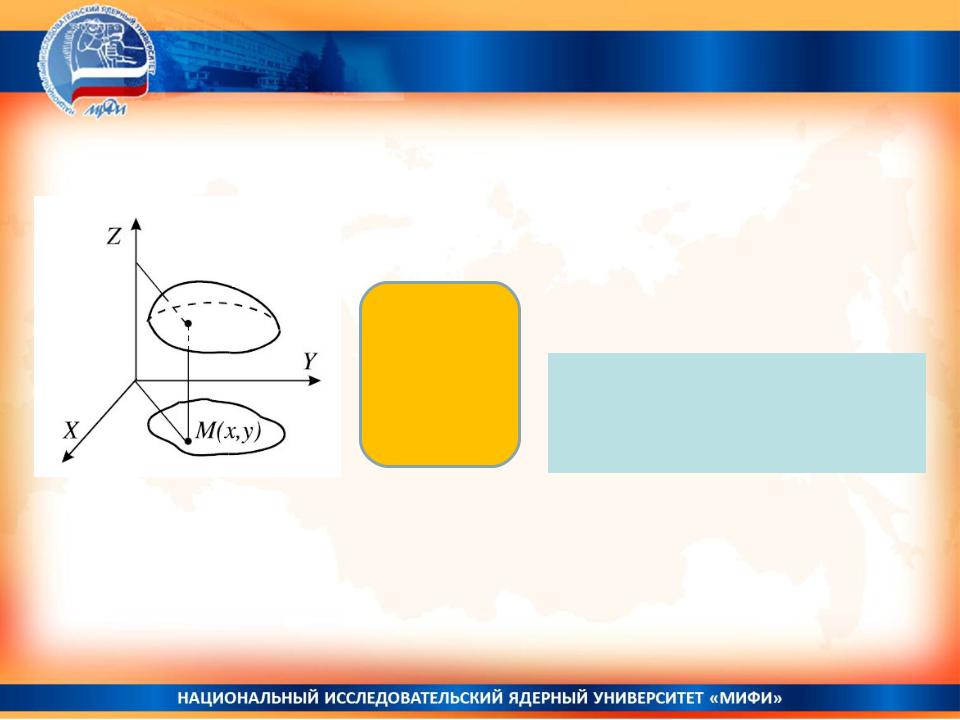
Поверхностный интеграл 2 рода
Случай поверхности, заданной как график явной функции z=φ(x,y), и векторного поля параллельного оси Oz
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a {0,0, R} |
|
|
adS Rdxdy |
||||||||
|
z (x, y) |
|
|
|
|
|
|
|
S |
|
S |
|
|
|
|
|
|
|
|
|
|
u |
|
1,0, / |
, |
||||
|
|
|
|
|
|
|
|
|
r |
|
x |
|||
|
S |
|
x u |
|
|
|
|
|
0,1, / y |
, |
||||
|
|
|
|
|
|
r |
||||||||
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
y v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
z (u, v) |
|
|
r r |
{ / x, / y,1} |
|||||||
|
|
|
|
|
|
|
|
u |
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
{ / x, / y, 1} |
|||
|
|
|
(u, v) |
|
|
rv |
ru |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для согласованных ориентаций: |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(a, ru rv ) R |
|
|
rv )dudv |
|
|
|||||||||
|
adS |
(a, ru |
R(x, y, (x, y))dxdy |
|||||||||||
S |
|
|