Добавил:

okley Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский ядерный университет (МИФИ)

Предмет:

Векторный и тензорный анализ

Файл:

Лекции / VTA_lektsia_5

.pdf

Скачиваний:

Добавлен:

17.05.2024

Размер:

450.44 Кб

Скачать

☆

Ф-03- лекция 5. Тройной интеграл. П.1 Измеримые множества в пространстве.

«Кирпичиком» для построения измеримых множеств в пространстве R										3	является
											является
параллелепипед Пabc x, y, z : xi x xi			a, y j				y y j b, zk z zk c с вершиной в
точке xi , y j , zk , его параметр d (Пabc )			a	2	b	2	c	2	- диагональ параллелепипеда.
точке xi , y j , zk , его параметр d (Пabc )			a		b		c		- диагональ параллелепипеда.
ОПР. Телом G в пространстве называют открытую, односвязную и ограниченную область
в R	3	. Замкнутая область – это G G G , где G - совокупность граничных точек.
в R
ОПР. Ступенчатым телом G называют объединение параллелепипедов П , возможно
пересекающихся по границе, G = П . Ступенчатое тело G вписано в G , если

П		G, , и описано, если G G	. Параметром d (G ) ступенчатого тела называют
число d (G ) = max d (П ) .

ОПР. Нижней мерой тела G называется число (G) sup (G ) , где верхняя грань берется

по всем ступенчатым телам, вписанным в G . Верхняя мера тела G называется число
					G - ступенчатые тела, описанные около G . Числа (G) и	(G)
	(G) inf (G ) , где


существуют для любого G .
ОПР. Тело G				измеримо в пространстве, если (G) = (G) = (G) .
Число			(G) называется мерой тела G или его объемом.
ПРИМЕРЫ измеримых областей.
1. Пabc			(x, y, z) R3		: x0 x x0 a, y0 y y0 b, z0 z z0 c - параллелепипед со
сторонами a,b, c и вершиной (x0 , y0 , z0 ) , Пabc abc
2. TD			D a;b x, y, z : x, y D, z a;b - прямой цилиндр, образующая которого
		a,b

перпендикулярна плоскости ХОУ, с основанием D и высотой b a , где (D) - площадь

области D .
ПОЯСНЕНИЕ. Если D П		ступенчатая область, вписанная в D , то объединение

				a,b
параллелепипедов П a;b является ступенчатым телом, вписанным в TD
Его объем при d (D ) 0	стремится к величине (T		a,b	) (b a) (D) .
Его объем при d (D ) 0	стремится к величине (T			) (b a) (D) .
		D

3. VDf ,g x, y, z : x, y D, g(x, y) z f (x, y) - стандартная область по оси ОZ,

где

g(x, y), f (x, y) кусочно-гладкие функции в измеримой области D

на плоскости R2 .

(VDf ,g )		f (x, y g(x, y))dxdy .
(VDf ,g )		f (x, y g(x, y))dxdy .
	D
ПОЯСНЕНИЕ. Если D П ступенчатая область, вписанная в D и

			m ( f ) min f (M ) , M ( f ) max f (M ) .
				M П	M П

Тогда объединение параллелепипедов П M (g);m ( f ) представляет ступенчатое тело,
		f ,g		, а объединение параллелепипедов П m (g);M ( f ) - ступенчатое
вписанное вVD
тело, описанное околоV f ,g . Предел объемов каждого из них при d (D ) 0						равен
				D
				(VDf ,g ) f (x, y g(x, y))dxdy .
					D
4. Тело Gc с измеримыми сечениями.					Рассматриваются тела G , у которых сечения

плоскостями перпендикулярными координатным осям, например, плоскостями с уравнением z p , измеримы на плоскости ХОУ, т.е. для любого p a,b область

D		x, y	R	2	: x, y, p
				2
	p
переменной			p на отрезке

a;b

измерима и ее

. Множество G

мера

p	x,

y, z :

непрерывная функцияx, y Dp , z p назовем

сечением тела G плоскостью z p . Тогда тело

и (G )

)dp ее объем.

p a,b

ПОЯСНЕНИЕ. Если a 0 , 1,..., k , k 1,... n

разбиение отрезка

a;b

с параметром

разбиения d . Разбиение пересечения D

на прямоугольники D

= П

k 1

порождает разбиение тела G на параллелепипеды

П k ; k 1 . Объем ступенчатого тела,

		n	) ) k 1 k , где o(1)
построенного из них равен ( (D			) ) k 1 k , где o(1)	при
			k
		л 0
	b
стремится к (G)		(Dp )dp при уменьшении параметра разбиения.
стремится к (G)		(Dp )dp при уменьшении параметра разбиения.
	a

d (D )

В частности, цилиндр 2) тело с измеримыми сечениями и (Dp ) (D)																															-	постоянная на
отрезке a,b функция.
ПРИМЕР 1. Найти объем тела ограниченного поверхностями:
										z x y ,				z xy , x y 1,							x 0		,	y 0 .
РЕШЕНИЕ. Рассмотрим сечения плоскостями y p 0;1 .Тогда область																																Dp (трапеция) на
плоскости					XOZ			имеет границы						z x p ,				z px , x 1 p ,							x 0			и ее мера (площадь)
				1 p								x p				px	2			1
				1 p								x p				px				1
														2							1 p(1 p)							- непрерывная функция
(Dp )					x p px dx													1 p							2	p	2
																		1 p							2		2
													2			2		0		2
				0									2			2				2
				0																		1	1	1 p(1 p)							dp
																							1
на отрезке [0;1]. Тогда объем тела															G	равен:			(G)									2	p	2
																												2		2
																						2
																						2	0
																							0
	1	1										7
	1											7
			1 p		p	2	p		3	dp .
						2			3
	2	0									24
		0
П.2 Тройной интеграл.
Пусть G - измеримое тело и													G = П соответствующее разбиение G на

параллелепипеды. В каждом параллелепипеде																				П выберем произвольную точку P П .
ОПР. Интегральной суммой функции f (x, y, z)																				по области G						называют выражение:
												S f (G ) f (P ) (П ) .

ОПР. Тройным интегралом Римана функции

f (x, y, z)

по области

называют число:

f (x, y, z)dxdydz

lim d ( ) 0

S	f

)

Если функция имеет тройной интеграл, то она называется интегрируемой по Риману в области G .

ТЕОРЕМА 1. (необходимое условие интегрируемости)

Если функция f (x, y, z) интегрируема в измеримой области G , то она ограничена в G .

ДОК. (аналогично соответствующей теореме для двойного интеграла) ТЕОРЕМА 2. (достаточное условие интегрируемости)

Всякая кусочно-непрерывная на измеримом множестве G функция интегрируема по Риману.

ДОК. (аналогично соответствующей теореме для двойного интеграла)

СВОЙСТВА ТРОЙНОГО ИНТЕГРАЛА. (аналогичны свойствам двойного интеграла).

1. линейность:		f g)dxdydz		fdxdydz		gdxdydz
1. линейность:		f g)dxdydz		fdxdydz		gdxdydz
	G		G		G

2. аддитивность по множеству G G1 G2 , где

пересекающиеся по границе. Тогда		fdxdydz

G1 и G2 - измеримые множества,

		fdxdydz		fdxdydz .

G	G	G
	1	2

теорема о среднем. Если c , yc , zc G , для которой

f (x, y, z) непрерывна на G

	f (x
f (x, y, z)dxdydz	f (x	,
	c
G

, то существует точка

yc , zc ) (G) .

4. Оценка отклонения интеграла от интегральной суммы:

f (x, y, z)dxdydz S f (G ) f ( ) (G) ,

где G - любое разбиение G на параллелепипеды с параметром

колебания f (x, y, z) : f	( )	sup		f (M1 ) f (M	2 )
		( M	,M	)
		1	2

, а

	f

( )

- функция

Для непрерывной функции f (x, y, z)

на

колебание

	f

( )

бесконечно малая функция в

точке

5. Если

(

x, y, z) =

1, x, y, z G
	x, y, z G
0,

- характеристическая функция области

, то

(G)

(x, G

z)dxdydz

П.3 Повторные интегралы.

Вычисление тройного интеграла сводится к вычислению двойных и одномерных интегралов, т.е. к повторному интегрированию. Для областей, рассмотренных выше, эта процедура следующая (рассматриваются функции F(x, y, z) кусочно-непрерывные в G ).

1. Для G = Пabc :

F (x, y, z)dxdydz

x	a		y	b		z	c
0			0			0
		dx			dy	F (x, y, z)dz

(1)

G	x	y	0	z	0
	0
Внутренний одномерный интеграл берется по переменной z на отрезке z0 ; z0 c , при
фиксированных (x, y) и поэтому является непрерывной функцией двух переменных x, y .

Интегрирование этой функции по переменной y на отрезке y0 ; y0 b при фиксированном

x задает функцию переменной x , которая интегрируется на отрезке x0 ; x0 a

Док.

x a

y b

z c

x a

y b

x a

y j 1

dy F (x, y, z)dz

dx F (x, y, zk )dy

k 1

j 1 y

n,m

p xi 1

n,m, p

zk y j F (x, y j , zk )dx

F (xi , y j , zk ) xi y j zk

k , j 1

i 1 xi

k , j ,i 1

для некоторых точек xi , y j

, zk , xi xi ; xi 1 , y j y j ; y j 1 , zk zk ; zk 1 . Последнее

представляет интегральную сумму тройного интеграла и ее предел равен с одной стороны тройному интегралу, а с другой повторному.

Порядок интегрирования по прямоугольнику может быть изменен.

Пример 2. Вычислить интеграл		dxdydz	3
		1 x y z	3

	G
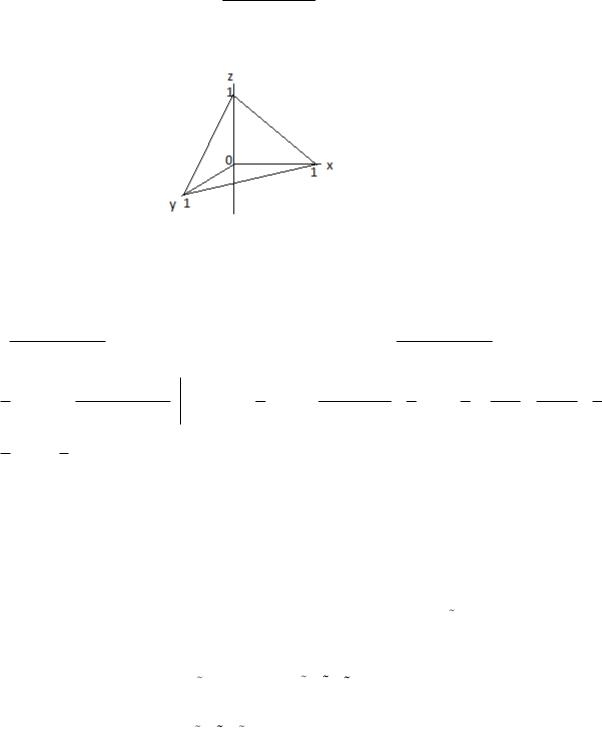
x 0, y 0, z 0, x y z 1

Решение

, где область

ограничена плоскостями

Рассматривается функция
											1/ (1 x y z)3 , (x, y, z) G
						F (x, y, z)
						F (x, y, z)						0, (x, y, z) П1,1,1 \ G										.
												0, (x, y, z) П1,1,1 \ G

Тогда по формуле вычисления интеграла по параллелепипеду
			dxdydz			1	1		1							1	1 x	1 x y				dz
			dxdydz			dx dy F (x, y, z)dxdydz dx dy																dz
		1 x y z			3	dx dy F (x, y, z)dxdydz dx dy														1 x y			z			3
G		1 x y z				0	0		0							0	0	0		1 x y			z
	1	1	1 x			1				z 1 x y			1	1	1 x		1				1		1	1			1	(1 x)	1
		1	1 x											1	1 x									1
		dx												dx
		dx						2				dy		dx					2			dy							dx
	2	0	0	(1 x y z)					z 0				2	0	0		(1 x y)				4		2	0	1 x			4	2

1 ln 2 5

2 8

2. Если

T	a,b

D

, то

F (x, y, z)dxdydz G

b
dz F (x, y, z)dxdy
a	D

(2)

Внутренний двойной интеграл берется по области

D на плоскости ХОУ при

фиксированном z и является непрерывной функцией этой переменной, которая интегрируется на отрезке a;b .

Док.

F (x, y, z)dxdy

F (x, y, z)dxdy zk

F (x, y, zk )dxdy

k 1

Пусть D

- ступенчатая область,

вписанная в D . Тогда		F (x, y, zk
вписанная в D . Тогда		F (x, y, zk
	D

являющаяся объединением прямоугольников П , ,

)dxdy F (x , y , zk ) x y o(1)	и

b		n
dz F (x, y, z)dxdy F (x , y , zk ) x y zk o(1)
a	D	i 1

Второе слагаемое справа – интегральная сумма для тройного интеграла и ее предел равен самому интегралу с одной стороны, а с другой – повторному интегралу.

3. Если

G =

	V	f ,g
	V	D
		D

, то

F (x, y, z)dxdydz

f( x, y )

dxdy F (x, y, z)dz

(3)

G	D	g ( x, y )
Внутренний одномерный интеграл берется по переменной z			при фиксированных x, y

на отрезке g(x, y); f (x, y) и является непрерывной функцией этих переменных.

Последняя функция интегрируется по области D , и полученное число представляет тройной интеграл функции F(x, y, z) по области G .

Док. Пусть

F (x, y, z)

Тогда

	m min g(
		( x, y ) D
	F (x, y, z),
		0, z m, g
		0, z m, g

x, y), M max f (x, y) и ( x, y ) D

g(x, y) z f (x, y), (x, y) D (x, y) f (x, y), M , (x, y) G

f ( x, y )

k 1

dxdy

F (x, y, z)dz dxdy

F (x, y, z)dz

g ( x, y )

k 1

F (x, y, z

)dxdy

F (x

, y

, z

) x y

o(1)

k 1

F (x , y

, z

) x y

o(1)

F (x

, y

, z

) x y

o(1)

k ,

Первое слагаемое в правой части равенства – интегральная сумма тройного интеграла

F (x, y, z)dxdydz , который существует, а левая часть равенства – повторный интеграл. G

Предельный переход при d( ) 0

Пример 3. Вычислить интеграл

доказывает формулу (3).

zdxdydz , где область G ограничена поверхностью

		h	2
конуса z	2	h		(x	2	y	2	)
	2				2		2
		R	2
			2

Решение

и плоскостью z h .

	h
zdxdydz zdz dxdy
G	0	D
		z

, где

круг

				z	2	R		2
x	2	y	2	z		R
x		y

					h		2
					h

. Во внутреннем интеграле

вычисляется площадь круга, т.е. R2 z2 h2

и
и
	G

		z	4		z h	2	h	2
			4			2		2
zdxdydz R	2					R
zdxdydz R		4h		2		4
				2
					z 0
					z 0

4. Если

G	c

, то

F (x, y, z)dxdydz G

b
dp F (x, y, p)dxdy
a	D
	p

(4)

Внутренний двойной интеграл берется по сечению области G плоскостью z p , а внешний одномерный интеграл берется по отрезку значений параметра p , при которых эти сечения не пусты.

ДОК. Разобьем отрезок a;b на отрезки pk ; pk 1 длиной pk .По теореме о среднем для одномерного интеграла на отрезке pk ; pk 1 существует точки pk pk ; pk 1 , для которых

b	n
dp F (x, y, p)dxdy	F (x, y, pk )dxdy pk . Оценим двойной интеграл с помощью
a Dp	k 1 Dp
	k
интегральной суммы:
F (x, y, pk )dxdy F (x , y , pk ) x y o(1) ,
Dp
k

построенной по ступенчатой области Dk ( ) , являющейся объединением прямоугольников Пk , , Пk , x y . Тогда повторный интеграл можно представить в виде:

n
F (x, y, pk )dxdy pk	F (x , y , pk ) x y pk o(1)
k 1 Dp	k ,
k

Выражение справа при d( ) 0 имеет предел, равный тройному интегралу, а выражение слева равно повторному интегралу.

Пример 4. Вычислить интеграл x2 dxdydz , где область G

			G
z y2 ,	z 4 y 2 ,	z x ,	z 2x , z 1,	y 0 .

ограничена поверхностями:

РЕШЕНИЕ. Буква z наиболее часто встречается в уравнениях границы, поэтому сечения следует проводить перпендикулярно оси OZ плоскостями z p . Сечением являются

прямоугольники Dp					, границы которого имеют уравнения:
x	p	,	x p ,	y	p	,	y	p , p 0;1 .
	2				2

Тогда

x	2	dxdydz

1
dp x		2	dxdy
dp x			dxdy
0	D
	p

1	p			p
dp x		2	dx	dy
dp x			dx	dy
0	p / 2			p /	2

1	7	1

3	8
		0

p	7	dp
	2

		7
		108
		108

П.3 Замена переменной в тройном интеграле.

ОПР. Заменой переменной в пространстве называют биективное отображение

Gu,v,w

G
f
	x, y,z

области

G	u ,v,w

R	3

на область

G	x, y,z

в R

, при котором каждая точка

		x x(u,v, w),
Q(u,v, w) Gu ,v,w переходит в точку
		P(x, y, z) Gx, y,z , причем y y(u,v, w),
			z z(u,v, w)


Отображение задается непрерывно дифференцируемыми функциями
x x(u,v, w) ,	y y(u,v, w) , z z(u,v, w)

	x	x	x
	u	v	w
Определитель J (u,v, w)				0	называется якобианом отображения f .
Определитель J (u,v, w)	yu	yv	yw	0	называется якобианом отображения f .
	z	z	z
	u	v	w

Пример 5 (сферическая замена переменных)

Положение точки Q в пространстве можно характеризовать тремя числами u r , v w - сферическими координатами точки. Здесь r - расстояние точки Q до точки О - начала координат r 0 . Если Q проекция точки Q на плоскость ХОУ, то - угол, который образует вектор OQ с положительным направлением оси ОХ, 0;2 .

Наконец,
Наконец,	- угол, который образует вектор OQ с плоскостью ХОУ,		;
		2
		2		2

Связь между декартовыми и сферическими координатами осуществляется по формулам :

x r cos cos ,

r sin cos , . Например, прообразом шара: x

при отображении

z r sin

сферической замены является параллелепипед r, , : 0 r R, 0 2 ,

cos cos

r sin cos

r cos sin

Якобиан сферической замены J (r, , ) sin cos

r cos cos

r sin sin

sin

r cos

= r2 sin2 cos sin

cos

r2 cos3 cos

sin

r2 cos

cos

sin

cos

 2

ЗАМЕЧАНИЕ.

Иногда в сферической замене вместо угла	используют угол		, 0; ,
		2

образуемый вектором OQ с положительным направлением оси OZ. В этом случае

соответствующая замена переменных задается формулами:

с якобианом J (r, , ) r2 sin .


	x r cos sin ,

	y r sin sin ,
		z r cos
		z r cos

Пример 6. (Цилиндрическая замена)

Положение точки Q в пространстве можно характеризовать

тремя числами

u r,

и w

называемыми цилиндрическими координатами точки

. Здесь

r - длина вектора

OQ		на плоскости ХОУ,

направлением оси ОХ,

r 0 ,0;2


- угол, который образует вектор OQ		с положительным

, и h - проекция вектора OQ	на ось OZ, h R .

Связь между декартовыми и цилиндрическими координатами осуществляется по

	x r cos ,
формулам
	y r sin ,
		z h

УПРАЖНЕНИЕ. Вычислить якобиан цилиндрической замены переменных. Ответ: J (r, ,h) r .

Прообразом прямого кругового цилиндра x, y, z : x	2	y	2	R	2	, 0	z H при

отображении цилиндрическойr, ,h : 0 r R, 0 2 , 0

замены является параллелепипед

h H .

ТЕОРЕМА 3. (О замене переменной в тройном интеграле)

Пусть функция F(x, y, z) непрерывна на замкнутой, ограниченной и измеримой области Gx, y,z . На замкнутой, ограниченной и измеримой области Gu,v,w задано отображение

x x(u,v, w),

y y(u,v, w), G

, осуществляющее биекцию области Gu,v,w на x, y,z , причем функции

z z(u,v, w)

x x(u,v, w) , y y(u,v, w) , z z(u,v, w) непрерывно дифференцируемые в точках области Gu ,v,w .Тогда имеет место формула:

F (x, y, z)dxdydz Gx , y , z

F (x(u,v, w), y(u,v, w), z(u,v, w)) J (u,v, w) dudvdw.

Gu ,v ,w

ДОК. (Без доказательства) Пример 7. Вычислить интеграл

x2 G

y	2	dxdydz

, где область

, ограничена

поверхностями x2 y2 2z , z 2

РЕШЕНИЕ. Сделаем цилиндрическую замену. Для этого подставим формулы перехода в

уравнения границы области r			2	2h	, h 2 .		Прообразом области G является область

	r, , h : 0 2 , 0 h 2, 0 r								. Тогда по формуле замены:
Gr , ,h								2h
	2	2	2h			2				16
x2 y 2 dxdydz = d dh			r 3dr			2 h2 dh					.

G	0	0	0			0	3

Приложение тройного интеграла 1. Масса тела

m(G) масса тела – аддитивная функция множества. Ее производная по множеству

(x, y, z) lim	m(U	(M ))	, гдеU (M ) шар радиуса

	U	(M )
0	U	(M )

называется плотностью распределения массы. Тогда
		m(G) (x, y, z)dxdydz
			G

с центром в точке M (x, y, z) ,

Статические моменты относительно координатных плоскостей вычисляются по формулам

M xy z dxdydz,	M xz y dxdydz,	M yz x dxdydz
G	G	G

Центр тяжести тела определяется по формулам:

m(G)

Пример 8

x	2	y	2	z
	2		2

Найти массу и координаты центра тяжести тела, ограниченного поверхностью

2	2az	с плотностью (x, y, z) k /	x	2	y	2	z	2

Решение. Перейдем к сферическим координатам в интеграле

m	kdxdydz
	x	2	y	2	z	2
G

Уравнение поверхности:

r 2a sin ,	0;		, 0; 2 ,	k
r 2a sin ,	0;		, 0; 2 ,	r
		2		r

	2		/2			2asin						k		/2	r	2	2a sin		/2					2
	2		/2			2asin								/2		2			/2					2
m(G) d				d				r	2	cos			dr 2 k cos d						2		2	d sin		4a k
m(G) d				d				r		cos		r	dr 2 k cos d		2				4a k sin			d sin		3
	0		0			0						r		0	2		0		0					3
	0		0			0								0			0		0
Вычисление момента M xy :
M		zdxdydz k						2 d / 2 cos sin d						2a sin r2dr	16 a3k			/ 2 cos sin4		d			16 a3k
M		zdxdydz k						2 d / 2 cos sin d						2a sin r2dr			3	/ 2 cos sin4		d			15
xy																	3						15
xy
	G							0		0				0				0
Тогда z			M xy		4a		,	x		y	0
Тогда z							,	x		y	0
	ц		m			5		ц		ц
			m			5

ВОПРОСЫ К ЭКЗАМЕНУ.

1.Измеримые множества в R3 . Мера множества. Примеры измеримых множеств.

2.Понятие тройного интеграла. Необходимое условие интегрируемости функции. Достаточное условие интегрируемости функции. Свойства тройного интеграла.

3.Повторное интегрирование. Вычисление тройного интеграла через повторные по стандартным областям.

4.Замена переменной в пространстве, якобиан преобразования. Формула замены переменной в тройном интеграле.

5.Сферическая и цилиндрическая замены переменных. Вычисление якобианов преобразований. Формулы вычисления тройных интегралов в сферической и

цилиндрической системе координат.

Соседние файлы в папке Лекции

#
17.05.2024353.18 Кб0VTA_lektsia_11.pdf
#
17.05.2024232.02 Кб0VTA_lektsia_12.pdf
#
17.05.2024382.65 Кб0VTA_Lektsia_13.pdf
#
17.05.2024302.83 Кб0VTA_lektsia_14.pdf
#
17.05.2024576.23 Кб0VTA_lektsia_2.pdf
#
17.05.2024450.44 Кб0VTA_lektsia_5.pdf
#
17.05.2024443.26 Кб0VTA_lektsia_7.pdf
#
17.05.2024326.27 Кб0VTA_lektsia_8.pdf
#
17.05.2024505.71 Кб0VTA_lektsia_9.pdf