
Лекции / Metodichka_Grishina (1)
.pdf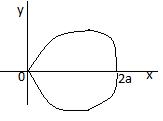
Ф-03-Лекция 3 Приложение двойного интеграла |
|
|
|||
Геометрические приложения |
|
|
|
|
|
П.1 Вычисление площади области |
|
|
|
||
Если область G измерима, то ее площадь (мера) равна |
|
||||
|
SG 1 dxdy |
|
|
||
|
|
G |
|
|
|
Действительно, интегральная сумма для функции |
f (x, y) 1 |
, |
|||
|
|||||
соответствующая разбиению |
G |
|
|
|
|
, равна сумме площадей прямоугольников, |
|||||
составляющих |
G |
|
d( ) 0 |
совпадают: один равен |
|
. Тогда их пределы при |
|
||||
площади области G , второй – двойному интегралу.
Пример 1 Вычислить площадь области ограниченной линией
x |
|
y |
|
|
|
2 |
|
2 |
2 |
|
|
|
2ax |
3 |
|
.
Решение
|
|
|
x r cos |
|
|
|
|
|
|
|
|
|
|||||
Полярная замена |
|
|
|
|
приводит к записи уравнения кривой в |
||||||||||||
y r sin |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
полярной системе: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
r |
4 |
2ar |
3 |
cos |
3 |
r 2a cos |
3 |
, |
|
|
|
; |
|
|
|||
|
|
|
|
|
2 |
2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Площадь области G равна
|
|
|
|
|
|
|
/ 2 |
|
2a cos3 |
|
|
|
/ 2 |
|
a2 |
/ 2 |
|
|
S |
|
dxdy |
d |
|
|
rdr 2a2 |
cos6 d |
(1 cos 2 )3 d |
||||||||||
|
|
|
|
|
|
|
||||||||||||
G |
|
|
|
|
|
|
|
|
|
4 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
G |
|
/ 2 |
|
|
0 |
|
|
|
/ 2 |
|
|
/ 2 |
|
|
a |
2 |
|
|
|
|
|
|
5 a |
2 |
|
|
|
|
|
|
||
|
|
|
(1 cos )3 d |
|
|
|
|
|
|
|
|
|||||||
|
|
|
8 |
|
|
|
|
|
|
|
|
|||||||
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

П.2 Вычисление объемов цилиндрических тел |
|
|
|
|
|
|||||||||
Тело C G, f , g x, y, z R3 |
: (x, y) G, g(x, y) z f (x, y) |
|
||||||||||||
назовем цилиндрическим с основанием G |
, ограниченного цилиндрической |
|||||||||||||
поверхностью с направляющей |
G |
и образующей перпендикулярной |
|
|||||||||||
|
|
|
||||||||||||
плоскости |
xoy |
, а также двумя поверхностями с уравнениями |
z g(x, y) |
и |
||||||||||
|
|
|
|
|||||||||||
z f (x, y) |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
Если область G |
измерима, а функции z g(x, y) и z f (x, y) непрерывны |
|
||||||||||||
на |
G |
, то объем цилиндрического тела C равен |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
VC f (x, y) g(x, y) dxdy |
|
|
|
|
||||||
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
G |
|
|
Действительно, рассмотрим ступенчатую область |
, вписанную в |
. Из |
|
|||||||||||
|
|
|||||||||||||
ограниченности функций |
f (x, y) |
и |
g(x, y) |
следует существование константы |
||||||||||
|
|
|
||||||||||||
N 0, для которой g(x, y) g(x, y) N 0 |
|
|
|
|
|||||||||
и |
f |
(x, y) |
f (x, y) N 0 |
, при этом объемы тел |
C |
|
G, f |
, |
|||||
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
||||||
одинаковые (параллельный перенос). Обозначим через |
|
||||||||||||
m |
(g) |
inf |
g(x, y), M |
|
(g) sup |
g(x, y), |
|
|
|
||||
|
|
( x, y ) П |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
( x, y ) П |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
( f ) |
inf |
f (x, y), M |
|
( f ) sup |
f (x, y) |
|
|
|
||||
|
|
( x, y ) П |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
( x, y ) П |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g
и |
C |
|
G, f , g
Тогда |
m |
( f ) П |
V |
|
|
|
M |
|
( f ) П |
|
|
|
C G, f ,0 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
нижняя и верхняя интегральные суммы Дарбу для G
.
f
Слева и справа стоят
(x, y)dxdy , поэтому на
основании леммы о «двух полицейских» заключаем, что
VC G, f ,0 |
f (x, y)dxdy . Аналогично,VC G,g ,0 g(x, y)dxdy |
||
|
G |
|
G |
Тогда |
|
|
|
VC VC G, f ,0 |
VC G,g ,0 f (x, y)dxdy g(x, y)dxdy |
||
|
|
G |
G |
f (x, y)dxdy g(x, y)dxdy f (x, y) g(x, y) dxdy
G G G
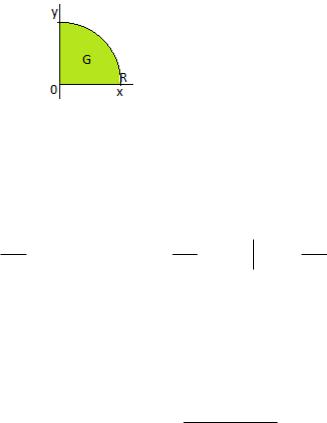
Пример 2. Вычислить объем тела ограниченного плоскостями
x 0, y 0, z 0 |
, цилиндрической поверхностью |
x |
2 |
y |
2 |
R |
2 |
и |
|
|
|
поверхностью гиперболического параболоида |
z xy |
(в первом октанте) |
|
||
Решение |
|
|
V
G
xydxdy
.
После полярной замены
x r cos |
, 0 |
|
, 0 |
r R |
|
|
|||
y r sin |
|
2 |
|
|
имеем
|
/ 2 |
R |
|
|
R |
4 |
/ 2 |
|
R |
4 |
|
|
|
/ 2 |
|
R |
4 |
V |
|
d r |
3 |
sin cos dr |
|
|
sin d sin |
|
sin |
2 |
|
|
|
||||
|
|
|
|
|
|
|
|||||||||||
|
4 |
8 |
|
0 |
8 |
||||||||||||
|
0 |
0 |
|
|
0 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
П. 3. Механические приложения |
|
|
|
|
|
|
|
|
|
|
Масса неоднородной пластины |
|
|
|
|
|
|
|
|
|
|
Дана плоская неоднородная пластина G |
с поверхностно распределенной |
|||||||||
|
|
|
|
|
m |
|
|
|
|
|
плотностью массы |
(x, y) 0 |
. Здесь |
(x, y) lim |
U |
|
(x, y) |
|
, где |
||
|
|
|
|
|||||||
|
|
|
|
|
||||||
|
|
|
|
(x, y) |
|
|||||
|
0 |
|
||||||||
|
|
|
|
U |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
U (x, y) круг радиуса 0 |
с центром в точке x, y . |
(x, y) - непрерывная функция в области G на плоскости.
Тогда масса пластины G |
при известной плотности |
|
|
Предполагается, что
(x, y) 0 |
равна |
|
G |
|
|
(x, y)dxdy |
|
|
m |
|
|
|||
|
|
G |
|
|
|
Действительно, разобьем пластину G на прямоугольные пластины |
П |
||||
|
|||||
Тогда масса прямоугольной пластины П G |
оценивается |
|
|||
inf (x, y) П m П |
sup ( x, y) П |
|
|||
( x, y) П |
|
|
|
( x, y) П |
|
|
|
|
|
|
|
G
.
Суммируя неравенства, получим

( x, y) П |
|
|
|
|
|
|
|
|
|
|
|
inf |
(x, y) |
|
П |
m G |
|
|
sup ( x, y) |
|
П |
|
|
|
|
|
|
( x, y) П |
|
|
||
Масса пластины (G)
при этом выражения
является пределом масс ступенчатых пластин m G
справа и слева являются нижней и верхней суммой
,
Дарбу интеграла
(x, G
y)dxdy
.
Статические моменты пластины относительно осей координат
M x G y (x, y)dxdy, |
M y G x (x, y)dxdy |
G |
G |
Моменты элементов разбиения
П
относительно оси
ox
M |
(П ) y |
|
x |
|
|
областиG
(x , y ) (П )
M x G
складываясь, образуют момент ступенчатой
y (x , y ) (П ) .
Последнее представляет собой интегральную сумму
G
y (x,
y)dxdy
,
поэтому после предельного перехода получим M x G y (x, y)dxdy .
|
G |
Центр тяжести пластины |
|
y (x, y)dxdy |
x (x, y)dxdy |
x |
G |
|
, y |
G |
|
|
|
|
|
||
G |
mG |
G |
mG |
||
|
|
|
|
||

По определению центром тяжести пластины называют точку с координатами
(x |
, y |
G |
G |
x xG Тогда
) такую, что статические моменты пластины относительно прямых
и |
y y |
равны нулю. |
G |
|
|
|
G |
|
|
|
|
G |
|
|
|
|
|
|
|
||
|
( y y |
|
) (x, y)dxdy 0 |
|
(x |
x |
) (x, y)dxdy 0 |
|
|
|
|
||||||
G |
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xG mG y (x, y)dxdy , |
yG mG x (x, y)dxdy |
|
|
|
|
||||||||||||
|
|
|
|
|
G |
|
|
|
|
G |
|
|
|
|
|
|
|
Пример 3. Найти статистические моменты Mx и M y |
однородной пластины в |
||||||||||||||||
|
|
|
|
|
|
|
|
|
G f |
|
|
x b, 0 y |
|
||||
форме криволинейной трапеции |
(x, y) : a |
f (x) |
|||||||||||||||
a,b |
|
|
|
|
|
|
|
||||||||||
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
b |
f ( x) |
|
1 |
b |
|
|
По условию (x, y) 1, тогда M x |
ydxdy dx |
ydy |
f 2 (x)dx |
||||||||||||||
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Gaf,b |
a |
0 |
|
2 a |
|
||
|
|
|
|
|
b |
f ( x) |
b |
|
|
|
|
|
|
|
|
||
M y |
|
xdxdy xdx |
dy xf (x)dx |
|
|
|
|
|
|
||||||||
|
|
G |
f |
|
a |
0 |
a |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
a ,b |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример 4. Найти координаты центра тяжести пластины, ограниченной
кривой эллипса
(x, y) k xy .
Решение
x a
2 |
|
y |
|
|
|
||
2 |
b |
||
|
|||
|
|
2 2
1
и осями координат (
x 0, y
0
), у которой

Для нахождения массы пластины воспользуемся обобщенной полярной
заменой
x a cos
y b sin
с якобианом
J
ab
. Тогда
|
|
|
|
|
|
|
/ 2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
kab |
/ 2 |
|
|
|
|
kab |
|
|
|||||
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
m |
k |
|
xydxdy k |
|
|
d |
|
ab |
sin cos d |
|
|
|
|
sin d sin |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
4 |
|
|
8 |
|
|
|
||||||||||||||||||||||
|
|
G |
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Вычислим статические моменты Mx |
и M y : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
/ 2 |
1 |
|
|
|
|
|
|
|
|
|
|
2 |
b |
3 / 2 |
|
|
|
|
|
2 |
b |
3 |
|
M x |
k xy |
dxdy ka |
b |
3 |
d |
4 |
sin |
2 |
cos d |
ka |
|
sin |
2 |
d sin |
ka |
|
|||||||||||||||||||
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
G |
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
5 |
0 |
|
|
|
|
|
15 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
/ 2 |
1 |
|
|
|
|
|
|
|
|
|
|
3 |
2 / 2 |
|
|
|
|
|
3 |
2 |
||||
M y |
k x |
2 |
|
|
3 |
|
2 |
|
d |
4 |
|
|
|
|
2 |
|
|
ka b |
|
|
|
2 |
|
|
ka b |
|
|||||||||
|
ydxdy ka b |
|
|
|
|
sin cos |
|
d |
|
5 |
cos |
|
d cos |
15 |
|
||||||||||||||||||||
|
|
G |
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Тогда координаты центра тяжести пластины
|
|
8ab |
2 |
|
|
|
2 |
b |
x |
|
|
, |
y |
|
8a |
||
|
|
|
|
|||||
G |
|
15 |
|
|
G |
|
15 |
|
|
|
|
|
|
|
|||
Момент инерции пластины относительно осей координат
J |
x |
(G) |
|
y2 (x, y)dxdy |
J |
y |
(G) |
|
x2 |
(x, y)dxdy |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
G |
|
|
|
|
G |
|
|
Пример 5. Найти момент инерции пластины |
G |
с распределенной на ней |
|
||||
|
|
||||||
массой с плотностью |
(x, y) |
относительно оси |
L |
, составляющей угол |
|
||
|
|
|
|||||
осью |
ox |
. |
|
|
|
|
|
|
|
||
Решение |
|
|
|
||
Сделаем замену переменных |
(x, y) (u, v) |
(преобразование поворота на |
|||
|
|||||
угол ) |
|
|
|
|
|
u x cos y sin |
|
|
|
||
|
|
|
с якобианом J 1 |
|
|
v x sin y cos |
|
||||
с

Координатная ось ей прямой.
Mu |
(G) v |
(x, y |
|
2 |
|
|
G |
|
ou расположена на оси
)dxdy x sin y cos G
L |
, а ось |
ov |
- на перпендикулярной |
|||||||||
|
|
|||||||||||
|
2 |
(x, y)dxdy cos |
2 |
J |
|
sin |
2 |
J |
|
|
||
|
|
|
||||||||||
|
|
x |
|
y |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||
2sin cos K |
xy |
|
Здесь число |
K |
xy |
(G) |
|
xy (x, y)dxdy |
называется центробежным моментом |
||||
|
|
|
|
|||||||
|
|
|
|
|
G |
|
|
|
|
|
Пример 6. Плоская пластина G с распределенной на ней массой с |
|
|
||||||||
плотностью |
(x, y) |
расположена в пространстве и вращается вокруг оси |
oy |
с |
||||||
|
|
|
|
|||||||
угловой скоростью (рис). Найти величину возникающей при этом |
|
|
||||||||
центробежной силы и ее момент относительно оси |
oz |
|
|
|||||||
|
|
|
||||||||
(моменты относительно других осей равны нулю).
Выделенный прямоугольник
П
Рис
имеем массу
m
, расположенную в
пределах
inf |
(x, y) (П ) m |
|
( x, y ) П |
|
|
|
|
|
|
sup |
|
( x, y ) П |
|
|
(x,
y) (П
)
, создает при
вращении центробежную силу F |
2 x m . После суммирования по , |
||||||||||||||
получим |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|||
|
|
|
x |
inf |
(x, y) (П ) |
|
|
F |
|
|
|
|
x |
sup |
(x, y) (П ) |
|
|
|
|
( x, y ) П |
|
|
|
|
|
|
|
|
|
( x, y ) П |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Наконец, предельный переход при d( ) 0 с учетом того, что справа и слева стоят суммы Дарбу интеграла 2 x (x, y)dxdy , приводит к ответу
G
F |
x (x, y)dxdy |
|
M y |
2 |
|
2 |
|
G |
|
|
|
Для момента центробежной силы относительно оси oz имеем выражение
M F |
|
xy (x, y)dxdy |
|
Kx, y |
|
2 |
|
2 |
|
|
G |
|
|
|

Лекция по теме «Площадь поверхности» П.1 Поверхности в пространстве. Площадь поверхности.
ОПР. Гладкая поверхность S |
в пространстве R |
3 |
задается параметрическими уравнениями |
|
в векторной форме r r(u, v), u, v Duv , где Duv - замкнутая измеримая область на плоскости
|
|
x x(u,v), |
|
|
|
|
|
переменных (u,v) или в координатной форме y y(u,v), (1) |
|||
|
|
|
z z(u,v) |
|
|
|
|
|
|
|
|
с заданными функциями |
x(u,v), |
y(u,v), z(u,v), имеющие непрерывные частные производные |
|
первого порядка в
Duv
.Через Dxy обозначим образ области Du ,v
при отображении
xy
x(u, v) y(u, v)
.
Уравнение поверхности может быть задано явно, например, z f (x, y), (x, y) Dxy (2)
Она называется гладкой, если функция f (x, y) имеет непрерывные частные производные в области Dxy . Уравнение поверхности (2) можно записать в параметрической форме (1):
|
x u |
|
|
y v |
|
|
||
|
z f (u, v) |
|
|
||
|
Поверхность S |
не имеет особых точек, если |
r r |
|
A; B;C |
|
|
|||
|
u |
v |
|
|
|||||
|
|
|
: |
|
|
|
|
|
|
координаты векторного произведения ru |
rv |
|
|
|
|
|
|
||
0, (u; v) Duv
. Здесь
A, B,C
-
A |
y |
z |
, |
B |
x |
z |
, C |
x |
y |
|
u |
u |
u |
u |
u |
u |
|||||
|
|
|
|
|||||||
|
y |
z |
|
|
x |
z |
|
x |
y |
|
|
v |
v |
|
|
v |
v |
|
v |
v |
(3)
Вектор n (x, y, z) A; B;C называется нормалью к поверхности S в точке (x; y; z) на |
|
|
|
|
||||||||||||||||
поверхности. Ее длина и направляющие косинусы вычисляются по формулам: |
|
|
|
|
||||||||||||||||
n |
2 |
B |
2 |
C |
2 |
, cos |
A |
|
|
|
; cos |
B |
|
|
|
; cos |
C |
|
|
|
A |
|
|
B |
|
C |
|
B |
|
C |
|
B |
|
C |
|
||||||
|
|
|
|
|
|
A |
|
|
A |
|
|
A |
|
|
||||||
|
|
|
|
|
|
2 |
|
2 |
|
2 |
2 |
|
2 |
|
2 |
2 |
|
2 |
|
2 |
Гладкая поверхность S называется односторонней, если на ней существует точка M и непрерывный замкнутый путь, проходящий через точку M S , такой, что при движении вдоль этого пути из точки A в точку A непрерывная нормаль меняет свое направление на противоположное.
