Добавил:

okley Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский ядерный университет (МИФИ)

Предмет:

Векторный и тензорный анализ

Файл:

Лекции / Metodichka_Grishina (1)

.pdf

Скачиваний:

Добавлен:

17.05.2024

Размер:

6.66 Mб

Скачать

☆

<<< < Предыдущая 12 / 112 3 4 5 6 7 8 9 10 11 > Следующая >>>

По формуле (4):

П0,1

0,1

1	1	1	1	1	1	1

xydxdy	xydy dx x ydydx			2	xdx	4
0	0	0	0		0

(см пример 1)

ТЕОРЕМА 4. (О вычислении двойного интеграла по стандартной области)


Если функция					F(x, y)	непрерывна в стандартной области
Если функция						непрерывна в стандартной области
K	a,b	( f , g, x)			x, y : a x b, g(x) y f (x)			f (x), g(x)	-
	a,b						, где функции		-
непрерывны на отрезке						a;b	, то двойной интеграл функции	F (x, y) по
непрерывны на отрезке							, то двойной интеграл функции	F (x, y) по
области			K	a,b можно вычислять по формуле:
области				a,b можно вычислять по формуле:

F (x, y)dxdy Ka ,b

F (x, y)dy dx

f ))(( xxgab

(5)

Если функция F(x, y) непрерывна в стандартной области

с,d

( , , y)

x, y : c y d, ( y) x ( y)

, где функции

( y), ( y)

- непрерывны на

отрезке c;d , то двойной интеграл функции F(x, y) по области

c,d

можно

вычислять по формуле:

d ( y )

(6)

F (x, y)dxdy

F (x, y)dy dx

Kc ,d

c ( y )

ДОК. Докажем формулу (5). Пусть

А min g(x)

B max

f (x)

x a;b

F (x, y), (x, y) Ka,b

Рассмотрим функцию

F (x, y)

A,B

\ K

Она кусочно-

0, (x, y) П

a,b

A,B

F (x, y)dxdy

непрерывна на

a,b и на основании формулы (5):

A,B

a ,b

f ( x)

F (x, y)dy

F (x, y)dxdy = F (x, y)dy

Ka ,b

a A

a g ( x)

Формула (6) доказывается аналогично (самостоятельно).

Пример 4. Вычислить интеграл			x ydxdy		, гдеG

		G
ограниченный прямыми x 0	,	y 0		и x y 1

РЕШЕНИЕ. По формуле (5)

- треугольник,

	x
G

ydxdy

1	1 x
dx		x ydy
0	0

	1		3
3			3
3
2		x y	2	y 1 x	dx
		x y	2	y 0	dx
	0

2	1		3		2		2		5			2
2	1				2		2				x 1	2
			2						2		x 1
3	1	x		dx	3	x	5	x		x 0			.
3	0				3		5					5
	0

УПРАЖНЕНИЕ. Докажите формулу Дирихле

a	x	a	a
dx f (x, y)dy dy
0	0	0	y

(x,

y)dx

ВОПРОСЫ К ЭКЗАМЕНУ.

1. Измеримые множества, мера множества. Примеры измеримых множеств. 2.Понятие двойного интеграла. Необходимое условие интегрирования. 3.Теорема об интегрируемости непрерывной функции на измеримом множестве.

4.Свойства двойного интеграла.

5.Повторное интегрирование. Вычисление двойного интеграла по прямоугольнику.

6.Вычисление двойного интеграла по стандартной области.

Ф-03-Лекция 2 Замена переменной в двойном интеграле

П.1 Линейная замена в двойном интервале.

x au bv
Отображение		, ad bc 0
y cu	dv
прообраз области Gx, y	на плоскости xoy

функции f (x, y) имеет место формулаf (x, y)dxdy f (au

называется линейной заменой переменных. Если

при таком отображении, то для непрерывной на

bv, cu dv) ad bc dudv (1)

G
	u ,v
G	x, y

G	G
x , y	u ,v

Док.

Образом прямой при линейном отображении является прямая, образом квадрата ABCD разбиения области Gu ,v со стороной h является параллелограмм PQRT . Координаты вектора

h; 0

и его образа

ah; ch

. Координаты вектора

0; h

и его образа

bh; dh

. Площадь

PQRT

i	j	k
	ch	0	ad bc h	2
равна ah	ch	0	ad bc h
	dh	0
bh	dh	0

M произвольная точка квадрата, N

- ее образ в параллелограмме

PQRT

Интегральная сумма для интеграла f (x, y)dxdy равная f (N ) ad bc h2 является

Gx , y

i, j

интегральной суммой для интеграла

Gu ,v

f (au bv, cu dv) ad

bc dudv

. Из равенства

интегральных сумм следует равенство интегралов после предельного перехода при h 0 .

	x2dxdy по области G		R2 : y x 2, 2
Пример 1. Вычислить интеграл		x; y		x y 4

Решение

Замена переменных:

y x

x (v u) / 2

(u; v) R2 : 2 u 2, 2 v 4 , J

1/ 2

u,v

x y

y (u

v) / 2

1/ 2

Тогда по формуле замены переменных

(u v)

u 2

dxdy

dudv

dv (u v)

(u v)

u 2

u ,v

v 4

(2 v)(2

v) (2 v)

4v)

v 2

П.2 Нелинейная замена переменной в двойном интеграле.

Рассмотрим функцию f (x, y) непрерывную на измеримом множестве Gx, y .

ОПР. Заменой переменных называют биективное отображение u;v x, y ,

области Gu,v на плоскости переменных u, v

на область Gx, y

плоскости x,y ,

переводящее внутренние точки области Gu,v во внутренние точки области Gx, y , а

границу Gu ,v в границу

Gx, y

. Это отображение задается векторнозначной функцией

x x(u,v),

u, v

r r(u,v)

или в координатной форме

y y(u,v)

Если функции x x(u,v) и y y(u,v)

двух переменных имеют непрерывные частные производные

первого порядка в области Gu ,v , то замена называется гладкой. В этих предположениях кусочно-

гладкая граница Gu ,v переходит в кусочно-гладкую границу Gx, y .

Пусть Gu ,v ( ) вписанная в Gu ,v ступенчатая область, состоящая из квадратов со стороной h.

Один из таких квадратов обозначим через Пi, j (h) u,v : ui u ui

h, v j v v j

h , где

ui ,v j - координаты левой нижней вершины квадрата. Образом квадрата Пi, j (h) при отображении r является измеримая область Gi, j (h) с кусочно-гладкой границей, состоящая из внутренних точек Gx, y .

Лемма 1 Оценка площади сегмента

Если функция

f (x)

имеет две производные на отрезке

a; a

, то площадь сегмента

(h) o(h

)

a h

f (a h) f (a)

Док. S(h)

f (x)

(x a) f (a) dx .

Разложим функцию S(h) по формуле Маклорена:

f (a h) f (a)

a h

S(0) 0, S (h)

f (a h)

h f (a)

f (a h)h f (a h) f (a)

(x a)

x a h

f (a

h)h

x a

S (h) f (a h)h f (a h) f (a h)

f (a h) h

h 0

S(h) o(h

) .

Следующая лемма оценивает ее меру.

ЛЕММА 2.



a)	f (a h)h f (a h) f (a)		dx
	h	2

f (a h) f (a)	h 0	0
	h 0

. Тогда по формуле Маклорена

(Gi, j (h)) J (ui ,v j ) h	2	o(h	2	) ,

	x	x
где J (u,v)	u	v	- якобиан отображения r
где J (u,v)	y	y	- якобиан отображения r
	y	y
	u	v

ДОК. По лемме 1 мера области Gi, j (h) отличается от площади четырехугольника ABCD с

вершинами A r(ui ,v j ) , B r(ui ,v j h) , C r(ui h;v j h) ,

D r(ui h, v j ) на величину порядка o(h2 ) .Оценим площадь SABCD = SABC SADC

S ABC	1	x(ui h,v j h) x(ui ,v j h)	y(ui h,v j h) y(ui	,v j	h)	=
		x(ui ,v j ) x(ui ,v j h)	y(ui ;v j ) y(ui ,v j	h
	2

1h2 xu (c1 ,v j h)

2xv (ui ,c3 )

=h2 J (ui ,v j ) o( 2

Аналогично, S ADC

y			(c		2		,v
		u			2
	y					(u		i
				v				i
h	2	) .
h		) .
				h		2
				h			J
				2			J
				2

jh)

,c4 )

(u	,v
i

		h	2
		h
		2
		2

j	) o(h

x	(u	,v
u	i
x	(u	,v
v	i

2	)

j j

) o(1)	y	(u	,v
	u	i
) o(1)	y	(u	,v
	v	i

j j

	) o(1)
	) o(1)
	) o(1)

Знак	выбирается с расчетом, что площадь была положительной. Тогда

(Gi, j (h)) J (ui ,v j ) h	2	o(h	2	) .

ТЕОРЕМА (формула замены переменной в двойном интеграле)

Пусть функция f (x, y) непрерывна в замкнутой измеримой области Gx, y .На замкнутой

x x(u,v),	,
измеримой области Gu,v задано кусочно-гладкое отображение	,
y y(u,v)
осуществляющее биекцию Gu,v Gx, y . Тогда
f (x, y)dxdy = f (x(u,v), y(u,v)) J (u,v) dudv .

Gx , y

Gu ,v

ДОК. С учетом утверждения леммы интегральная сумма для интеграла

f (x, y)dxdy

x , y

f (r(u

)) (G

(h))

f (r(u

)) J (u

) (П

i, j

(h)) o(1) (Gu,v )

i, j

Первое слагаемое справа является интегральной суммой для интеграла

(7)

Gu ,v

(x(u, v),

y(u, v)) J (u, v) dudv

. По условию теоремы, при

обе интегральные суммы

имеют пределы, равные соответствующим интегралам, а из равенства (7) следует, что эти интегралы равны.

ПРИМЕР 2. Вычислить интеграл

y x, y 4x, x 0, y 0.

	dxdy
	x	2	y	2
G

, где G - область с границей xy 1, xy 2,

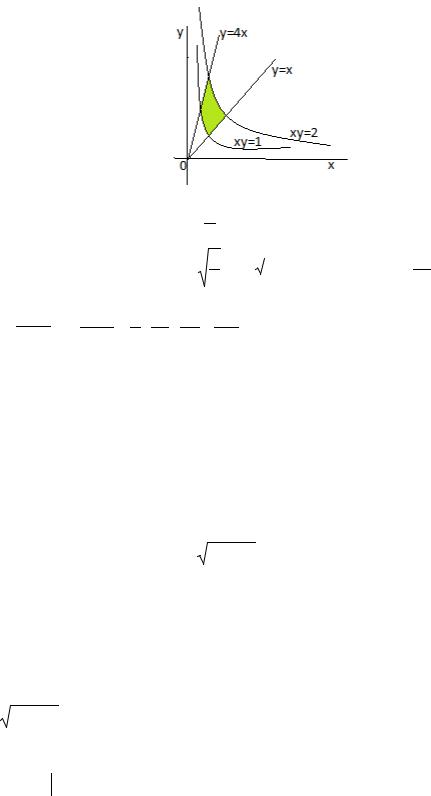
РЕШЕНИЕ. Сделаем замену u xy , v

. Тогда область Gu ,v = (u;v) :1 u 2,1 v 4 -

прямоугольник. Обратная замена x

, y

uv и якобиан J (u,v)

dxdy

dudv

ln 4

Тогда

u ,v

Полярная замена переменных Для областей, граница которых является окружностью или ее частью, употребляют ПОЛЯРНУЮ

x r cos ,	, якобиан которого
замену переменных	, якобиан которого
y r sin .

	x	y	cos	sin
	x	y	cos	sin
J (r, )	r	r			r .
J (r, )	x	y	r sin	r cos	r .
	x	y	r sin	r cos

ПРИМЕР 3. Вычислить интеграл

sin

dxdy , где Gx, y

(x, y) :

x , y

кольцо на плоскости переменных x, y .

РЕШЕНИЕ.

Gr ,

(r, ) : r 2 ,0 2 - прямоугольник на плоскости

переменных r, :

sin

dxdy

= r sin rdrd

d r sin rdr

Gx , y

Gr ,

2 r cosr

cosrdr 6

Обобщенная полярная замена

x a r cos

, r 0,

0; 2 называется обобщенной полярной заменой.

Замена

y b r sin

2

Ее

якобиан

a r

cos

b r

sin

J (r, )

ab r

2 1

sin

cos

a r

cos

sin

b r

sin

cos

Пример 4.

Вычислить интеграл

xydxdy

, где


G	(x; y) R2 :	x	y	a

	xy dxdy 4	xydxdy
G	G

Тогда граница области

Сделаем замену

	x ar cos	4

		4
	y ar sin

с якобианом

2	3	3
4a	r sin	cos

	x		y	a	a	r cos	2

G		(r, ) : 0 r 1, 0

r ,

Тогда

a	r sin	2		a

2 - прямоугольник,

r	a		r 1 r 1
xy ar sin		2	cos	2
xy ar sin			cos

Область

																								1		/ 2						a	3	/ 2
		xydxdy				4a			r	2	sin	5		cos					5	drd 4a			3	r	2	dr	sin	5	cos	5	d	a		sin	5	2 d
								3		2		5							5				3		2			5		5					5
G					G																			0		0						24		0
G					G																			0		0								0
					r ,
	a	3				a	3	1													a	3
	a		sin	5	tdt	a		(1 u					2		)	2	du				a
				5									2			2
	48					48															45
	48		0			48		1													45
			0					1
																		4a		3
			xy dxdy 4						xydxdy									4a
			xy dxdy 4						xydxdy									45
G						G												45
G						G

П.3 Формула Грина для двойного интеграла

Рассмотрим двойной интеграл по криволинейной трапеции Ka,b ( , , x) от частной производной функции f (x, y) по переменной y :

f	dxdy b	dx ( x)	f	dy b	f ( (x)) f ( (x)) dx b	f ( (x))dx a	f ( (x))dx
y			y
K	a	( x)		a	a	b

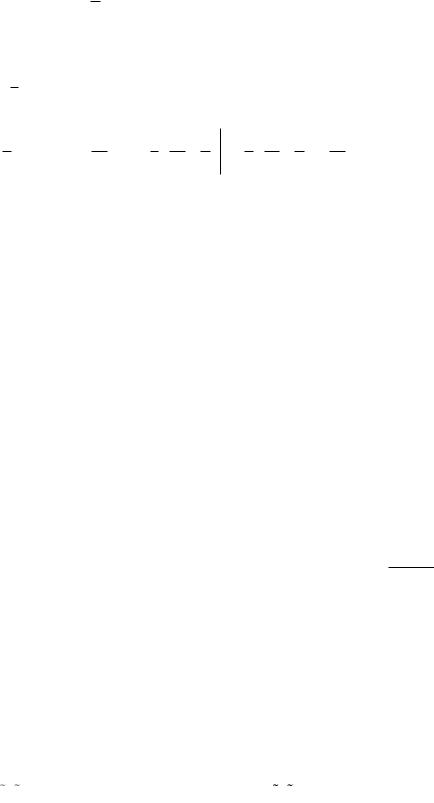
Пример 5

Вычислить двойной интеграл

xy	2	dxdy
xy		dxdy
K

по области

						2	:1 x 2,								1
K (x, y) R							:1 x 2,								x	y x
															x
Решение
Если	f (x, y)			1			xy	3	, то xy					2			f	. Тогда по формуле Грина
Если	f (x, y)			3			xy		, то xy								y	. Тогда по формуле Грина
				3													y
			1		2										1				1	x	5	1	2	1	31	1	19
					2																5
xy	2											3
xy		dxdy	3				x x						x		x	3	dx		3			x			5		10
K			3		1										x				3	5		x	1	3	5	2	10
																							1
П. 5 «Дифференцирование» интеграла по области.
Пусть g - произвольная измеримая подобласть G . Числовую функцию F(g)																												назовем аддитивной
по g , если g g1								g2 , где g1 и g2											пересекаются только по границе, выполняется равенство
F(g) F(g ) F(g										2	)
		1								2

Например, 1)	F(g)
2)	F (g)

S(g)

f (x,

площадь области

y)dxdy ;

;

G область с поверхностно распределенной массой,

F(g)

масса области g ;

G область с поверхностно распределенным давлением, F(g)

давление на

область g .

Пусть M фиксированная точка области G , а gM G - произвольная измеримая область,

содержащая M .

Производной функции F(g) по области в точке M называют предел

lim

F (g

)

f (M )

, если

)

( g ) 0

он существует.

Например, для F(g) S(g)

ее производная по области равна f (M ) 1 и Sg

1 dxdy

Покажем, что если F (g)

f (x, y)dxdy с непрерывной функцией f (x, y) в области G , то ее

производная по области в точке M (x, y) равна f (x,

Действительно, по теореме о среднем

F (gM ) f x, y (gM ) lim	F (gM )	lim
	(gM )
( gM ) 0		( gM ) 0

y) .

f x, y f (x, y)

В этом смысле двойной интеграл является «первообразной» подынтегральной функции.

Если через (x, y)

обозначить производную по области функции F(g)

из примера 3, то ее

называют поверхностной плотностью и масса пластины g вычисляется с использованием интеграла

m (x, y)dxdy

В примере 4 давление на пластину

определяется интегралом

p(x, y)dxdy

, где функция

p(x,

удельного давления – производная функции

F(g)

по области.

П.6 Двойной интеграл с переменным верхним пределом. Формула Ньютона-Лейбница для прямоугольника.

Рассмотрим двойной интеграл от непрерывной функции

f (u, v)

по прямоугольнику с

		c, y	:	F (
переменными длинами сторон Пa,x			:	F (
Тогда
x	y		y
x			y
F		f (x, v)dv,	F
	c

	x y
x, y) f (u, v)dudv
	a c
x		xy
		xy
	f (u, y)du,	F	f (x, y)
a

					x		y
Действительно, при фиксированном y			производная функции F (x, y)			du		f (u, v)dv
Действительно, при фиксированном y			производная функции F (x, y)			du		f (u, v)dv
					a		c
	y
		f (x, v)dv . При повторном дифференцировании по y					f (x, y) .
Fx		f (x, v)dv . При повторном дифференцировании по y		получим Fxy			f (x, y) .
	c

Тогда

2 F

f (x, y)dxdy

dxdy dx

(x, d )

(x, c) dx

x y

c ,d

a ,b

(x, c)dx F (b, d ) F (a, d ) F (b, c) F (a, c)

(x, d )dx

по

равна

Последняя формула является аналогом формулы Ньютона-Лейбница для одномерных интегралов Римана.

Вопросы к экзамену

1. Линейная замена в двойном интеграле. Формула для вычисления двойного интеграла с помощью линейной замены.

1. Нелинейная замена переменной в двойном интеграле, якобиан преобразования. Формула для вычисления двойного интеграла с помощью замены переменных.

2. Полярная замена переменной. Обобщенная полярная замена. Примеры.

<<< < Предыдущая 12 / 112 3 4 5 6 7 8 9 10 11 > Следующая >>>

Соседние файлы в папке Лекции

#
17.05.2024567.13 Кб0F-03-Lektsia_1.pdf
#
10.01.2025233.11 Кб0Materialy_k_lektsii_Ryady_Furye.docx
#
10.01.2025169.96 Кб0Materialy_k_lektsii_Ryady_Furye_2.docx
#
17.05.20246.66 Mб2Metodichka_Grishina (1).pdf
#
17.05.2024353.18 Кб0VTA_lektsia_11.pdf
#
17.05.2024232.02 Кб0VTA_lektsia_12.pdf
#
17.05.2024382.65 Кб1VTA_Lektsia_13.pdf
#
17.05.2024302.83 Кб0VTA_lektsia_14.pdf
#
17.05.2024576.23 Кб0VTA_lektsia_2.pdf