Добавил:

okley Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский ядерный университет (МИФИ)

Предмет:

Векторный и тензорный анализ

Файл:

Лекции / VTA_lektsia_12

.pdf

Скачиваний:

Добавлен:

17.05.2024

Размер:

232.02 Кб

Скачать

☆

Ф-03-Лекция 12. Знакопеременные ряды. П.1 Абсолютная и условная сходимости.


ОПР. Ряд an	(1) называется абсолютно сходящимся, если сходится ряд
n 1

составленный из модулей членов ряда (1). Теорема 1. Абсолютно сходящийся ряд сходится.

ДОК. Если ряд (2) сходится, то по критерию Коши:

 an

n 1

(2),

0 N

Поскольку

a	n	a	n 1	... a	m
	n		n 1		m

a	n

: n N , m n

an 1 ... am

a	n	a	n 1

, для ряда(1)

... am

выполняется критерий Коши и ряд

сходится.

Любой из достаточных признаков сходимости рядов с положительными членами может быть использован как достаточный признак абсолютной сходимости знакопеременного ряда. Например, ПРИЗНАК ДАЛАМБЕРА абсолютной сходимости знакопеременного ряда.

Если для общего члена

a	n

знакопеременного ряда

an

n 1

(1) выполняется одно из условий:

		a	1
1.	n0 , : 0 1: n n0	n
		a

		n

;

2.	lim
	n

a	1
n
a	n

, то ряд (1) абсолютно сходится.


ОПР. Числовой ряд an (1) называется условно сходящимся, если (1) сходится, а ряд
n 1

an (2), составленный из модулей его членов, расходится.
n 1
		x	n

Пример 1. При каких x			?
Пример 1. При каких x	сходится ряд n!		?
	n 1	n

Применим признак Даламбера для установления абсолютной сходимости:

an 1

(n 1)! x n 1 nn

1 n

1 x e; e

1)n 1 x

n 1

При

ряд сходится абсолютно. При x e

ряд расходится по невыполнению

необходимого признака. При x e

n 1

. Из условия монотонного возрастания последовательности

следует, что an 1 1и общий член к нулю не стремится. an

Чтобы понять разницу между абсолютной и условной сходимостями числовых рядов докажем теорему, утверждающую, что члены абсолютно сходящегося ряда можно менять местами без потери сходимости и изменения суммы ряда. Условно сходящиеся ряды при изменении порядка слагаемых могут изменять свою сумму.

Теорема 2. (Дирихле)


Пусть ряд	an	(1) сходится абсолютно и m1, m2 ,..., mn ,... любая перестановка множества
	n 1

натуральных чисел. Тогда ряд bn			(3) с общим членом bn	am	также сходится
					n
		n 1

абсолютно и имеет ту же сумму.

ДОК. Для каждой частичной суммы n

сумма m(n) a1 a2 ... am(n) ряда



n 1

b	b
1	2

a	n	, (2)
	n


... bn	ряда bn	, найдется частичная
	n 1

, включающая все слагаемые суммы n . В

свою очередь,

найдется частичная сумма

	N (n)

ряда bn , содержащая все

n 1

слагаемые суммы m(n) . Тогда n

m(n)

N (n) . Из абсолютной сходимости ряда (1)

следует, что частичные суммы m(n)

имеют предел, а поэтому ограничены. Тогда в силу

неравенства ограничены частичные суммы

и ряд (3) сходится абсолютно. Пусть S 1

, S

и Sn частичные суммы рядов (1), (2) и (3) соответственно и S –сумма ряда (1).

Тогда из абсолютной сходимости ряда (1) следует, что

0 N : m N , n m SN S

, Sn Sm

Существует число p p N такое, что для любого m p

содержит

частичная сумма Sm

первые N членов ряда (1) и поэтому

Sm S N содержит сумму членов ряда (3) с номерами

большими N, что по выбору числа N означает S

S 3

.Тогда

S S 3

S S 1 S 1

S 3

т.е. суммы рядов (1) и (3) совпадают.

Для условно сходящегося ряда справедлива

Теорема 3. (Риман) (без доказательства)

, существует

Если ряд an (1) сходится условно, то для любого числа

n 1

перестановка членов ряда (1), при которой он сходится и имеет сумму . П.2. Знакочередующиеся ряды. Признак Лейбница. Оценка остатка ряда.

Опр. Пусть

a	n

числовая последовательность. Ряд


( 1)	n 1	an
( 1)		an
n 1

(4) называется

знакочередующимся.

Теорема 4. (признак Лейбница)

Если последовательность an , an 0 монотонно убывающая и lim an 0 , то ряд (4)

n 1 n

сходится. Док.

S2k 1 a1 (a2 a3 ) (a4 a5 ) ... (a2k a2k 1) a1 , поскольку каждая из скобок неотрицательная. Тогда все частичные суммы ряда (4) с нечетными номерами ограничены. Ограниченными являются также и частичные суммы с четными номерами, поскольку S2k S2k 1 a2k 1 S2k 1 a1 . Кроме того, последовательность S2k монотонно

возрастающая:

S2k (a1 a2 ) (a3 a4 ) ... (a2k 1 a2k ) S2k 2 , k N

На основании теоремы Вейерштрасса последовательность S2k				имеет предел S	. Тогда тот
же предел имеют и частичные суммы с нечетными номерами, поскольку S2k 1					S2k a2k 1

Для знакочередующихся рядов остаток ряда ( 1)	k	ak 1	также является
Для знакочередующихся рядов остаток ряда ( 1)		ak 1	также является
k m

знакочередующимся рядом с суммой Rm

, поэтому Rm

am 1

. Последнее неравенство

называется оценкой остатка знакочередующегося ряда: отбрасывание из ряда всех слагаемых с номерами большими m приводят к ошибке вычисления суммы ряда меньшей модуля первого отброшенного члена.

				( 1)		n
Пример 2. При каких x сходится ряд				( 1)		?
Пример 2. При каких x сходится ряд				n	x	?
					x
			n 1
			n 1
При x 0 последовательность	1		монотонно стремится к нулю и ряд сходится по
При x 0 последовательность	n	x	монотонно стремится к нулю и ряд сходится по
		x

признаку Лейбница. При x 1	сходимость абсолютная.

Замечание. Требование монотонности в признаке Лейбница существенно.

					( 1)	n 1
					( 1)
Действительно, ряд					n
				n 1	n
n :	1	1	0	, а для нечетных
n :	n	n	0	, а для нечетных
	n	n

монотонности.

П.3. Преобразования АБЕЛЯ

1 n 1 n

знакочередующийся, поскольку для четных
знакочередующийся, поскольку для четных

	1	0	, но расходящийся, поскольку нет
	n	0	, но расходящийся, поскольку нет
	n

Рассмотрим преобразование конечной суммы

m ak bk

, которое связывают с именем Абеля.

k 1

Для любых чисел ak

и bk , k 1, 2,..m справедливо представление:

m 1

ak bk

am Bm ak Bk ,

k 1

ak 1 ak

b1 b2

... bk

где ak

ДОК. (индукцией по числу m )

При m=2 формула справедлива: a1b1

a2b2 a2

(b1 b2 ) (a2

a1 )b1

Предположим, что формула верна для m и докажем ее справедливость m+1:

m 1

a b

m 1 m 1

m m

m 1 m 1

k 1

Bk + am 1 am Bm = am 1Bm 1

Bk .

- ak

k 1

Теорема 5. (Признак АБЕЛЯ).

Пусть 1) ряд

сходится 2) последовательность b

монотонна и ограничена. Тогда

n 1

ряд an bn

(5) сходится.

n 1

ДОК. Воспользуемся преобразованием Абеля для оценки отрезка ряда (5):

m 1

ak bk

bm an

an 1

... am

bk 1

bk an an 1

... ak

(@)

k n

Для любого 0 N : n N , m n an an 1

... am

и bm bn

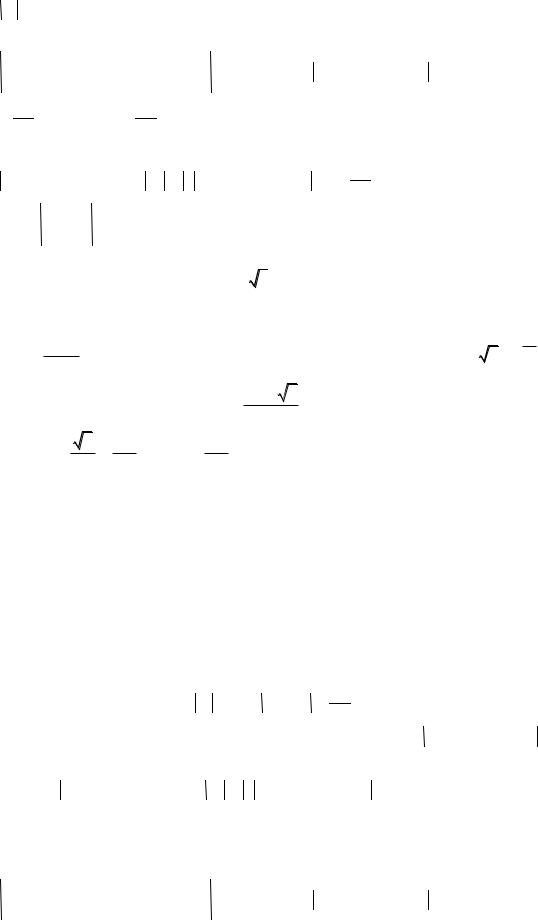
Здесь константа B 0

ограничивает значения модулей членов последовательности bn :

B для все n . Пусть последовательность b монотонно растет:

bk 1

0 (в противном случае (bk 1

bk ) 0 ). Тогда второе слагаемое оценивается

m 1

(bk 1

bk )(an

an 1

... ak )

(bk 1

bk ) an

an 1

... ak

k n

m 1

bk 1 bk

(bm bn ) .

Первое слагаемое оценивается:

bm (an

an 1 ... am )

bm an

an 1 ... am

Тогда

ak bk

для всех n N, m n и для ряда(5) выполняется критерий

k n

Коши, что завершает доказательство теоремы.

( 1)n n n

Пример 3.

Исследовать ряд

на сходимость.

ln n

n 2

Применим признак Абеля:

( 1)

ln n

Ряд

сходится по признаку Лейбница, последовательность bn

n e

ln n

n 1

( 1)

n n

монотонная и ограниченная. Ряд

сходится. Абсолютной сходимости нет,

ln n

поскольку

, а ряд

расходится.

ln n

n 2

Теорема 6. (Признак Дирихле)

Пусть

1) частичные суммы Sm an

ограничены;

n 1

2) последовательность bn монотонно стремится к нулю.

Тогда ряд

an bn

сходится.

n 1

ДОК. Воспользуемся преобразованием Абеля (@).

Тогда

0 N : n N , m n b

, b

2 A

где

– константа, ограничивающая значения отрезков ряда

n 1

... a

A, n, k

Первое слагаемое в (@) оценивается:

b (a

... a

) b

... a

A .

n 1

2 A

Второе слагаемое, с учетом знакопостоянства bk 1 bk

0 для всех k ,

(монотонность bn ), (или (bk 1 bk ) 0 ) оценивается:

m 1

(bk 1

bk )(an

an 1

... ak )

(bk 1

bk ) an

an 1

... ak

k n

	m 1
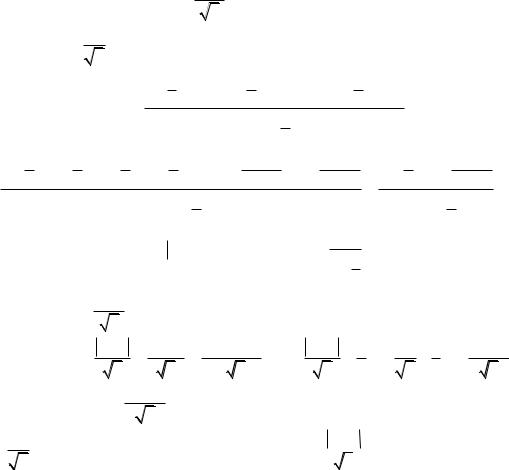
	m 1
A bk 1 bk A(bm bn ) .
	k n												2
	k n
			m


Тогда			ak bk			2		2			для всех n N, m n										и для ряда выполняется критерий Коши,
			k n			2		2
что завершает доказательство теоремы.
													sin n
Пример 4. Исследовать ряд													sin n		на сходимость.
Пример 4. Исследовать ряд														n	на сходимость.
											n 1			n
					1																								m
an	sin n, bn				1	0			. Докажем ограниченность частичных сумм ряда sin n :
an	sin n, bn					0			. Докажем ограниченность частичных сумм ряда sin n :
					n																								n 1
																													n 1
										sin	1	sin1 sin					1	sin 2 ... sin				1	sin m
										sin	2	sin1 sin					2	sin 2 ... sin				2	sin m
sin1 sin 2 ... sin m											2						2					2
sin1 sin 2 ... sin m																			1
																		sin	1
																		sin	2
																			2
	cos	1	cos	3	cos		3		cos		5	...		cos		2m 1				cos	2m 1			cos	1	cos		2m 1
	cos	2	cos	2	cos		2		cos		2	...		cos				2		cos	2			cos	2	cos			2
		2		2			2				2							2			2				2				2
													1														1
										2sin			1													2sin	1
										2sin			2													2sin	2
													2														2

Тогда справедлива оценка sin1 sin 2 ...

	sin n
Дирихле ряд	sin n	сходится. Докажем,
Дирихле ряд	n	сходится. Докажем,
n 1	n		sin		n	1 cos 2n
	sin n		sin	2	n	1 cos 2n
				2
Действительно,	n			n		2 n
	n			n		2 n

sin m

для всех m

.Тогда по признаку

sin

что сходимость ряда условная.

sin n

cos 2n

n 1

			cos 2n
Сходимость ряда			cos 2n	доказывается аналогично, обобщенный гармонический ряд
Сходимость ряда			n	доказывается аналогично, обобщенный гармонический ряд
		n 1	n
	1			m		n
	1	расходится, поэтому частичные суммы			sin	n	неограниченные и абсолютной

	n					n
n 1	n			n 1		n

сходимости ряда нет П.4. Общая схема исследования числового ряда.

1.Проверяют выполнение необходимого признака сходимости. Если он не выполнен, исследование закончено - ряд расходится.

2.Выясняют, является ли данный ряд знакоопределенным? (все члены положительные или отрицательные). Если да, то подбирают подходящий достаточный признак (сравнения с известным рядом, Даламбера, радикальный или интегральный Коши, Раабе и др.).

3.Если ряд знаконеопределен, то рассматривают ряд из модулей его членов и подбирают подходящий достаточный признак абсолютной сходимости. Если ряд из модулей сходится, то исследование заканчивается – ряд сходится абсолютно.

4.Если ряд из модулей расходится, то ряд исследуется на условную сходимость. Если он знакочередующийся, то применяют признак Лейбница, если произвольный, то признак Абеля или Дирихле.

ВОПРОСЫ К ЭКЗАМЕНУ.

1.Понятие абсолютной и условной сходимости. Теорема о сходимости абсолютно сходящегося ряда. Пример достаточного признака абсолютной сходимости.

2.Знакочередующиеся ряды. Признак Лейбница.

3.Знаконеопределенные ряды. Преобразование Абеля. Признак Абеля сходимости ряда.

4. Признак Дирихле сходимости числового ряда. Примеры.

Соседние файлы в папке Лекции

#
17.05.2024567.13 Кб0F-03-Lektsia_1.pdf
#
17.05.20246.66 Mб0Metodichka_Grishina (1).pdf
#
17.05.2024353.18 Кб0VTA_lektsia_11.pdf
#
17.05.2024232.02 Кб0VTA_lektsia_12.pdf
#
17.05.2024382.65 Кб0VTA_Lektsia_13.pdf
#
17.05.2024302.83 Кб0VTA_lektsia_14.pdf
#
17.05.2024576.23 Кб0VTA_lektsia_2.pdf
#
17.05.2024450.44 Кб0VTA_lektsia_5.pdf
#
17.05.2024443.26 Кб0VTA_lektsia_7.pdf