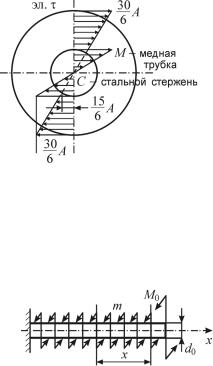
Рис. 6.29
|
|
|
Вариант |
|
2. |
Вместе контакта при |
|
ρ |
= |
d |
, |
ρ |
|
= |
d |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τс |
|
τм |
|
|
с |
|
2 |
|
|
м |
2 |
|
|
γ |
с |
= γ |
м |
= |
= |
, откуда в месте контакта τ |
с |
= 2τ |
м |
, что и показа- |
|
G |
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
м |
|
|
|
|
|
|
|
|
|
|
|
|
но на эпюре τ (рис. 6.29).
Рис. 6.30
6.6. Запишем условие прочности для любого поперечного сечения, лежащего на расстоянии x от правового торца (рис. 6.30):
|
|
τxt(max) = |
M x |
|
≤[τ] , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Wp (x) |
|
|
|
|
|
|
|
|
тогда |
M x =Wp (x)[τ] , |
M0 =Wp (0)[τ] , |
|
|
|
|
|
|
|
где Wp (x) = |
πd3 (x) |
≈ 0, 2d3 (x) , Wp (0) ≈ 0, 2d03 , |
|
|
|
|
|
16 |
|
|
M0 |
|
|
m |
|
|
|
mx |
|
M x = M0 + mx , откуда d3 (x) = |
|
+ |
x = d03 |
+ |
. |
0, 2[τ] |
0,2[τ] |
|
|
|
|
|
|
|
|
0, 2[τ] |
281
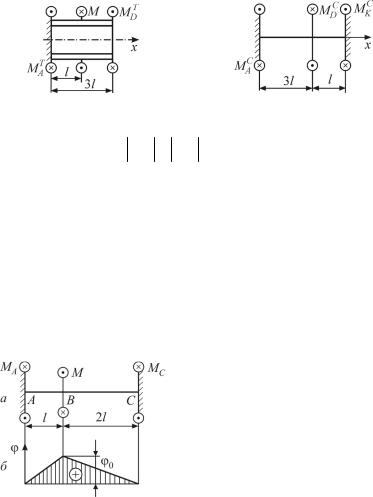
6.7. Представим расчетную схему для трубки (рис. 6.31) и для стержня (рис. 6.32). Уравнение равновесия для трубки:
∑mx = 0 , −M Aт + M − M Dт |
= 0 , |
(1) |
а для стержня: |
|
|
∑mx = 0 , −M Ac + M Dc − M Kc |
= 0 . |
(2) |
С учетом того, что M Dт = M Dc , задача 2 раза статически неопределимая (имеем два уравнения и четыре неизвестных).
Дополнительные уравнения будут: |
|
ϕтD = ϕcD ; |
(3) |
ϕcK = ϕcK (M Dc ) + ϕcK (M Kc ) = 0 . |
(4) |
Уравнения (1) – (4) дают возможность определить все моменты, а
|
|
|
|
|
|
|
|
|
|
следовательно, и крутящие моменты M x , найти M xт(max) , |
M xc(max) , |
|
(τmax )c |
|
|
M c |
W т |
|
|
|
после чего определить |
= |
|
x(max) p |
. |
|
|
|
(τmax )т |
|
|
|
|
|
|
Wpc M xт(max) |
|
|
|
|
|
|
|
|
6.8. Покажем |
направление |
|
|
|
|
моментов в |
|
заделке |
A, С |
|
|
|
|
(рис. 6.33, а), |
откуда |
следует, |
что на участке AB |
M x > 0 , на |
участке BC – M x < 0 . |
|
|
Построим эпюру углов за- |
кручивания (рис. 6.33, б). |
D |
Согласно (6.7) γ |
AB |
l = ϕ |
|
|
0 2 |
Рис. 6.33
и γBC 2l = ϕ0 D2 – для сечения B; тогда γAB = ϕ0 2Dl , γBC = ϕ0 4Dl ,
τmaxAB = γABG = 2 !
τmaxBC γBCG
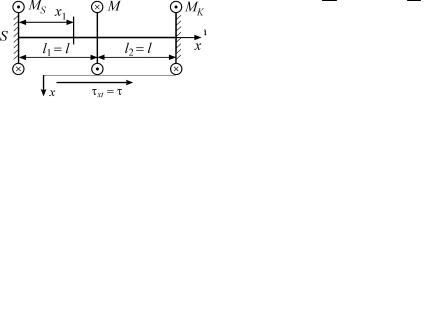
6.9. Согласно формулам (6.4) и (6.5) и указания I на гранях элемента будут действовать напряжения, как показано на рис. 6.34,
|
τxt = τ = |
σn |
направлено против часовой стрелки, следовательно, |
|
sin 2α |
|
|
|
|
на участке l1 |
M x < 0 , тогда и момент в левой заделке должен |
быть направлен против часовой стрелки (рис. 6.35), чем и определяется направление моментов M и M K .
Рис. 6.34 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 6.35 |
|
Так как |
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
M x ρ( A) |
|
Ms |
|
|
|
|
|
|
σ |
|
|
|
|
|
|
2 |
|
|
|
|
|
n |
|
|
|
τxt ( A) = |
1 |
= |
|
|
|
|
|
|
= |
|
|
|
найдем M, |
J p |
π(2d)4 |
|
− |
πd 4 |
|
sin 2α |
|
|
|
|
|
|
|
|
|
|
|
32 |
|
32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Связь между Ms и M установим из условия, что |
|
|
|
ϕs |
= |
M sl |
+ |
|
Msl |
− |
|
Ml |
= 0 , |
|
(*) |
|
|
|
|
GJ ′p |
|
|
|
|
GJ p |
GJ ′p |
|
|
|
|
|
где J p – полярный момент инерции на участке l1 ; J ′p |
– полярный |
момент инерции на участке l2 .
Из (*) найдем значение M.
6.10. Вариант 1. 1. После удаления моментов в трубке (т) и валике (в) возникнут крутящие моменты
так как система сохранит равновесие!
2. После приваривания трубки и удаления моментов M, сумма углов закручивания трубки и валика будет равна углу закручивания трубки от момента M, т.е.
|
|
|
|
Ml |
|
= |
|
Mвl |
+ |
M тl |
|
. |
(2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
GJ вp |
GJ вp |
|
|
GJ pт |
|
|
|
3. Из (1) и (2) получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Mт |
= Mв = |
|
M |
|
, |
|
|
|
|
1 + |
|
J вp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
πd3 |
|
πD3δ |
|
|
|
|
|
|
J pт |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
т |
. |
Определим максимальное касательное |
где J p = |
, |
J p = |
4 |
|
|
32 |
|
|
|
|
|
|
M xρmax |
|
|
|
|
|
напряжение по формуле τmax = |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J p |
|
|
|
|
|
|
|
Вариант 2. Потенциальная энергия стержня (валика – в) с вы-
|
|
M 2l |
|
|
ступами при приложении момента M0 до приварки: U = |
0 |
. |
|
2GJ вp |
|
|
|
Потенциальная энергия системы после приварки трубки (т) (при этом M0 уменьшается на М), а Mв = M т = M , будет равна:
|
|
Uсистемы = |
|
(M |
0 |
− M )2 l |
+ |
|
M 2l |
|
. |
|
|
|
|
|
|
|
|
|
2GJ вp |
|
|
|
2GJ pт |
|
|
|
На основании теоремы |
|
о |
минимуме |
потенциальной энергии |
(теорема о наименьшей работе): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dU |
системы |
|
|
d |
|
|
(M 2 |
− 2M |
0 |
M + M 2 )l |
|
|
M 2l |
|
|
|
= |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
+ |
|
|
= |
|
|
dM |
|
dM |
|
|
|
|
|
|
|
2GJ в |
|
|
|
|
|
|
2GJ т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
p |
|
|
|
|
|
= − |
M0l |
+ |
Ml |
+ |
Ml |
|
= 0 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
GJ pт |
|
|
|
|
|
|
|
|
|
|
|
|
|
GJ вp |
|
|
|
GJ вp |
|
|
|
|
|
|
|
|
|
откуда M = Mв = M т |
= |
|
M0 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
+ |
|
вp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J pт |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
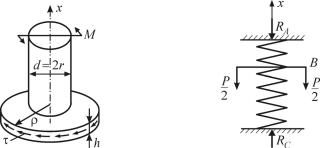
6.11. 1. Цилиндрической поверхностью с осью х сделаем сечение в плите (радиус цилиндра ρ!). В сечении будут действовать только τ (рис. 6.36). Уравнение равновесия будет:
|
∑mx = 0 ; −M + τ 2πρ h ρ = 0 τ = |
|
|
M |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2πρ2 h |
2. |
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ2 |
|
∞ |
|
M 2 |
|
|
|
|
M 2 |
|
U = ∫ |
|
dv = ∫ |
|
|
2πρ h dρ = |
|
. |
|
|
(2πρ2h)2 2G |
|
|
v 2G |
|
r |
|
|
|
|
4πhr2G |
3. |
Работа |
|
|
M ϕ |
|
|
M |
|
|
|
|
|
|
A = |
=U , откуда ϕ = |
. |
|
|
2 |
|
|
|
|
|
|
|
|
2πhr2G |
|
|
|
Рис. 6.36 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 6.37 |
|
6.12. 1. Расчетная схема представлена на рис. 6.37. |
|
2. Тогда уравнение равновесия будет: |
|
|
|
|
|
|
|
|
|
|
|
∑x = 0 , −RA + P − Rc = 0 , |
|
|
(1) |
т.е. задача один раз статически неопределимая. |
|
|
|
3. Дополнительное уравнение имеет вид |
|
|
|
|
λ |
AB |
|
= |
|
λ |
BC |
|
= |
8D3 n |
R |
A |
= |
|
8D3 2n |
R , |
(2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Gd 4 |
|
|
|
|
Gd 4 |
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и с учетом (1) определим RA и RB . |
|
|
R(max) D 8 |
|
|
4. По формуле (6.18) найдем τmax = |
|
, а смещение се- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π d3 |
|
|
|
чения B будет λ |
B |
= λAB |
R |
A |
, или λ |
B |
= λBC R . |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
C |
|
|
|
Рис. 6.38
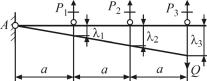
6.13. 1. Из силовой и деформационной схемы (рис. 6.38) будем иметь:
∑mA = 0 , Q 3a − P3 3a − P2 2a − P1 a = 0 , |
(1) |
|
|
λ1 |
= |
λ2 |
= |
λ3 |
|
|
|
|
|
|
3a |
|
|
|
a |
|
|
2a |
|
|
|
|
|
|
|
|
8D3 |
n |
|
|
|
|
|
или, подставляя значения λ |
i |
= |
|
|
|
i |
|
|
P , получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
Gdi4 |
i |
|
|
|
|
|
|
|
|
|
P3 |
|
|
81 |
P1 |
= |
96 |
P2 |
=125 |
. |
(2) |
d 4 |
|
|
|
|
|
|
|
d |
4 |
|
|
|
d 4 |
|
1 |
|
|
|
|
2 |
|
3 |
|
|
2. По условию равнопрочности τmax(1) = τmax(2) = τmax(3) =[τ] , где
τmax(i) = |
Pi Di 8 |
, будем иметь |
|
|
|
|
π di3 |
|
P3 |
|
|
|
|
P1 |
|
P2 |
|
|
|
|
|
3 |
= 4 |
= 5 |
. |
(3) |
|
|
d3 |
d3 |
|
|
|
|
|
|
d3 |
|
|
|
1 |
2 |
3 |
|
|
3. Возведем (2) в третью, а (3) в четвертую степень и разделим одно на другое (таким образом, избавимся от di !) и получим
|
|
|
|
(5) |
|
|
|
|
|
(3) |
4 |
P = |
(4)4 |
P = |
(5)4 |
P , |
|
|
|
|
(81)3 |
1 |
(96)3 |
2 |
(125)3 |
2 |
|
|
|
(4)
т.е. получим два дополнительных уравнения (4) и (5).
4. Решая совместно (1), (4), (5), найдем P1 , P2 , P3 . Из условия
|
прочности для каждой пружины τmax = |
Pi Di 8 |
≤[τ] найдем di ! |
|
πdi3 |
|
|
|
|
286 |
|
|
СПИСОК ЛИТЕРАТУРЫ
(жирным шрифтом выделена рекомендуемая литература)
1.Аксельрод Э.Р., Бернацкий С.А., Возлинский В.И. и др. Методические указания к решению задач по сопротивлению материалов для подготовки к студенческим олимпиадам. – Ч. 1. – М.:
МАДИ, 1983. – 64 с.
2.Ахметзянов М.Х., Геронимус В.Б., Грес П.В. и др. Сборник олимпиадных задач по сопротивлению материалов. – Новосибирск:
СГАПС, 1995.
3.Беляев Н.М. Сборник задач по сопротивлению материа-
лов. – М.: ГИТТЛ, 1956. – 347 с.
4.Беляев Н.М. Сопротивление материалов. – М.: Наука, 1976. – 608 с.
5.Бидерман Т.В., Боровникова Н.Н. Методические указания к
решению задач Всероссийской олимпиады по сопротивлению материалов. – М.: Изд-во МГТУ им. Н.Э. Баумана, 1997. – 12 с.
6.Варданян Г.С., Андреев В.И., Атаров Н.М., Горшков А.А. Сопротивление материалов с основами теории упругости и пластичности / Под ред. Г.С. Варданяна. – М.: Ассоциация строительных вузов, 1995. – 568 с.
7.Всероссийская студенческая олимпиада по сопротивлению ма-
териалов в НГТУ г. Новочеркасска / Сост. Р.К. Вафин, 1997. – 1 с.
8.Исаченко В.В. Статически неопределимые задачи при растя- жении-сжатии. – М.: МИФИ, 2003. – 68 с.
9.Исаченко В.В. Учебно-методическое пособие для решения задач студенческих олимпиад по сопротивлению материалов. –
Ч. 1 – 4. – М.: МИФИ. Ч. 1. 1998; Ч. 2. 2000; Ч. 3. 2000; Ч. 4. 2001.
10.Исаченко В.В., Мартиросов М.И., Щербаков В.И. Учебное пособие по решению конкурсных задач по сопротивлению материалов / Под ред. В.В. Исаченко. – Изд. 2-е, испр. и доп. –
М.: МИФИ, 2006. – 248 с.
11.Итоги и задачи внутривузовских, областных и региональных олимпиад по сопротивлению материалов. Методическая разработка / Сост. Ю.В. Глявин, Н.А. Ильичев. – Горький: ГПИ, 1990. – 44 с.
287
12.Клюева Г.П., Сосновский Е.В. Методические указания к решению задач Всероссийской олимпиады по сопротивлению материалов/ Подред. Д.Н. Спицыной. – М.: МГТУим. Н.Э. Баумана, 1992.
13.Нестандартные задачи по сопротивлению материалов. Учебное пособие. – В 2-х ч. – Ч. 1 / Сост. Ю.В. Глявин, Н.А. Ильичев и др. – Самара: НПЦ «Авиатор», 1995. – 170 с.
14.Нестандартные задачи по сопротивлению материалов. Учебное пособие. – В 2-х ч. – Ч. 2 / Сост. Ю.В. Глявин, Н.А. Ильичев и др. – Самара: НПЦ «Авиатор», 1996. – 60 с.
15.Окопный Ю.А., Радин В.П., Хроматов В.Р и др. Механика материалов и конструкций. Справочные материалы / Под ред. В.П. Чиркова. – М.: изд-во МЭИ, 2005. – 124 с.
16.Олимпиады по сопротивлению материалов. Сборник зада-
ний / Сост. Д.Ф. Бибиков. – Йошкар-Ола: МарПИ, 1987. – 40 с.
17.Писаренко Г.С., Яковлев А.П., Матвеев В.В. Справочник по сопротивлениюматериалов. – Киев: НауковаДумка, 1988. – 725 с.
18.Пособие к решению задач по сопротивлению материалу. – М.: Высшая школа, 1985.
19.Предметные олимпиады. Организация и задачи / Сост. Ю.В. Глявин, Н.А. Ильичев и др. – Горький: ГПИ, 1986. – 104 с.
20.Феодосьев В.И. Избранные задачи и вопросы по сопротивлению материалов. – М.: Наука, 1973.
21.Феодосьев В.И. Сопротивление материалов. – М.: МГТУ им. Н.Э. Баумана, 2000. – 592 с.
22.Щербаков В.И., Мартиросов М.И. Московские городские
олимпиады по сопротивлению материалов (1992 – 1998 гг.). Задачи, решения и итоги. – М.: МГТУ «МАМИ», МГАИ (ТУ), 1998.
______________________
Редактор и технический редактор М.В. Макарова
Подписано в печать 23.03.2010. Формат 60х84 1/16
Уч.-изд.л. 18,0. Печ.л. 18,0. Тираж 500 экз.
Изд. № 098-1. Заказ № 114
Национальный исследовательский ядерный университет «МИФИ». Типография НИЯУ МИФИ.
115409, Москва, Каширское ш., 31