Пример интегрирования уравнения упругой линии балки
M
O |
|
|
|
x |
|
|
A |
||
|
|
|
||
|
L |
|
MZ (x) = M = const |
|
|
||||
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Граничные условия – угол поворота и прогиб в заделки равны нулю, т.е.
θ(0) = 0 и y(0) = 0.
Это дает нулевые постоянные интегрирования
c = 0 и d =0.
M x |
M L |
x EIz ; |
x L EIz ; |
M x2 |
M L2 |
y x 2EIz ; |
y x L 2EIz . |
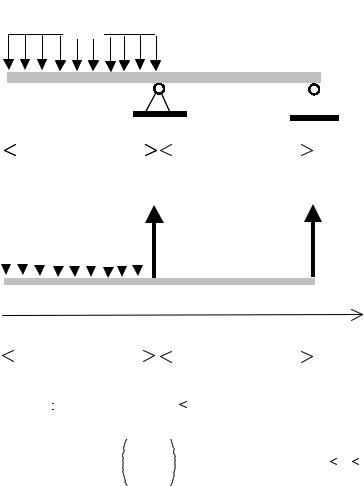
Пример численного интегрирования уравнения упругой линии балки
q
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
a = 1 m |
; |
q = |
|
1 0 к Н / м . |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
2 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
1 |
|
3 a |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
|||||
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
R 2 |
|
|
|
qa |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||||||||||||||
M z ( x ) |
|
|
|
|
q x |
|
x |
|
|
|
if |
0 |
|
|
|
|
|
x a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
q a |
|
x |
|
|
|
|
a |
|
|
|
|
|
|
|
R |
1 |
( x |
|
|
a ) |
if |
a |
|
x |
|
2 a |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
0 |
|
kN |
|
|
m |
|
|
|
otherwise |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Пример численного интегрирования уравнения упругой линии балки (продолжение 1)
E |
|
2 105 MPa |
I |
z |
|
100 cm4 |
|
|
|||||
|
|
Given
a |
x |
|
|
|
|
M z(x) |
dxdx C1 a |
C2 0 m |
|
|
E I |
|||
0 m |
z |
|
|
|
0 m |
|
|
||
2 a |
x |
|
|
|
|
M z(x) |
dxdx C1 2 a |
C2 0 m |
|
|
E I |
|||
0 m |
z |
|
|
|
0 m |
|
|
||
C1 |
Find(C1 C2) |
C1 0.017 |
C2 14.577 mm |
|
C2 |
||||
|
|
|
Зависимость угла поворота сечения балки от координаты сечения
Угол поворота, градусы
|
x |
|
|
(x) |
M z(x) |
dx C1 |
|
E I |
|||
|
|
||
|
z |
|
|
|
0 |
|
1Углы поворота сечений балки
(x) 0.5 
deg
0 |
|
|
|
|
0.5 0 |
0.5 |
1 |
1.5 |
2 |
x
m Координата сечения, м
Зависимость прогиба балки от координаты сечения
Прогиб, мм
y(x)
mm
10
|
x |
y(x) |
(x) dx C2 |
|
0 |
|
Прогибы балки |
0 |
|
|
|
|
|
10 |
|
|
|
|
|
20 |
0 |
0.5 |
1 |
1.5 |
2 |
|
|
|
x |
|
|
m Координата сечений, м