
Курс лекций по дисциплине МЖиГ
.pdf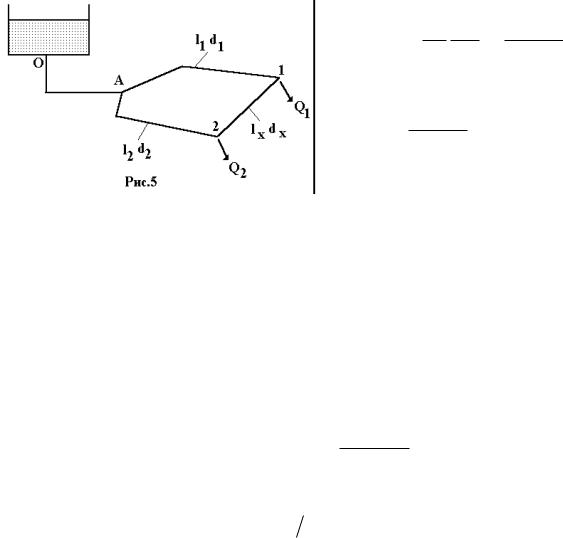
56
|
|
|
|
|
|
|
dx V |
2 |
|
8Q |
2 |
|
|||||
|
|
|
|
|
|
|
|
|
x |
|
|||||||
dh |
w |
|
|
|
|
x |
|
|
|
|
dx . |
||||||
d |
2g |
|
2 |
|
5 |
||||||||||||
|
|
|
|
|
|
d |
g |
||||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
Отсюда |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
l |
8Q |
2 |
|
|
|
|
|
|
|
|
||
dh |
|
|
|
|
x |
|
dx . |
|
|
|
|
||||||
w |
|
|
|
|
|
|
|
|
|||||||||
|
2 |
|
5 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
0 |
d |
g |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(10)
Если течение происходит в квадратичной зоне сопротивления, то коэффициент трения
0.11 kэ 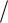 d 0.25
d 0.25
не зависит от х и интегрирование в формуле (10) проводится элементарно:
|
|
|
|
8 l |
|
|
|
|
|
|
|
|
Qс2 |
бр |
|
|
||
h |
w |
|
|
|
|
|
|
Q2 |
Q |
cбр |
Q |
0 |
|
|
|
. |
(11) |
|
|
2 |
|
5 |
|
|
|
||||||||||||
|
|
|
d |
|
|
0 |
|
|
|
3 |
|
|
|
|||||
|
|
|
|
|
g |
|
|
|
|
|
|
|
|
|
||||
В частном случае, когда на участке сбрасывается весь расход (QСБР= QO), из уравнения (11) получим
|
|
|
|
|
|
2 |
|
|
|
|
|
|
8 lQ |
|
|
|
|||
h |
w |
|
|
|
|
0 |
. |
(12) |
|
3 |
2 |
|
5 |
|
|||||
|
|
d |
g |
|
|
||||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||
Если движение происходит в неквадратичной зоне сопротивления
|
|
d |
0.11 k |
э |
|
|
|
68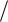 Re
Re
0.25
,
а так как число Рейнольдса зависит от QX, интегрирование уравнения (10) значительно усложняется. В этом случае все равно пользуются формулами (11) и (12), находя потери напора методом последовательных приближений, полагая сначала (в нулевом приближении) независящим от Re (квадратичная область), а затем делая поправку.
Кольцевой трубопровод показан на рис.5. Основной расчетной задачей является определение напора Н в условиях, когда заданы значения расхода в точках отбора (так называемые узловые расходы Q1, Q2, ... , Qn), расположение трубопровода, длины отдельных участков и диаметры всех труб.
В нашем случае трубопровод имеет два узловых расхода Q1, Q2. Определение потерь затруднено тем, что неизвестны ни расход, ни направление потока на замыкающем участке 1-2, в связи с чем неизвестны расходы на других участках трубопровода. Если, например, течение происходит от узла 1 к узлу 2, то расход трубопровода на участке А-1 будет QA 1 Q1 Qx ,
где QX - расход на участке 1-2, а если течение происходит от узла 2 к узлу 1, то на том же участке расход равен QA 1 Q1 Qx .
57
Поэтому нужно предварительно ре-шить вопрос о замыкающем участке трубопровода и найти точку схода (узел, к которому вода примыкает с двух сторон).
Потери напора от магистральной узловой т.А до точки схода одинаковы по обоим направлениям кольца.
Точка схода определяется следующим образом. Предположим, что точкой схода является т.2. Тогда
hw hw hw . |
||
А 2 |
А 1 |
1 2 |
Следовательно, |
|
|
hw hw . |
||
А 2 |
|
А 1 |
Пренебрегая местными потерями и учитывая, нии QA 2 Q2 Qx и QA 1 Q1 Qx
что в принятом предположе- , из последнего неравенства
получим
|
l |
|
|
Q |
|
Q |
|
|
|
2 |
||
|
2 |
2 |
x |
|
||||||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
d |
|
|
2gS |
2 |
|
|
|
|
|||
|
2 |
|
|
|
|
|
||||||
|
|
2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||
И тем более, опуская QX |
|
|
|
|
|
|
|
|
||||
|
|
|
|
2 |
l |
2 |
Q |
2 |
2 |
|||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
d2 |
2gS2 |
|||||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
l |
|
|
1 |
|
1 |
d |
|
|
||
|
1 |
|
1 |
l1 |
|
d1 |
||
|
Q |
|
Q |
|
|
|
|
|
|
|
|
2 |
|
1 |
|
|
x |
. |
|
|
|
2 |
|
|
|
2gS |
|
|
||
|
1 |
|
|
||
|
|
|
|
|
|
Q1 2 .
2gS12
Если расчет показывает, что знак неравенства нужно поменять на обратный, это значит, что точкой схода является 1.
После того, как решен вопрос о точке схода, искомый начальный напор определяется путем вычисления в каком-нибудь одном направлении потерь напора до точки схода от начального сечения трубопровода, напри-
мер:
H z |
2 |
|
|
|
hw O A 2
.
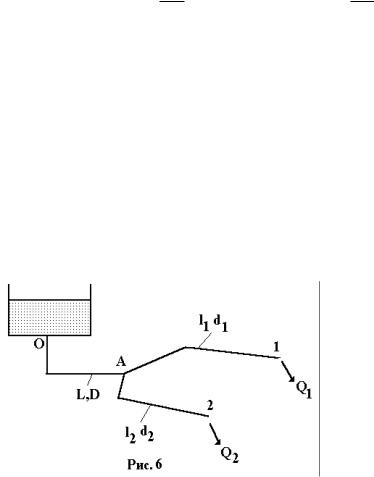
Простая разветвленная сеть
представлена на рис.6.
Основными задачами можно считать: определение напора при заданных концевых расходах Q1 и Q2 при заданном напоре в начальном сечении или определение напора при заданных концевых расходах
Q1 и Q2.
В качестве примера рассмотрим первую задачу. Составим уравнение Бернулли для потока вдоль линии О-А-1, а затем - вдоль линии О-А-2. В пер-
вом случае
H0 z1 hw hw ;
O A A 1

|
58 |
во втором |
hw |
H0 z2 |
|
|
O A |
hw A 2
.
Потери напора на магистральной линии
|
8 Q |
1 |
Q |
2 |
|
2 |
|
|
|
L |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
hw |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g 2D 4 |
|
|
|
|
|
|
|
|
|||||||||||
О А |
|
|
|
|
|
|
|
|
|
D |
|
||||||||||
Аналогично |
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
||||
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||
hw |
|
8 Q |
1 |
|
|
|
|
|
|
1 |
|
||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|||||||||||
|
g |
|
|
d |
|
|
|
d |
|
||||||||||||
А 1 |
|
|
|
2 |
4 |
|
|
|
|
1 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
l |
|
|
|||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||
hw |
|
8 Q |
2 |
|
|
|
|
|
|
|
2 |
|
|||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|||||||||||
|
g |
|
|
d |
|
|
|
d |
|
||||||||||||
A 2 |
|
|
|
2 |
|
4 |
|
|
|
|
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||
B Q1
B |
Q |
1 |
|
B |
Q |
2 |
|
Q 2 2 .
1 |
|
2 |
, |
|
|
|
|
2 |
|
2 |
. |
|
|
|
H
Таким образом, исходные уравнения запишутся в виде:
|
z |
|
B Q |
Q |
2 |
|
2 |
, H |
|
z |
|
B Q |
|
Q |
|
|
2 |
0 |
1 |
|
B Q |
0 |
2 |
1 |
2 |
|
|||||||||
|
1 |
2 |
|
1 |
1 |
|
|
|
|
|
|
||||||
B |
Q |
2 |
|
2 2
.
Эти уравнения позволяют найти по наоборот, по известному напору - расходы. противления во втором случае используют ближений.
известному расходу напор и, В неквадратичной области сометод последовательных при-
61
ЛЕКЦИЯ 13
ПОСТАНОВКА ЗАДАЧ МЕХАНИКИ ЖИДКОСТИ И ГАЗА
Зачастую в инженерной практике возникают задачи, работа над которыми требует знания свойств и характеристик течений жидкостей или газов в том или ином устройстве, т. е. умения решать гидродинамические задачи. В ряде случаев можно воспользоваться справочниками. Но и здесь необходимо хорошо представлять, какими именно данными следует воспользоваться, как провести оценки, как выбрать оптимальные технологические параметры. Для этого нужна соответствующая теоретическая подготовка. Если же инженер - личность, причем личность творческая, без самостоятельного решения задач механики жидкости и газа ему не обойтись. Обусловлено это тем, что настоящий инженер не просто шагает протоптанными тропами, но и создает новые (или усовершенствует известные) аппараты и устройства. Такая деятельность всегда включает предварительный теоретический анализ идей, лежащих в основе предлагаемой разработки. Этот анализ, в свою очередь, базируется на исследовании течения жидкости или газа, т.е. на решении гидродинамической задачи.
Решить задачу гидродинамики, в общем случае, значит найти поле скоростей и давлений, реализующееся при течении жидкости или газа. Но для того, чтобы решить задачу, ее необходимо сначала поставить, т.е. выписать уравнения, описывающие рассматриваемое течение и условия, которым оно должно удовлетворять.
13.1. Уравнение неразрывности
Начнем вывод основных гидродинамических уравнений с вывода уравнения, выражающего собой закон сохранения вещества в гидродинамике.
Рассмотрим некоторый объем V0 пространства. Количество (масса)
жидкости в этом объеме |
|
|
, |
|
m |
dV |
|||
|
|
где - плотность жидкости, а интегрирование производится по объему V0.
Через элемент ds поверхности, ограничивающей рассматриваемый
объем, в единицу времени протекает следующая масса жидкости: v d s ;
|
|
v |
- скорость, вектор ds по абсолютной величине равен площади элемента |
|
|
поверхности и направлен по нормали к ней. Условимся направлять ds по

62
внешней нормали. Тогда
v d s
положительно, если жидкость вытекает из
объема, и отрицательно, если втекает в него. Следовательно, полное коли-
|
|
|
|
чество жидкости, вытекающей из объема, есть |
v d s |
, где интегрирование |
|
|
|
||
проводится по всей замкнутой поверхности, охватывающей рассматриваемый объем.
С другой стороны, уменьшение массы жидкости в объеме V0 можно
написать в виде |
|
|
|
|
|
|
|
dV . |
|
t |
||||
|
||||
|
|
|
Приравнивая оба выражения, получаем
|
|
t |
dV v d s |
|
.
Интеграл по поверхности преобразуем в интеграл по объему (формула Остроградского Гаусса)
|
|
|
|
|
|
v d s |
|
|
|
||
|
|
div |
v dV |
||
|
|
|
|
|
|
|
|
|
|
|
v dV |
|
|
|
|
|
|
.
Таким образом,
|
|
|
|
|
|
|
div |
v dV |
|
|
t |
|
|
|
|
|
|
||
|
0
.
Поскольку это равенство должно иметь место для любого объема, то должно быть равным нулю подынтегральное выражение, т.е.
|
|
|
|
|
div |
v |
|
t |
|
|
|
|
|
||
|
0
.
(1)
Это
div
Или
- так называемое уравнение неразрывности. Раскрыв выражение |
||
|
|
|
v |
|
, можно записать (1) в виде |
|
||
|
|
|
|
|
|
|
|
||
t |
v grad div v |
0. |
(2) |
|||
|
d |
|
|
|
|
|
|
div v |
0 . |
|
(3) |
||
|
|
|
||||
|
dt |
|
|
|
||
13.2. Уравнения движения (уравнения Навье-Стокса)
Уравнения Навье-Стокса являются аналогом второго закона Ньютона в механике твердого тела и выражают собой фундаментальный закон изменения импульса. Строгий их вывод много сложнее вывода уравнения нераз-

63
рывности, поэтому уравнения движения приводятся без доказательства, за которым можно обратиться к многочисленным учебным пособиям.
В декартовой системе координат уравнения движения имеют вид
|
|
|
du |
u |
|
|
|
u |
|
|
|
u |
|
|
u |
|
|
xx |
|
|
yx |
|||||||||
|
|
|
|
|
|
|
u |
|
|
v |
|
|
w |
|
fx |
|
|
|
|
|
|
|||||||||
|
dt |
t |
x |
y |
|
|
x |
|
y |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
||||||||||||||
|
|
dv |
|
v |
u |
v |
v |
v |
w |
v |
fy |
xy |
|
yy |
|
|||||||||||||||
|
dt |
|
|
x |
y |
|
|
|
x |
|
y |
|||||||||||||||||||
|
|
|
t |
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|||||||||||||
|
dw |
|
|
w |
|
|
|
w |
|
|
w |
|
|
w |
|
|
xz |
|
|
yz |
|
|||||||||
|
|
|
|
u |
|
|
|
v |
|
|
|
w |
|
|
fz |
|
|
|
|
|
|
|||||||||
dt |
x |
y |
|
|
x |
|
|
y |
||||||||||||||||||||||
|
|
|
t |
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|||||||||||||
zyz
zzz
zx z
,
,
(4)
(5)
(6)
где (u,v,w) - проекции скорости на оси декартовой системы координат (x,y,z)
соответственно, fx, fy, fz - составляющие массовых сил, |
|
ij |
- компоненты тен- |
|
|
|
зора напряжений, физически каждая из которых означает силу трения на единице поверхности, действующую на элементарную площадку, перпендикулярную i-ой оси, в направлении оси j.
Левая часть уравнений (4)-(6), как ясно из самой записи, - это ускорение жидкой частицы, а в правой стоят действующие силы: массовые и поверхностные соответственно.
В декартовой системе координат компоненты тензора касательных напряжений
|
|
p 2 |
u |
, |
|
|
|
p 2 |
v |
, |
|
|
p 2 |
w |
, |
|||
xx |
x |
yy |
y |
zz |
z |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
u |
|
v |
|
|
|
|
u |
|
w |
|
|
|||
|
|
xy yx |
y |
|
, xz zx |
|
z |
, |
|
|
||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
x |
|
|
||||
zy |
|
w |
|
v |
yz |
y |
|
|
|
|
|
|
z |
В общем случае, как говорилось во введении, вязкость является функцией температуры, поэтому для полноты постановки нужно выписывать уравнение для температуры, представляющей собой уравнение сохранения энергии. Однако нами в настоящем курсе будут рассматриваться изотермические течения. При этом вязкость жидкости является постоянной величиной. Далее, в рассматриваемых течениях (течения в трубах, в пограничных слоях и т.д.), перепады давления по сравнению с его абсолютной величиной незначительны. Поэтому, опять же в связи со сказанным во введении, при изучении движений газа можно считать его несжимаемой средой, т.к. .
Итак, в последующем (если не оговорено обратное) принимается, что и вязкость, и плотность - величины постоянные как для жидкости, так и для газа. Говоря “жидкость”, будет подразумеваться и газ, и наоборот.

64
При постоянной плотности уравнение
наиболее простой вид:
div v 0 .
Или, в декартовых координатах, |
|
|
|
|
|
u |
|
v |
|
w |
|
x |
y |
z |
|||
|
|
неразрывности (1) принимает
0. |
(7) |
Уравнения движения при постоянных плотности и вязкости (как это следует при подстановке выражений для в (4-6) и несложных преобразований с привлечением уравнения (7)), имеют вид:
u |
|
|
|
u |
|
|
|
u |
|
|
u |
fx |
p |
|
|||||
|
|
|
u |
x |
|
v |
y |
w |
|
|
x |
|
|||||||
t |
|
|
|
|
|
|
|
|
|
z |
|
|
|||||||
|
v |
|
|
|
v |
|
|
|
v |
|
|
v |
fy |
p |
|
||||
|
t |
|
u |
x |
v |
y |
|
w |
|
y |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
||||||
w |
|
|
|
w |
|
|
w |
|
|
w |
fz |
p |
|
||||||
|
|
u |
x |
v |
|
y |
w |
|
|
z |
|
||||||||
t |
|
|
|
|
|
|
|
|
|
z |
|
|
|||||||
|
2 |
u |
|
|
2 |
u |
|
|
2 |
u |
|
|
|
|
|
|
|||||||
|
|
2 |
|
|
2 |
|
|
2 |
|
||
x |
|
y |
|
z |
|
||||||
v |
|
v |
|
|
|||||||
|
2 |
|
|
2 |
|
|
2 |
v |
|||
|
|
|
|
|
|
|
|
|
|||
|
|
2 |
|
|
|
2 |
|
|
|
2 |
|
x |
|
y |
|
z |
|
||||||
|
|
|
|
|
|||||||
|
2 |
w |
|
|
2 |
w |
|
|
2 |
w |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
2 |
|
x |
|
y |
|
z |
|
|||||||||
|
|
|
|
|
||||||||||
(8)
(9)
. (10)
Итак, нами построена система уравнений (7)-(10), описывающая движение жидкости (газа) с постоянными вязкостью и плотностью в декартовой системе координат.
Первое слагаемое в правой части уравнений (8-10) называют обычно
объемными (или массовыми) силами, вторые - силами давления, третьи - вяз-
кими; вторые и третьи вместе получили название поверхностных сил.
13.3. Граничные и начальные условия
Решение выписанной системы уравнений (7-10) неединственно: она описывает огромное множество самых разнообразных движений жидкости. Для получения решения в каком-либо конкретном случае нужно поставить граничные условия, которые должны выполняться на ограничивающих жидкость поверхностях.
Если жидкость ограничена непроницаемой твердой стенкой, на ней ставится так называемое условие прилипания: частицы жидкости, граничащие со стенкой, “прилипают” к ней, поэтому скорость их равна скорости стенки. Например, в случае неподвижной твердой поверхности скорость частиц жидкости на границе с ней должны обращаться в нуль.
Если жидкость контактирует с другой жидкостью или газом, то поверхность контакта называют поверхностью раздела. На ней ставятся условия равенства скоростей и компонент тензора напряжений в соприкасающихся средах. Суть первого условия - то же прилипание, только уже не к
65
твердой стенке, а к частицам другой жидкости; второе - не что иное, как третий закон Ньютона: с какой силой одна среда воздействует на другую, таким же будет и противодействие. Но так как силы, действующие на границе раздела, можно представить в виде суммы нормальных (за которых отвечает давление) и касательных (касательное напряжение) составляющих, то граничные условия в этом случае сводится к равенству скоростей, давлений и касательных напряжений. Последние - не что иное, как недиагональные компоненты тензора ij, i j. В литературе можно еще встретить “компоненты
тензора напряжения трения |
”, выражения для которых получаются, если в |
|||||||
|
|
ij |
|
|
|
|
|
|
выписанных выше функциях для ij опустить слагаемые с давлением: |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
i j; |
|
|
ij |
|
|
|
- символ Кронеккера. |
||||
ij p ij ij , где |
|
|
1, |
i j. |
||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
В том случае, когда на поверхности раздела трением сред друг о друга можно пренебречь (часто это справедливо на границе контакта “жидкостьгаз”), мы имеем дело с так называемой свободной поверхностью. Точки, лежащие на ней, должны удовлетворять следующим условиям. Во-первых, давление на них равно статическому давлению в соседней фазе (например, на поверхности реки давление равно атмосферному, если течение не слишком сильное и трение воды о воздух пренебрежимо мало). Во-вторых, так как силы отсутствуют (отсюда и название - свободная поверхность), должны обращаться в нуль касательные напряжения (компоненты тензора касательных напряжений). И в-третьих, ставится кинематическое условие, суть которого в том, что частицы жидкости, находящиеся на поверхности, движутся вместе с поверхностью. Если F(t,x,y,z)=0 - уравнение свободной поверхности, то кинематическое условие имеет вид:
dF |
|
F |
|
|
|
|
|
|
|
|
|
|||
dt |
t |
v |
F 0. |
|
|
|
|
Или в декартовых координатах
F |
u |
F |
v |
F |
w |
F |
|
|
t |
x |
y |
z |
|||||
|
|
|
|
0
.
В том случае, если процесс нестационарный, должны быть поставлены начальные условия, заключающиеся в задании поля скоростей и давлений в начальный момент времени.
Наконец, если о потоке что-либо известно (например, его симметричность, перепад давлений, средняя скорость, расход, ...), при постановке задачи эта известная величина используется как дополнительное условие.
13.4. Уравнения движения в криволинейных координатах

66
Приведем для справки уравнения движения жидкости (газа) постоянной вязкости и плотности в часто используемых криволинейных координатах.
В цилиндрических координатах (r, ,z) компоненты тензора напряжений выглядят следующим образом:
|
|
|
|
W |
|
|
|
|
|
|
|
|
|
1 |
W |
|
W |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
rr |
p 2 |
|
|
r |
, |
|
|
p 2 |
|
|
|
|
|
r |
|
, |
|||||
|
r |
|
|
|
|
r |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|||||
|
|
|
|
W |
|
|
|
|
|
1 |
W |
|
|
|
W |
|
W |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
zz |
p 2 |
|
|
z |
|
, |
r |
|
r |
|
|
|
|
|
|
, |
||||||
z |
|
|
|
|
r |
|
r |
|||||||||||||||
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
||||||
|
|
W |
|
|
1 |
W |
|
|
|
W |
W |
|
|
|||||||||
|
z |
|
|
|
|
|
|
|
|
z |
, zr |
|
|
|
z |
z |
r . |
|
||||
|
|
|
|
r |
|
|
|
|||||||||||||||
|
|
z |
|
|
|
|
|
|
r |
|
|
|
||||||||||
Уравнения Навье-Стокса принимают вид:
|
W |
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W |
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
r |
|
|
|
|
|
|
|
|
W |
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W |
|
|
|
|
r |
|
|
|
|
W |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
W |
W |
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
t |
|
|
|
|
|
|
r |
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
r |
2 |
|
|
r |
2 |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 W |
|
||||||||||||||||
W |
|
|
|
r |
|
|
|
|
|
|
W W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W |
|
|
|
|
|
|
|
|
|
r |
|
||||||||||||||||||
|
|
|
|
|
|
W W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
t |
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
r |
|
|
|
r |
2 |
|
|
r |
2 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
W |
|
W |
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
причем операторы |
|
W |
|
|
|
|
и определяются формулами |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
W |
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
W |
|
|
f W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W |
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
r |
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
z |
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
f |
|
|
|
|
1 |
|
|
2 |
f |
|
|
|
|
|
|
|
2 |
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r r |
r |
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
z |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
2 |
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Уравнение неразрывности: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
rW |
|
|
|
|
|
|
1 W |
|
|
|
|
W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
В сферических координатах (r, , ) имеем для тензора напряжений: |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
W |
|
|
|
|
|
W |
|
|
|
|
|
W ctg |
|
|||||||||||||||||||
|
rr |
p 2 |
|
|
r , |
|
|
p 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
, |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r sin |
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
r |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 W |
|
|
|
|
|
W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 W |
|
|
|
|
|
|
W |
|
|
|
W |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
p 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
, |
|
r |
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
,
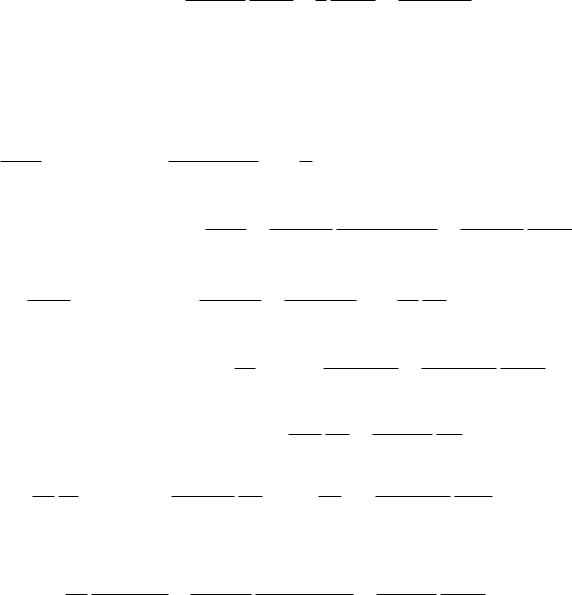
67
|
|
|
1 |
W |
|
1 |
W |
|
W ctg |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
||||||
|
r sin |
|
|
r |
|
|
r |
|
||
|
|
|
|
|||||||
|
|
|
W |
|
1 |
|
W |
W |
||
|
r |
|
|
|
|
|
r |
|
|
. |
|
|
|
|
|||||||
|
|
r |
|
r sin |
|
|
r |
|
||
|
|
|
|
|
|
|||||
Уравнения Навье-Стокса:
,
W |
|
|
r |
||
|
||
t |
|
Wt
причем
r |
|
|
r |
|
W2 W2 |
|
|
|
1 p |
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
W W |
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
r |
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
2W |
|
|
|
|
|
2 |
|
|
|
|
W sin |
|
|
|
|
|
|
|
2 |
W |
|
||||||||||
|
W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
||||||||||||||
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
r |
|
|
r |
2 |
|
|
r |
|
sin |
|
|
|
|
|
|
|
|
|
|
|
r |
|
sin |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||
|
r |
|
|
|
|
|
W W |
|
W |
2 |
ctg |
|
|
|
|
1 p |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
W W |
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|||||||||||||||||||
|
|
r |
|
|
|
|
|
|
r |
|
|
|
r |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
2 W |
|
|
|
|
|
W |
|
|
|
|
|
2 cos |
|
W |
|
|
||||||||||||
|
|
|
|
W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|||||||||||
|
|
|
|
|
|
|
|
|
r |
2 |
|
|
|
|
|
r |
|
sin |
2 |
|
|
r |
|
sin |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
||||
|
|
r |
|
|
|
|
|
|
|
f |
|
W |
|
f |
|
|
|
|
|
W |
|
f |
|
|
|
|
|
|
|
|||||||||
|
|
W f |
Wr |
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
r sin |
|
|
|
|
|
|
|
|||||||||||||||
f |
1 |
|
|
2 |
f |
|
|
|
1 |
||
|
2 |
|
r |
|
|
|
2 |
|
|||
|
r |
r |
|
|
r |
|
r |
sin |
|||
|
|
|
|
|
|
||||||
Уравнение неразрывности: |
|||||||||||
|
|
|
1 |
|
|
|
r |
|
|
1 |
|
|
|
|
|
|
|
|
r2W |
|
|
||
|
|
|
|
2 |
|
|
r |
|
r sin |
||
|
|
|
r |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
13.5. Выводы
|
|
|
f |
|
|
|
sin |
|
|||
|
|
|
|
||
|
|
|
sin W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
r |
2 |
|
r
1 |
|
sin |
2 |
|
|
1 |
|
sin |
|
2f
2
W
.
0
.
Итак, постановка задачи гидродинамики заключается в следующем:
1)выбирается система координат, в которой будет описываться течение;
2)выписать уравнение Навье-Стокса и уравнение неразрывности;
3)если возможно, на основании физических соображений или предположений о течении, упростить уравнения;
4)поставить граничные условия (и в случае нестационарных движений - начальные);
5)записать дополнительные условия, если они имеют место.
