
Курс лекций по дисциплине МЖиГ
.pdf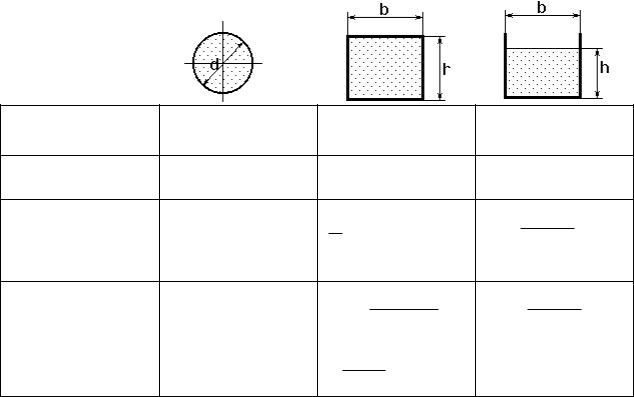
21
Для упрощения решения практических задач введено понятие средней скорости для данного сечения трубопровода:
v
Q / Q
v
,
где - площадь сечения трубопровода.
Следовательно: средняя скорость - это фиктивная скорость потока, которая считается одинаковой для всех частиц данного сечения, но подобрана так, что расход, определяемый по ее значению, равен истинному значению расхода. Изобразим эпюру изменения скорости в поперечном сечении трубы
АВ. Средняя скорость потока такова, что площадь прямоугольника ABCD равна площади эпюры истинных скоростей.
Смоченным периметром потока называется длина контура живого сечения, по которой жидкость соприкасается с ограничивающими его стенками. При напорном движении жидкости смоченный периметр совпадает с геометрическим. При безнапорном движении смоченный периметр отличается от геометрического, т.к. в него не входит линия свободной поверхности.
Смоченный периметр
геометрический
радиус
гидравлический
радиус
эквивалентный
диаметр
d |
|
|
|
r d / 2 |
|
|
|
|
d |
2 |
|
R / |
|
||
4 d |
|||
|
|||
dэ 4R d
|
2b 2h |
|||||
|
|
|
______ |
|
||
|
d |
|
|
bh |
||
R |
|
|
|
|||
|
2(b h) |
|||||
4 |
|
|
||||
|
d |
|
|
4bh |
||
|
э |
2(b h) |
||||
|
|
|
|
|||
|
|
|
|
|
||
|
|
|
2bh |
|||
|
|
b h |
||||
|
|
|
||||
2(b
h) 2h b |
||||
|
|
|
______ |
|
R |
bh |
|||
2h b |
||||
|
|
|
||
d |
|
|
4bh |
|
э |
2h b |
|||
|
|
|||
|
|
|
||
Гидравлическим радиусом называется отношение площади живого сечения потока к смоченному периметру: R / .
Геометрический и гидравлический радиусы - совершенно разные понятия, даже в случае напорного течения жидкости в круглой трубе. При гидравлических расчетах часто используется понятие эквивалентного диаметра dэ, который равен 4R.
4.2. Уравнение расхода. Условие неразрывности потока.
22
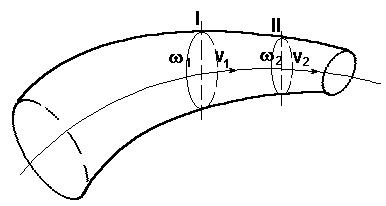
Условие неразрывности выражает закон сохранения материи. Рассмотрим установившееся движение жидкости в жестком русле переменного потока. Выберем 2 произвольных сечения I и II, нормальных к оси потока, и рассмотрим заключенный между ними участок. Через сечение I за время t на участок I-II поступит масса жидкости m1, а через сечение II за это же время выйдет масса m2. Согласно закону сохранения энергии m2 должна быть равна m1. Массы жидкости можно выразить в виде объемов, прошедших че-
рез сечения I и II за время t: |
m1 1Q1 t; |
m2 2Q2 t. |
Т.е.: |
|
|
|
1 |
Q |
1 |
|
2 |
Q |
2 |
- уравнение постоянства расхода сжимаемой жидкости. Для |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
несжимаемой |
|
жидкости: |
|
1 |
|
2 |
const. |
Следовательно, |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Q |
1 |
Q |
2 |
Q const - это уравнение называется уравнением постоянства |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
расхода для несжимаемой жидкости. Из него следует, что при установившемся движении несжимаемой жидкости расход в любом сечении потока постоянен.
Т.к. Q v, то уравнение постоянства расхода может быть записано следующим образом: 1v1 2v2 v const.
Данное уравнение называется условием неразрывности потока. Оно показывает, что при установившемся движении несжимаемой жидкости произведение площади живого сечения на среднюю скорость потока является
постоянной |
|
величиной. Из условия неразрывности потока следует, что |
||||
v |
/ v |
|
2 |
/ |
1 |
, при установившемся движении несжимаемой жидкости |
1 |
2 |
|
|
|
||
средние скорости потока обратно пропорциональны площадям, соответствующих живых сечений. Для сжимаемых жидкостей условие неразрывно-
сти потока имеет вид: |
|
|
1 |
v |
|
2 |
v . |
|
1 |
|
1 |
2 |
2 |
23
ЛЕКЦИЯ 5 Уравнение Бернулли.
5.1. Общие сведения. Виды энергии движущейся жидкости.
Механическая энергия состоит из потенциальной и кинетической энергий. В свою очередь потенциальная энергия жидкости делится на энергию положения и энергию давления. Т.е. полная механическая энергия потока
жидкости: E=Eполож+Едавл+Екин.
Удельной энергией потока называется энергия, приходящаяся на единицу силы тяжести или массы жидкости:
|
|
|
|
|
|
|
|
|
|
e E / G или e E / m, |
|
|
|
|
|
(1) |
|||||
где E- энергия, G - вес и m - масса жидкости. |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
Дж |
Нм м; |
|
|
|
Нм |
к гм |
2 |
м |
2 |
|||
e |
|
E |
/ |
G |
e |
|
. |
||||||||||||||
|
|
|
|
|
Н |
Н |
|
к г |
с |
2 |
к г |
с |
2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
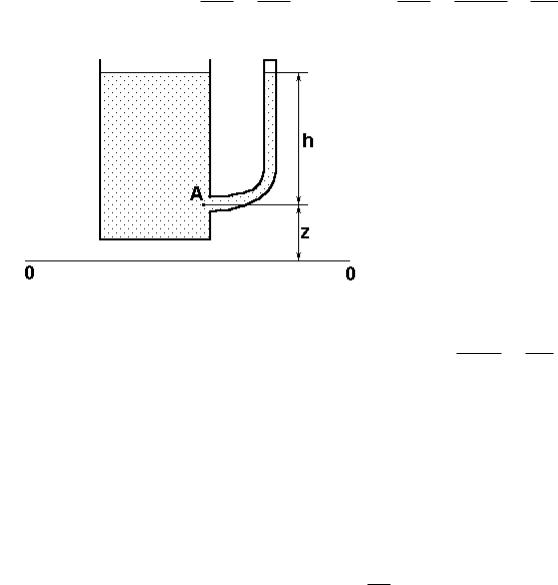
Подсчитаем удельную энергию для частицы жидкости, отнесенную к весу жидкости. Возьмем сосуд наполненный жидкостью (рис. 1). Определим энергию положения жидкой частицы
в точке А с координатой z. Если сила тяжести частицы G, то ее энергия положения над плоскостью 0-0 будет:
E |
Gz , а удельная энергия положения: |
|
п о л |
e Eп о л Gz z. (2)
G G
Т.е. удельная энергия положения, приходящаяся на единицу силы тяжести, равна геометрической высоте над плоско-
стью сравнения.
Определим удельную энергию давления. Частица жидкости в точке А находится под избыточным давлением окружающей жидкости р= gh, поэтому если от уровня этой точки вывести пьезометр, то частица может в нем подняться на высоту h=p/ g. Следовательно, энергия давления:
Eд авл Gh G pg ,
а удельная энергия давления, отнесенная к весу частицы:
24
e |
|
|
Eд авл |
p/ g. |
(3) |
||
д авл |
|
||||||
|
|
|
G |
|
|
||
|
|
|
|
|
|
||
Сумма удельной энергии положения и удельной энергии давления да- |
|||||||
ет |
|
|
|
|
|
|
|
удельную потенциальную энергию: |
e |
|
z p/ g. По рисунку нетрудно |
||||
|
|
|
|
|
п о т |
|
|
установить, что для любой частицы жидкости, находящейся в сосуде, удельная потенциальная энергия равна расстоянию от плоскости сравнения 0-0 до уровня жидкости в пьезометре.
Подсчитаем величину удельной кинетической энергии жидкой частицы массой m. Кинетическая энергия, как известно, может быть выражена
формулой:
Eк ин mu |
2 |
/ 2, |
тогда удельная ки- |
|
нетическая энергия
|
|
E |
|
mu |
2 |
|
u |
2 |
|
e |
|
к ин |
|
|
|
. |
|||
|
|
|
|
|
|||||
|
к ин |
G |
2mg |
|
2g |
|
|||
|
|
|
|
||||||
(4)
Величину екин можно измерить, если опустить в движущуюся жидкость трубку, изогнутую навстречу движению жидкости (рис. 2). Уровень жидкости в трубке поднимется выше уровня свободной поверхно-
рис. 2 сти потока на величину u2/2g, т.е. движущаяся жидкость будет ока-
зывать дополнительное давление на величину екин. Такая трубка называется трубкой Пито.
Таким образом:
e z p/ g u |
2 |
/ 2g . |
(5) |
|
|
||||
Отметим, что уравнение (5) справедливо, только для случая несжимае- |
||||
мой жидкости. В более общем виде: |
|
|
|
|
e z (p) / g u |
2 |
/ 2g, |
(6) |
|
|
||||
где (р) определяется из интегрального соотношения
|
p |
dp |
|
|
(p) |
|
. |
||
(p) |
||||
|
p |
|
||
|
|
|
||
|
0 |
|
|
(7)
5.2.Уравнение Бернулли для идеальной жидкости. Уравнение Бернулли для течений сжимаемых невязких жидкостей.
Уравнение Бернулли является вторым основным уравнением гидродинамики и выражает закон сохранения энергии. Уравнение Бернулли устанавливает связь между скоростью, давлением и потерями энергии потока жид-
25
кости. Уравнение Бернулли применимо только для течений с плавноизменяющимся движением.
Если силы трения отсутствуют, потери энергии будут равны 0. Для элементарной струйки идеальной жидкости или невязкой сжимаемой жидкости согласно закону сохранения энергии полная удельная энергия должна оставаться неизменной (см. рис. 3), т.е.
z (p) / g u |
2 |
/ 2g |
const. |
|
(8)
рис. 3
Случай 1. Движение элементарной струйки идеальной жидкости. Так как =сonst, то
|
|
p |
dp |
|
p p |
|
|
|
|||
|
|
|
0 |
||
Ф p |
|
|
|||
|
|
p |
|
|
|
|
|
0 |
|
|
|
и формула (8) принимает вид:
|
|
|
p |
u 2 |
|
|
|
p |
|
z |
1 |
|
1 |
|
1 |
z |
2 |
|
2 |
|
|
|
|||||||
|
|
|
2g |
|
|
|
|||
|
|
|
|
|
|
||||
|
p |
const , |
|
|||
|
|
|||||
|
|
|
|
|
||
|
u2 |
2 |
const |
(9) |
||
2g |
||||||
|
|
|
||||
это равенство называется уравнением Бернулли для элементарной струйки идеальной жидкости. Отдельные члены равенства (9) имеют размерность длины и называются соответственно: U2/2g - скоростной, p/ - пьезометри-
ческой, z - нивелирной высотами. Сумма этих высот Н называется гидравлической высотой.
Уравнение (9) приводит к классической формулировке теоремы Бернулли: при стационарном движении тяжелой идеальной несжимаемой жид-
26
кости гидравлическая высота, равная сумме скоростной, пьезометрической и нивелирной высот сохраняет постоянное значение вдоль линии тока (траектории).
Случай 2. Изотермическое течение.
Как было выяснено в лекции 2, в этом случае связь плотности и давления определяется уравнением Менделеева-Клапейрона:
p RT
.
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
dp |
|
RT |
|
p |
|
|
RT |
|
|
|
|
|
|
|
|
|
|
|
lnp const . |
||
Ф p |
|
p |
|
ln |
|
|
|
|||||
|
|
|
p0 |
|
p0 |
|
|
|
||||
Значит, уравнение (8) принимает вид:
U |
2 |
|
RT |
|
|
|
gz |
ln p const |
|||
2 |
|
||||
|
|
||||
(вдоль линии тока) |
(10) |
Случай 3. Политропное течение.
В этом случае (опять же см. лекцию 2)
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
. |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Значит |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
dp |
|
1 |
p |
dp |
|
p |
|
1 |
|
p |
|
|||||
|
|
|
|
|
p |
|
|
|
|
|
|
|||||||||
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|||||
Ф р |
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
p |
|
|
|
|
|
|
|
p |
|
1 |
|
|
||||
|
|
|
p |
|
0 |
p |
p |
|
|
|
0 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, уравнение (10) принимает вид:
p
1
const
.
U2 |
p |
|
|
||||
|
gz |
|
|
|
const |
(вдоль линии тока). (11) |
|
2 |
1 |
||||||
|
|
|
|||||
Этому уравнению можно придать другой вид. Из уравнения Менделее- ва-Клапейрона
pRT
.
Теперь уравнение (11) можно записать так: |
|
|||||||
|
U2 |
|
RT |
|
|
|||
|
|
gz |
|
|
|
const |
(вдоль линии тока). (12) |
|
2 |
1 |
|
||||||
|
|
|
||||||
Выписанные выше уравнения (9)-(12) справедливы вдоль элементарной струйки жидкости (линии тока). Однако, в случае течения идеальной жидкости по трубе эти уравнения будут выполняться для каждой точки потока. Действительно, продольная скорость движения идеальной жидкости не
27
зависит от поперечной координаты в связи с отсутствием трения. Имеет место уравнение (9), справедливое для любой точки потока. Из него автоматически следует, что в любой точке потока жидкости по горизонтальной трубе постоянного сечения скорость и давление одинаковы. Это означает, что продольный перепад давления отсутствует. Это понятно, так как для движения идеальной жидкости не требуется силы. Так как трения нет, полная механическая энергия сохраняется.
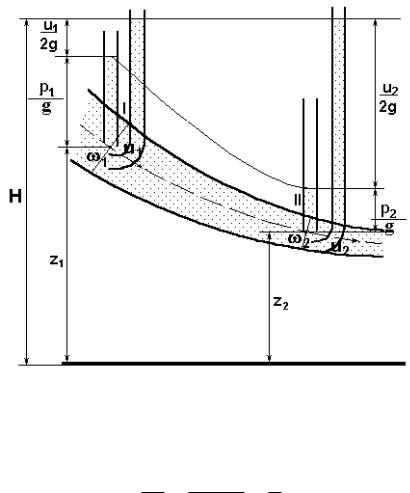
Энергетический смысл уравнения Бернулли для элементарной струйки или для течения идеальной жидкости в трубе при установившемся движении заключается в том, что полная удельная механическая энергия вдоль потока остается неизменной. Следовательно, уравнение Бернулли выражает закон сохранения механической энергии при движении идеальной жидкости: сумма потенциальной и кинетической энергии при движении идеальной жидкости неизменна. Изменение одного вида потенциальной или кинетической энергии всегда приводит к противоположному изменению другого.
Т.к. площадь живого сечения элементарной струйки II меньше площади I скорость u2, будет большей u1, а давление p2<p1. Следовательно, увеличение удельной кинетической энергии в сечении II происходит за счет уменьшения удельной потенциальной энергии.
Поясним геометрический смысл уравнения Бернулли для движения идеальной жидкости. Слагаемые z1 и z2 представляют собой геометрический напор, т.е. высоту расположения центра тяжести данного сечения над некоторой плоскостью сравнения 0-0.
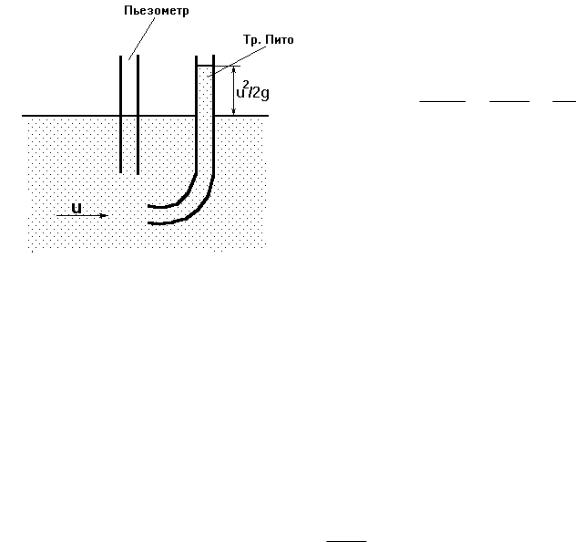
Второе слагаемое - пьезометрический напор, соответствует гидростатическому давлению в рассматриваемой точке. Т.е. пьезометрический напор это расстояние от центра тяжести живого сечения элементарной струйки до уровня жидкости в пьезометре.
Третье слагаемое u2/2g называется скоростным напором, который замерен с помощью трубки Пито. Уровень жидкости в трубке Пито устанавливается выше уровня жидкости в пьезометре на величину скоростного напора u2/2g.
Следовательно, геометрический смысл уравнения Бернулли для элементарной струйки идеальной жидкости состоит в том, что сумма трех напоров - геометрического, пьезометрического, скоростного - есть величина постоянная. Умножив уравнение (9) на g получим уравнение Бернулли, все члены которого измеряются в единицах давления (Па):
gz p U |
2 |
/ 2 |
const, |
|
(13)
где gzвесовое давление; р- гидростатическое давление; U2/2- динамическое давление.
Из этого уравнения следует, что для давления горизонтального напорного потока справедливо положение: где больше v, там меньше давление и, наоборот, где больше р, там меньше v.

28
5.3. Уравнение Бернулли для течений вязкой жидкости по трубам.
При течении вязкой жидкости положение существенно изменяется. Присутствие силы трения приводит к потерям полной механической энергии и зависимости скорости от поперечной координаты. Однако и в этом случае можно пользоваться теоремой Бернулли, если учесть энергетические потери на трение. Делается это следующим образом.
Рассмотрим течение вязкой несжимаемой жидкости по трубе между двумя сечениями 1 и 2. Для идеальной жидкости в подобном случае выполняется уравнение (9), которое можно записать, применив его к тому и другому сечению, в виде
U |
2 |
|
|
|
p |
|
|
1 |
z |
|
|
1 |
|||
|
|
|
|||||
2g |
1 |
|
|||||
|
|
||||||
|
|
|
|||||
U 2 2g2
z 2
|
p |
|
|
2 |
|
|
||
|
,
где U1 и U2 - скорости, р1 и р2 - давления в сечениях 1 и 2 соответственно, z1, z2 - координаты этих сечений.
Уравнение Бернулли для вязкой жидкости имеет вид:
|
V2 |
|
|
|
p |
1 |
|
1 |
1 |
z |
1 |
|
|
||
2g |
|
||||||
|
|
||||||
|
|
|
|||||
|
|
2 |
V2 |
|
|
|
p |
2 |
|
|
2 |
z |
2 |
|
|
||
|
2g |
|
||||||
|
|
|
|
|||||
|
|
|
|
|
||||
h
т р
hм
,
(14)
где V1 и V2 - средние скорости, р1 и р2 - давления в сечениях 1 и 2 соответственно, z1, z2 - координаты этих сечений, hтр - потери напора (энергии) на трение, произошедшие при движении жидкости между двумя сечениями,hм - потери напора на местных сопротивлениях (поворот, расширение потока, сужение, колено, вентиль и пр.), - коэффициент кинетической энергии (Кориолиса), отвечающий за однородность профиля (интенсивность вихря). В случае ламинарного течения =2, а турбулентного, где профиль скорости более однороден и вихрь менее интенсивен, =1,1. Таким образом, уравнение Бернулли для вязкой жидкости учитывает потери напора на трение вследствие вязкости (вводится h) и тот факт, что движение является вихревым (вводится ). Аналогичным образом “поправляются” и другие уравнения:
при изотермическом течении
|
V |
2 |
|
|
|
RT |
|
|
|
|
|
V |
2 |
|
|
|
|
|
|
|
2 |
|
|||||
1 |
1 |
z |
|
|
|
ln p |
|
|
|
2 |
|||
2g |
|
1 |
g |
1 |
|
2g |
|
||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||
z |
|
|
RT |
ln p |
|
h |
|
2 |
g |
2 |
|||||
|
|
|
|
||||
|
|
|
|
|
|
т р
hм
,
(15)
при политропном процессе
|
|
V |
2 |
|
|
|
|
p |
|
|
|
|
|
V |
2 |
|
|
|
|
p |
|
|
1 |
|
|
|
|
1 |
|
2 |
2 |
|
|
|
2 |
||||||||||
|
1 |
z |
|
|
|
|
|
|
|
z |
|
|
|
|
||||||||
|
2g |
|
1 |
1 g |
|
|
2g |
|
2 |
1 g |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5.4. Напорные и пьезометрические линии.
h
т р
hм
.
(16)
29
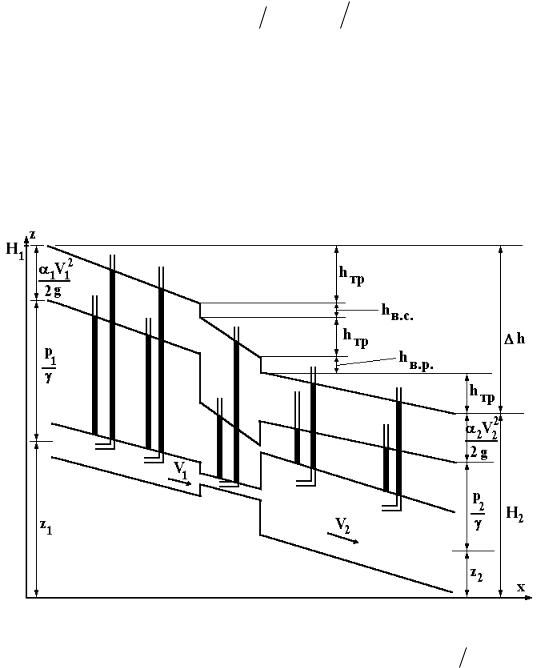
На практике при исследовании трубопроводов, как правило, строятся напорные и пьезометрические линии. Они дают наглядное представление о потерях, о переходе одного вида энергии в другой по длине потока и позволяют при решении многих задач установить значение, причины и степень изменяемости основных параметров движения жидкости. Эти линии строятся в соответствии с правилами, вытекающими из уравнения Бернулли (14).
Напорная линия показывает полный напор в каждом сечении потока. Геометрически напорная линия является графиком, изображающим зависи-
мость гидравлической высоты
z p V |
2 |
2g |
|
от местоположения сече-
ния. Так как полный напор является по своему смыслу полной механической энергией, а в силу закона сохранения она не может увеличиваться, то напорная линия не может повышаться. Более того, в силу потерь энергии на трение, механическая энергия необратимо переходит в тепловую, значит, напорная линия только понижается вниз по потоку. Только в том случае, когда в трубопроводе существует источник энергии (насос, вентилятор), напорная линия в месте его расположения повышается.
Пьезометрическая линия показывает пьезометрический напор в каждом сече-
нии потока. Геометрически пьезометрическая линия изображающим зависимость пьезометрической высоты
является графиком,
z p |
от местопо- |
ложения потока. Так как по физическому смыслу пьезометрический напор является потенциальной энергией потока, а она может переходить в кинетическую и наоборот, то пьезометрическая линия может не только понижаться, но и повышаться по течению. Это происходит, например, при расширении потока и объясняется уменьшением скорости и, соответственно, кинетиче-

30
ской энергии, часть которой переходит в потенциальную энергию. Иными словами, понижение скорости потока приводит к возрастанию давления (в полном соответствии с (14)).
Если истечение жидкости происходит в атмосферу, значит, в выходном сечении давление становится минимально возможным (атмосферным) и потенциальная энергия потока равна только потенциальной энергии тяготения. Следовательно. в этом случае пьезометрическая линия проходит через центр поперечного выходного сечения. Если же давление в канале меньше атмосферного, пьезометрическая линия идет ниже оси канала.
Так как напорная линия является графиком полной механической энергии, а пьезометрическая - только потенциальной, напорная линия всегда идет выше пьезометрической. Расстояние между напорной и пьезометрической линиями есть кинетическая энергия потока. На участках постоянного сечения скорость и кинетическая энергия не меняются, поэтому напорная и пьезометрическая линии следуют параллельно друг другу. Наклон этих линий больше там, где больше трение, то есть на участках, где сечение меньше.
Вточках, где находятся какие-либо местные сопротивления, в которых происходит потеря энергии (заслонки, вентили, резкое сужение, расширение потоков и пр.), напорная и пьезометрическая линии испытывают скачок.
Вконфузорных (сходящихся) патрубках напорная и пьезометрическая линии расходятся, в диффузорных (расходящихся) - сходятся. В баках и водоемах, где жидкость не движется, линии энергии совпадают со свободной поверхностью, если она находится под атмосферным давлением.
Наконец, пьезометрическую линию можно провести, установив пьезометры и соединив уровни жидкости в них, а напорную - через уровни жидкости в трубках Пито, установленных в точках, где скорость потока равна средней.
Подробная схема построения и физического смысла различных участков и отрезков напорной и пьезометрической линий приведена на рисунке.
Здесь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
1 |
V2 |
|
|
|
|
|
|
p |
|
|
2 |
V2 |
H |
1 |
z |
1 |
|
1 |
|
|
1 |
, |
H |
2 |
z |
2 |
|
2 |
|
|
2 |
||
|
|
2g |
|
|
2g |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
- полные напоры во входном и выходном сечении, z1, z2 - вертикальные координаты сечений, р1,р2 - давления жидкости в них, V1,V2 - скорости.
Закон сохранения энергии иллюстрируется на рисунке выполнением
равенства
H1 H 2 h,
где h hтр hв.с. hтр hв.р. hтр - полные потери напора (энергии)
по потоку, состоящие из потерь на трение (hтр) и потерь в местных сопротивлениях: на внезапное сужение (hв.с.) и внезапное расширение (hв.р.).
