
Ющубе_КОНСПЕКТ ЛЕКЦИЙ по МЕХАНИКИ ГРУНТОВ ТГАСУ
.pdf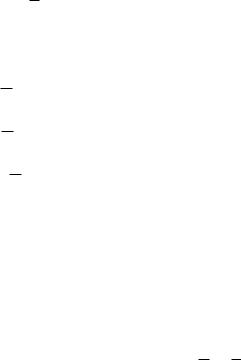
Если для рассматриваемой точки M (рис. 6.7) угол видимо-
сти обозначить через α, а
=
2
+ |
/ |
|
, где
|
/ |
|
– угол между крайним
лучом и вертикалью, то напряженное состояние в точке M будет определяться следующими выражениями:
z
y
=P ( + sin cos 2 )
=P ( − sin cos 2 )
= P (sin sin 2 ).
; ;
(6.14)
Как видно из выражений (6.14), все составляющие напряжений z, y, в рассматриваемой плоскости ZOY не зависят от деформационных характеристик полупространства и легко табулируются для действия единичной силы P, т. е.
|
z |
= K |
P; |
|
y |
= K |
y |
P; |
|
z |
|
|
|
|
=
K |
zy |
P |
|
|
.
(6.15)
Значения коэффициентов Kz, Ky, Kyz сведены в специальные
таблицы в зависимости от относительных координат
Z b
и
y b
рас-
сматриваемой точки.
Для практических целей наибольший интерес представляют составляющие напряжений z. Характер их распределения под полосовой нагрузкой приведен на рис. 6.8.
Пользуясь формулами (6.15), можно построить линии равных напряжений (изобары) в массиве под полосовой нагрузкой (рис. 6.9)
Как видно из рис 6.9, сжимающие напряжения z интенсивностью 0,1Р, определяющие вертикальные перемещения фундаментов, развиваются до глубины 6ƅ, тогда как горизонтальные напряжения y и касательные – zy имеют развитие соответственно на глубины 1,5b и 2,0b.
81
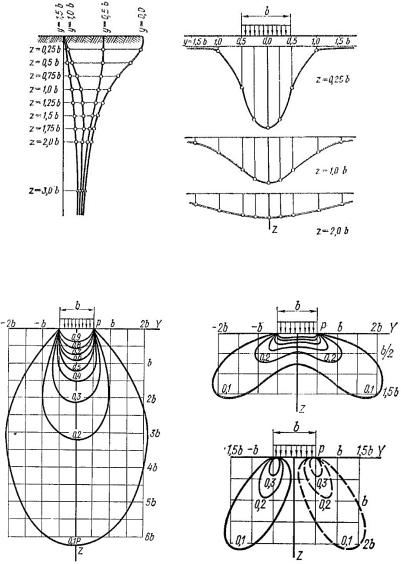
Рис. 6.8. Составляющие напряжений z. Характер их распределения под полосовой нагрузкой [11]
а |
б |
в
Рис. 6.9. Линии равных напряжений в линейно-деформируемом полупространстве под полосовой нагрузкой:
а – напряжения z; б – y; в – zy [11]
82
Наибольшие и наименьшие, а значит, главные напряжения будут иметь место на вертикальной оси симметрии полосовой нагрузки (рис. 6.10).
Рис. 6.10. Эллипсы напряжений при действии полосовой нагрузки [11]
Действительно, для таких площадок |
/ |
= − |
|
, а = |
|
− |
|
= 0, |
||||
|
|
|
||||||||||
|
2 |
2 |
2 |
|||||||||
|
|
|
|
|
|
|
|
|
||||
тогда = |
P |
(sin sin 2 ) = 0 |
, т. е. площадки главные. Значения глав- |
|||||||||
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
ных напряжений будут равны:
|
|
= |
P |
( + sin ); |
|
|
|
|
|||
1 |
|
|
|||
|
|
|
|
||
|
|
|
P |
|
|
|
|
= |
|
|
|
2 |
|
( −sin ). |
|||
|
|
|
|
|
|
|
|
|
|
|
|
(6.16)
Главными площадками будут также площадки, расположенные по биссектрисам углов видимости, и площадки, им перпендикулярные.
В справочной литературе приводится решение по определению напряжений от действия треугольной нагрузки. В совокупности решения для прямоугольной и треугольной нагрузки позволяют определять напряжения в грунтовом массиве для весьма широкого круга инженерных сооружений.
83
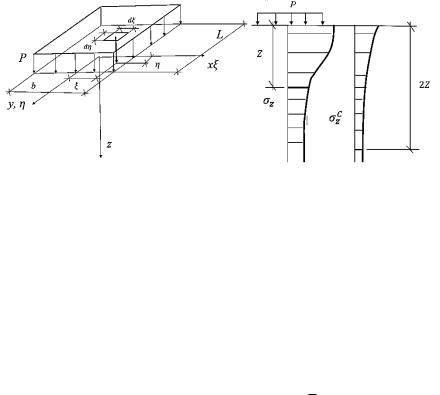
6.3. Случай загрузки прямоугольной площадки поверхности основания равномерно распределенной нагрузкой
Вертикальные составляющие напряжений
z
получены
А. Лявом из решения для сосредоточенной силы (задача Буссинеска) путем замены сосредоточенной силу P на распределенную по элементарной площадке Рd d (рис. 6.11) в результате
ее двойного интегрирования в пределах ширины b и длины L прямоугольной нагрузки.
Рис. 6.11. Равномерно распределенная нагрузка по площади прямоугольника
Значения этих напряжений под центром и углом прямоугольной загрузки определяются по формулам:
z = P; |
(6.17) |
c |
= |
|
P, |
(6.18) |
z |
4 |
|||
|
|
|
|
где – табличный коэффициент, принимаемый в зависимости от
соотношения сторон площади загрузки = l и относительной b
84
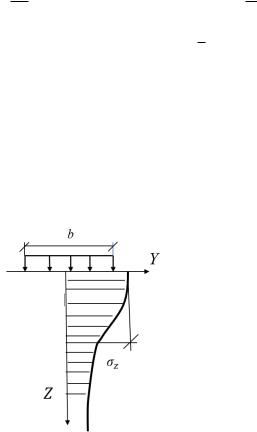
глубины, равной
= |
2Z |
|
b |
||
|
– при определении
z
и |
|
=Z b
– при
определении
напряжений
с z
z
. При соотношении сторон |
= |
l |
10 |
значения |
|
b |
|||||
|
|
|
|
близки к напряжениям, соответствующим за-
грузке в виде бесконечно длинной полосы шириной b, т. е. плоской задаче.
Характерная эпюра напряжений
z
под центром прямо-
угольной загрузки представлена на рис. 6.12. При Z = 0 значенияz = P с глубиной напряжения z уменьшаются, асимптотически
приближаясь к нулю.
Рис. 6.12. Эпюра z под центром прямоугольной нагрузки
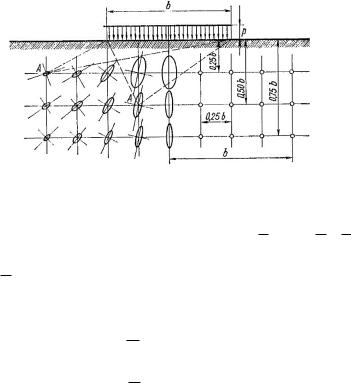
Если необходимо определить напряжения |
z |
не под цен- |
тром загрузки, а в любой другой точке, достаточно эту точку сделать угловой и найти алгебраическую сумму напряжений под угловыми точками от загрузки соответствующих прямоугольников (рис. 6.13). Решение, имеющееся для угловых точек, оказывается очень удобным для практических расчетов.
85
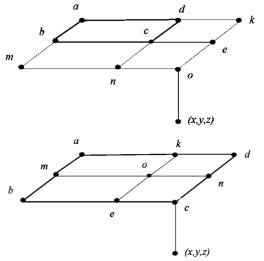
а
б
Рис. 6.13. Схема определения напряжений способом угловых точек:
а – точка (О) находится внутри площади загружения; б – точка (O) находится вне площади загружения
Для случая а (рис. 6.13)
|
z(0) |
= |
z |
(okam)+ |
z |
(okdn)+ |
z |
(ombe)+ |
z |
(once). |
|
|
|
|
|
|
(6.19)
Для случая б (рис. 6.13)
|
z(0) |
= |
z |
(okam)− |
z |
(okdn)− |
z |
(oebm)+ |
z |
(oecn). |
|
|
|
|
|
|
(6.20)
6.4.Влияние площади загрузки
инеоднородности основания на распределение напряжений
Рассмотрим случай действия равномерно распределенных нагрузок одной и той же интенсивности P, но разной ширины b1 > b2 (рис. 6.14).
86
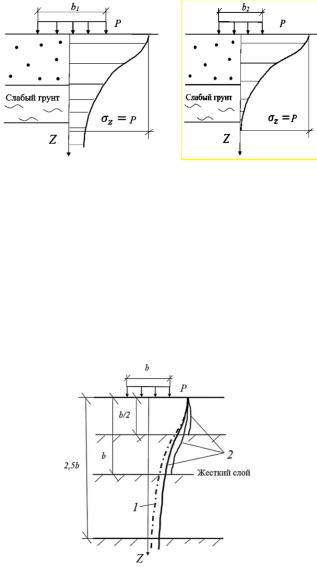
Рис. 6.14. Влияние ширины полосы загружения на глубину распространения напряжений z
Как видно из рис. 6.14, при большей ширине приложения нагрузки затухание напряжений с глубиной происходит медленнее. Осадка в этом случае будет больше, особенно если в пределах активной зоны распространения z попадет слабый слой.
В случае если основание неоднородное и в пределах активной зоны расположен жесткий слой, то наличие этого слоя вызывает концентрацию напряжений z (рис. 6.15).
Рис. 6.15. Распределение напряжений z:
1 – для однородного основания; 2 – при различной толщине сжимаемого слоя, подстилаемого жестким
87
Из рис. 6.15 видно, что чем меньше сжимаемый слой и ближе жесткий слой к нагрузке, тем больше концентрация напряжений. Решения, учитывающие наличие жесткого слоя, получены К.Е. Егоровым и др. Анализ этих решений показывает, что учет неоднородности основания следует производить, когда различие в деформационных характеристиках достаточно велико, например, когда глинистые грунты подстилаются скальными или полускальными.
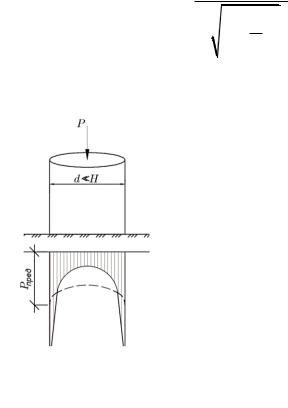
6.5. Распределение давлений по подошве сооружений, опирающихся на грунт (контактная задача)
Вопрос о распределении давлений по подошве сооружений имеет большое практическое значение, особенно для гибких фундаментов, рассчитываемых на изгиб.
Если известно реактивное (контактное) давление по подошве фундамента, то, приложив к подошве фундаментной балки или плиты его обратную величину, можно найти расчетные изгибающие моменты и перерезывающие силы с помощью обычных уравнений статики.
Большинство фундаментов сооружений обладает определенной (конечной) жесткостью. Поэтому важно оценить, как жесткость фундамента сказывается на распределении контактных давлений и давлений в массиве грунта.
Исходным уравнением для решения контактной задачи для жесткого штампа является формула Буссинеска для вертикальной деформации линейно-деформируемого полупространства от действия сосредоточенной силы P:
ωz = P/πCR, |
(6.21) |
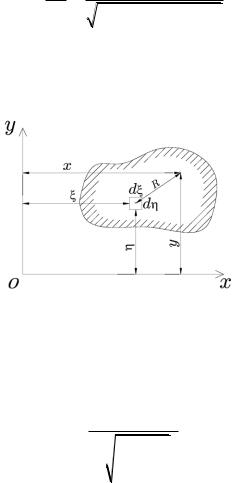
где C – коэффициент линейно-деформируемого полупространства. Для произвольной площади загружения (рис. 6.16) будем
иметь:
88
z = |
1 |
|
(ξ, η)dξdη |
. |
||
C |
x – ξ 2 + |
y – η 2 |
||||
|
F |
|
||||
|
|
|
|
|
||
(6.22)
Поскольку фундамент абсолютно жесткий, то все точки его площади подошвы будут иметь при центральной нагрузке одну и ту же вертикальную деформацию, т. е. z = const.
Рис. 6.16. Схема площади загрузки произвольного вида [11]
Решение интегрального уравнения (6.22) для круглого абсолютно жесткого фундамента при центральном загружении имеет вид
P |
= |
|
xy |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
P |
|
|
|
|
|
m |
|
|
|
|
|
2 |
|
|
1− |
|
|
||
|
|
|
||
|
|
|
||
|
r |
|
||
|
|
|
|
|
,
(6.23)
где r – радиус подошвы фундамента; ρ – расстояние от центра подошвы до любой ее точки ( r ); Pm – среднее давление на еди-
ницу площади подошвы Pm = P/F.
Для случая плоской задачи (абсолютно жесткая лента и центральное загружение):
89
P |
= |
|
|
xy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2P |
|
|
|
|
|
m |
|
|
|
|
|
|
|
y |
|
2 |
|
|
|
|
|||
1− |
|
|
|
|
|
b |
|
|
|||
|
|
|
|||
|
1 |
|
|
||
|
|
|
|
|
|
,
(6.24)
где y – расстояние по горизонтали от середины фундамента до рассматриваемой точки; b1 – полуширина фундамента.
Эпюра напряжений (сплошная линия) будет иметь вид (рис. 6.17):
– для круглого фундамента при = 0 Pxy = Pm/2;
при = r Pxy → ;
– для ленточного фундамента при y = 0 Pxy = 2Pm/ ;
при y = b1 Pxy → .
Однако из условия прочности грунта следует, что контактные давления не могут быть больше предельных. Фактическая эпюра контактных давлений будет распределяться по более пологой кривой и у края не будет превышть предела несущей способно-
сти грунта (пунктирная линия на рис. 6.17).
Непосредственные измерения контактных давлений показывают, что при возрастании нагрузки на фундамент происходит постепенная их трансформация от седлообразного вида – при небольших нагрузках до параболического – при нагрузках, близких к предельным.
Фактические фундаменты обладают определенной жесткостью. Гибкость фундаментов, по проф. Горбунову-Посадову, оценивается показателем гибкости r; при r = 0 фундамент абсолютно жесткий. С возрастанием показателя r гибкость фундамента уве-
90
