Ющубе_КОНСПЕКТ ЛЕКЦИЙ по МЕХАНИКИ ГРУНТОВ ТГАСУ

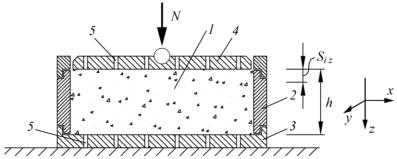
онных приборах. Компрессионный прибор представляет собой жесткую обойму (кольцо), в которую помещается образец грунта. В нижней части прибора размещается поддон (база) (рис. 3.7).

Рис. 3.7. Схема компрессионного прибора:

1 – грунт; 2 – жесткая обойма; 3 – поддон; 4 – поршень-штамп; 5 – фильтрующие отверстия

Нагрузка на образец грунта передается через жесткий пор- шень-штамп. В поддоне и в поршне-штампе предусмотрены отверстия для отвода воды, которая отжимается из грунта при его уплотнении. Грунт в приборе деформируется только в одном направлении. Боковое расширение грунта невозможно ( x = y = 0).

До начала испытаний образец грунта имеет высоту h. Сжимающие напряжения прикладываются к образцу грунта ступенями. Каждая последующая ступень прикладывается после достижения стабилизации осадки грунта Sz,i от предыдущей ступени. Исходя из допущения, что сжатие грунта происходит только за счет изменения объема пор, и зная начальный коэффициент пористости образца (е0), коэффициент пористости, соответствующий состоянию грунта на любой ступени нагружения (ei), может быть определен по следующим зависимостям:

41

где Vni, ni – соответственно изменение объема пор и пористости образца грунта.

Изменение объема пор образца грунта на ступени нагружения будет равно:

где A – площадь образца грунта.

Объем твердых частиц в образце грунта равен:

Подставляя значения соответствующих величин в формулу (3.1), будем иметь:

Сокращая подобные и представляя вертикальную относительную деформацию через z,i = Sz,i/h, будем иметь окончательно:

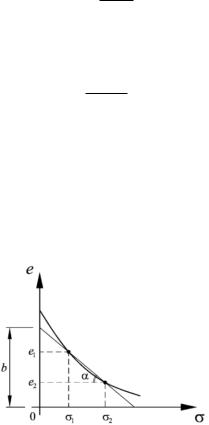
Используя эту основную зависимость, данные лабораторных испытаний можно представить в виде графика (рис. 3.8), который называют компрессионной кривой.

Рис. 3.8. Компрессионная кривая

42

Компрессионная кривая имеет нелинейный характер. Однако для практической оценки сжимаемости грунтов в случае небольшого изменения напряжений идут на спрямление компрессионной кривой. Тогда уравнение спрямленного участка приобретает вид

Параметр (b) отыскивается на оси (e), а угловой коэффициент (a) есть тангенс угла наклона спрямленного участка прямой к оси напряжений. Тогда

Так как коэффициент пористости – величина безразмерная, то коэффициент a, называемый коэффициентом уплотнения, имеет размерность [МПа-1].

Чем больше коэффициент уплотнения, тем более сжимаемый грунт.

Если:

a > 1 МПа–1 – грунт сильно сжимаемый; a < 0,01 МПа–1 – грунт мало сжимаемый.

По данным компрессионных испытаний можно определить модуль деформации грунта:

где – коэффициент, зависящий от коэффициента Пуассона грунта и учитывающий невозможность бокового расширения грунта при испытаниях в компрессионном приборе.

Характер деформаций грунта в компрессионном приборе соответствует условиям деформации бесконечно простирающегося слоя грунта, загруженного сплошной равномерно распределенной нагрузкой, с подстилающим практически не сжимаемым

43

слоем. Например, это ровный слой грунта под действием собственного веса. Поэтому для расчетов осадок фундаментов зданий и сооружений, имеющих ограниченные размеры в плане, следует использовать компрессионный модуль с соответствующими корректирующими коэффициентами, а для особо ответственных – штамповый модуль деформации.

3.3. Определение модуля деформации грунта испытаниями его штампом

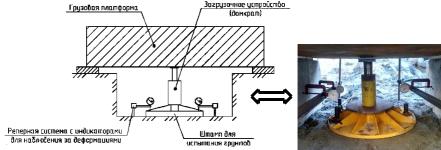
Схема испытания грунтов штампом и общий вид таких испытаний приведены на рис. 3.9.

Рис. 3.9. Схема (слева) и общий вид (справа) испытаний грунтов штампом

Нагрузка на штамп передается ступенями. Каждая последующая ступень нагружения прикладывается после достижения стабилизированной осадки штампа на предыдущей ступени нагружения. По результатам испытаний строят график (рис. 3.10).

Модуль деформации грунта определяется по формуле

где w – коэффициент, принимаемый для круглых жестких штампов равным 0,8; d – диаметр штампа; – коэффициент Пуассона;

44

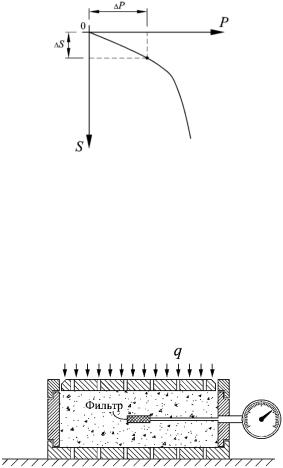
P – увеличение среднего давления под подошвой штампа на линейном участке кривой; S – приращение осадки.

Рис. 3.10. Зависимость осадки (S) штампа от давления на грунт (P)

Процесс консолидации водонасыщенных грунтов. Уплот-

нение полностью водонасыщенного грунта происходит не мгновенно, а во времени. Это связано с необходимостью оттока воды из пор грунта. Для фильтрации воды необходимо время, которое определяется водопроницаемостью грунта (см. подразд. 3.2).

Рассмотрим процесс испытания водонасыщенного грунта на сжатие в компрессионном приборе (рис. 3.11).

Рис. 3.11. Схема компрессионного прибора с датчиком порового давления

Давление в поровой воде измеряется с помощью иглы, имеющей на конце фильтр для пропуска только воды. Давление фиксируется, например, с помощью малорасходного манометра.

45

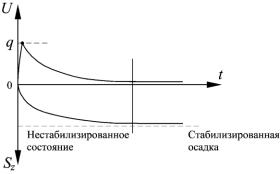
При быстром (мгновенным) приложении нагрузки q вода в первый момент времени (t = 0) не успевает начать фильтровать, а т. к. она практически несжимаемая, то осадка штампа будет равна нулю. Давление в поровой воде (U) в этот момент времени достигает максимального значения, а у глинистых грунтов текучей консистенции может быть равным нагрузке q, т. е. вся нагрузка передается на поровую воду (рис. 3.12).

Рис. 3.12. Графики изменения давления в поровой воде (U) и осадки штампа во времени (t)

Грунт в процессе консолидации находится в нестабилизированном состоянии. Условие равновесия грунта в этот период времени имеет вид

где z – напряжение в скелете грунта в момент времени t; U – избыточное давление в поровой воде в этот же момент времени.

В стабилизированном состоянии все давление передается на скелет грунта, т. е.

Из уравнений (3.9) и (3.10) следует, что напряжение в скелете грунта при нестабилизированном состоянии будет равно:

46

3.4. Коэффициент бокового давления грунта

Как уже было показано, в компрессионном приборе исключаются боковые деформации грунта. Однако в результате развития горизонтальных напряжений ( t = y) грунт давит на стенки жесткой обоймы. Для условия отсутствия поперечных деформаций ( x = y = 0) справедливо равенство

Откуда коэффициент бокового давления, представляющий собой отношение поперечных сжимающих напряжений к продольным, будет равен:

Коэффициент бокового давления определяют на приборах трехосного сжатия либо на специальных компрессионных приборах, оборудованных чувствительными жесткими обоймами для фиксации горизонтальных напряжений. По результатам многих исследователей, коэффициент для песков изменяется в пределах 0,4–0,6, а для глин – 0,7–0,75. Для водонасыщенных глинистых грунтов, находящихся в текучем состоянии, приближается к единице, т. е. имеет место гидростатический закон распределения напряжений:

Следует особо отметить, что использование коэффициента бокового давления возможно только в тех случаях и для решения таких инженерных задач, когда гарантируется отсутствие бокового расширения грунта.

3.5. Фильтрационные свойства грунтов

Как следует из предыдущего материала, для оценки развития осадки полностью водонасыщенного грунта во времени необходимо знать его фильтрационные свойства.

47

Первые эксперименты по изучению движения воды в грунтах были поставлены Дарси (1854 г.). Полученные им зависимости лежат в основе всех расчетов фильтрации грунтовых вод, а основная экспериментальная зависимость названа законом Дарси.

Введем понятие скорости фильтрации воды в грунте:

где Q – расход воды; A – площадь геометрического сечения, включая и часть сечения, заполненного частицами грунта.

Скорость фильтрации, определяемая по формуле (3.15), является фиктивной, т. к. в действительности вода движется в грунте по сложным извилистым каналам, учесть которые не представляется возможным.

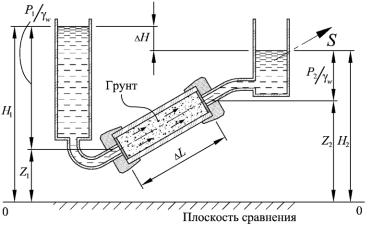
Рассмотрим схему движения воды в грунте (рис. 3.13).

Рис. 3.13. Схема движения воды в элементе грунта

Вода движется из области повышенных (H1) к области пониженных (H2) напоров. Предположим, что на элементарном участке грунта L движение воды направлено по оси S (рис. 3.13). Тогда зависимость Дарси можно записать в виде

48

Согласно этой зависимости, закон Дарси гласит: скорость фильтрации пропорциональна разности напоров H и обратно пропорциональна пути фильтрации L.

Отношение разности напоров к пути фильтрации есть градиент напора

где P – давление в воде; w – удельный вес воды; z – высота рассматриваемой точки над плоскостью сравнения.

Коэффициент kф в формуле (3.16) называется коэффициентом фильтрации. Если предположить, что градиент напора равен 1, тогда v = kф, т. е. коэффициент фильтрации численно равен 1,0 и измеряется в м/с или м/сут.

Графически закон Дарси представлен на рис. 3.14.

Рис. 3.14. Зависимость скорости фильтрации от градиента напора для песчаных грунтов

49

Зависимость скорости фильтрации от градиента напора, изображенная на рис. 3.14, характерна для песчаных грунтов. При этом следует иметь в виду, что закон Дарси в крупнозернистых материалах при больших скоростях движения воды может существенно нарушаться из-за перехода движения воды в турбулентный режим.

В плотных глинистых грунтах фильтрация воды имеет несколько иной характер. Движение воды в порах начинается лишь тогда, когда градиент напора превысит некоторую величину i0,

называемую начальным градиентом напора. Это объясняется тем, что свободная вода в глинистых грунтах защемлена пленочной связанной водой, которая препятствует началу фильтрации.

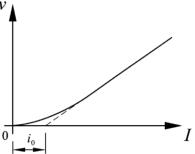
Зависимость скорости фильтрации от градиента напора для глинистых грунтов представлена на рис. 3.15.

Рис. 3.15. Зависимость скорости фильтрации от градиента напора для глинистых грунтов

Если предположить, что до начального градиента i0 движение воды через поры грунта не просиходит, то закон Дарси для глинистых грунтов будет выражаться формулой

Как видно из приведенных данных, наименее водопроницаемыми являются глинистые грунты. Если сравнить процесс раз-

50