
Ющубе_КОНСПЕКТ ЛЕКЦИЙ по МЕХАНИКИ ГРУНТОВ ТГАСУ
.pdf
что зоны сдвигов развиваются до глубины Z = 0,25b, где b – ширина фундамента.
Подставляя в формулу (8.8) значение Z = 0,25b, выражая величины, зависящие от угла внутреннего трения , через соответствующие коэффициенты, учитывая глубину подземной части здания и введя коэффициенты условия работ, будем иметь формулу, которая используется в практике проектирования:
R = |
|
c1 |
|
c2 |
|
|
|
|
, (8.10) |
|
|
||||||||
|
k |
|
|
M kzb II + M g d1 II + (Mq −1)db II + McсII |
|
||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
где с1 и с2 – коэффициент условий работы; k – коэффициент, принимаемый в зависимости от метода определения прочностных параметров и c; M , Mq, Mc – табличные коэффициенты, зависящие только от угла внутреннего трения; kz – коэффициент, принимаемый при b < 10 м равным kz = 1; b – ширина подошвы фундамента; II и 'II – удельные веса грунта соответственно выше и ниже подошвы фундаментов; сII – расчетное значение удельного сцепления грунта под подошвой фундамента; d1 – глубина заложения фундаментов; db – глубина подвала.
8.3. Предельная нагрузка для грунтов
Впервые эта задача была решена для невесомого грунта, нагруженного вертикальной полосообразной нагрузкой Прандтлем и Рейснером (1920–1921 гг.).
Получено точное очертание линий скольжения, которые имеют вид, показанный на рис. 8.3.
Формула для определения предельного давления на грунт
имеет вид |
|
|
|
|
qпред = ( d + сctg ) |
1 |
+ sin |
e tg − сctg . |
(8.11) |
|
|
|||
1 |
+ sin |
|
||
111
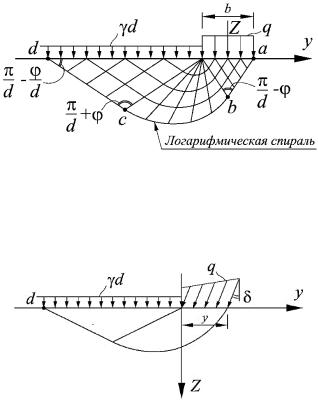
Рис. 8.3. Сеть линий скольжения в невесомом грунте при полосовой нагрузке
Для более общего случая наклонной нагрузки с учетом собственного веса грунта задача была решена проф. Соколовским в 1952 г. (рис. 8.4).
Рис. 8.4. Схема действия наклонной нагрузки на грунт
Получено очертание линий скольжения и формула для определения вертикальной составляющей qпр, удобная для практического применения в виде
qпр = N y + Nq d + Nc c,
где N , Nq , Nc – коэффициенты несущей способности, которые затабулированы в зависимости от и .
Горизонтальная составляющая предельного давления на грунт определяется по формуле qt = qпр tg .
112
Контрольные вопросы
1.Какие фазы напряженного состояния развиваются в основании штампа (фундамента) при возрастании нагрузки?
2.Какие характерные точки имеют место на графике зависимости осадки штампа от давления по его подошве?
3.Что такое начальное критическое давление на грунт и какой фазе напряженного состояния грунта под подошвой штампа оно соответствует?
4.Что такое расчетное сопротивление грунта и какой глубине развития зон сдвигов оно соответствует?
5.Что такое выпор грунта из-под подошвы фундамента
ик чему он приводит?
6.Какая фаза напряженного состояния формируется в основании штампа при достижении предельного давления под его подошвой?
7.Почему при проектировании и расчете фундаментов давление под их подошвой ограничивают расчетным сопротивлением грунта?
113
ЛЕКЦИЯ 9. УСТОЙЧИВОСТЬ МАССИВОВ ГРУНТОВ В ОТКОСАХ И СКЛОНАХ
Анализ устойчивости массивов грунта имеет большое практическое значение при проектировании земляных сооружений: насыпей, выемок, дамб, земляных полотен, больших котлованов и других подобных сооружений.
Задача устойчивости массивов является частной задачей общей теории предельного напряженного состояния грунтов, но имеет весьма существенные особенности.
Расчеты устойчивости массивов относятся к специальным разделам статики. Главные причины нарушения устойчивости земляных масс: эрозионные процессы; нарушение равновесия.
Эрозионные процессы протекают весьма медленно (зависят от метеорологических и физико-геологических условий) и в механике грунтов не рассматриваются.
Нарушение равновесия массивов грунтов – прямая задача механики грунтов. Нарушение устойчивости массивов грунтов проявляется в виде оползней, которые развиваются, как правило, в откосах или в естественных склонах при увеличении действующих на массив нагрузок или при уменьшении прочностных характеристик грунтов.
9.1. Устойчивость свободных откосов
Рассмотрим две элементарные задачи.
1.Устойчивость откоса из идеально сыпучего грунта, т. е.
0; с = 0.
На откосе свободно лежит твердая частица m. Вес частицы P. Разложим вес частицы P на нормальную к линии откоса силу N и касательную силу T (рис. 9.1). Сила T стремится сдвинуть частицу, но ей будет препятствовать сила трения T’, пропорциональная нормальной составляющей N, т. е.
114

T = P cos f,
где f – коэффициент трения.
Рис. 9.1. Схема сил, действующих на частицу откоса из идеально сыпучего грунта
Спроецируем все силы на наклонную грань откоса и будем иметь:
P sin – f P cos = 0, |
(9.1) |
откуда f = tg , а т. к. f = tg , то = .
Таким образом, предельный угол откоса сыпучего грунта равен углу внутреннего трения грунта. Этот угол назван углом естественного откоса сыпучего грунта. Для связного грунта он теряет смысл.
2. Устойчивость откоса идеально связного грунта,
= 0; с 0.
Допустим, что нарушение предельного равновесия произойдет при некоторой высоте вертикального откоса h и по поверхности ас, наклоненной к горизонту под углом .
Сторона предполагаемой призмы обрушения равна bс = h ctg , тогда вес погонного метра призмы (плоская задача) будет равен:
p = h2 ctg .
2
115
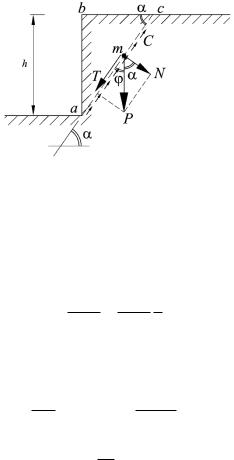
Разложим силу P на нормальную и касательную составляющие к поверхности ас (рис. 9.2). В нашем случае силами сопротивления скольжению будет только силы сцепления, распределенные по плоскости ас = h/sin .
Рис. 9.2. Схема сил, действующих на вертикальный откос из идеально связного грунта
Вточке с давление от веса призмы будет равно 0, а в точке
а– максимуму. Следовательно, в условии равновесия нужно учитывать только половину сил сцепления, т. е.
ac с 2
= |
h |
|
|
sin |
|
||
|
с 2
.
Тогда уравнения равновесия для призмы скольжения abc будет иметь вид
откуда
h2 ctg sin − 2
с = |
h |
sin |
|
2 |
|||
|
|
h |
= 0 , |
(9.2) |
sin2 |
||
2 . |
|
|
Высота h, соответствующая максимальному использованию сил сцепления с, будет при sin2 = 1 , что соответствует = 45 .
116

Тогда максимальная высота вертикального откоса идеально связного грунта будет равна:
h |
= |
2c |
. |
|
|||
k |
|
|
|
|
|
|
Критическая высота свободно стоящего откоса с с 0 будет определяться зависимостью
hk = |
|
( |
2c |
|
2 ) |
. |
|
|
|
||||
|
|
|
|
|||
|
tg |
|
45 − |
|
|
|
|
|
|
|
|
(9.3)
0;
(9.4)
9.2. Определение активного давления грунта на подпорные стенки
Рассмотрим простейший случай активного давления грунта на вертикальную подпорную стенку с идеально гладкой поверхностью, т. е. когда касательные напряжения на вертикальной поверхности равны 0.
Выделим элементарную призму грунта так, чтобы одна из ее граней совпадала с внутренней поверхностью подпорной стенки (рис. 9.3, а). Так как из условия касательные напряжения между грунтом и стенкой равны 0, тогда грани элементарной призмы будут в то же время главными площадками. При действии активных сил от собственного веса грунта и равномерно распределенной нагрузки всегда z > x, тогда " > ', учитывая, что z = z + q, где– удельный вес грунта, а z – координата элемента грунта, и воспользовавшись условием предельного состояния (4.18).
В случае несвязного грунта, т. е. с = 0:
x = ( z + q) tg2(45 – /2).
Интегрируя данное выражение по высоте подпорной стенки от 0 до h, получим равнодействующую активного давления (рис. 9.3, б)
117
h |
h |
γh2 |
|
|
E = |
|
σ |
dz = |
|
(γz + q)tg2 |
(45 −φ 2)dz = |
|
2 |
+ qh |
|
tg2 (45 − φ 2) , |
||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
|
|
a |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
окончательно |
E |
= |
|
|
|
|
+ qh |
|
tg |
(45 − 2) |
. |
|
||||||||||||||
|
|
|
|
|
||||||||||||||||||||||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
а |
|
|
|
|
|
|
|
|
|
б |
|
|
|
в |
|
|
|
|
|
г |
|
|
|
д |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(9.5)
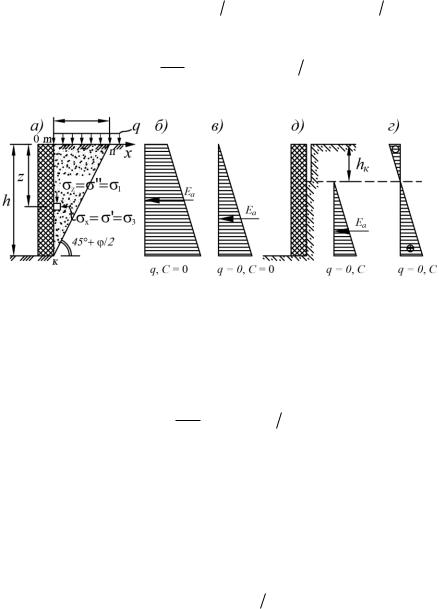
Рис. 9.3. Давления грунта на подпорную стенку [3]:
а – расчетная схема; б, в – эпюры активного давления несвязного грунта при наличии внешней нагрузки на грунт у стенки и её отсутствии соответственно; г, д – эпюры активного давления связного грунта
В случае отсутствия пригрузки (q = 0) и (с = 0) (рис. 9.3, в)
|
|
h |
2 |
E |
= |
|
|
|
|
||
a |
|
2 |
|
|
|
||
tg |
2 |
(45 − 2) |
|
.
(9.6)
Для связных грунтов при q = 0 и с 0 (рис. 9.3, г) решение приводит к тому, что в верхней части массива возникает отрицательное давление. Это происходит из-за того, что связный грунт может держать вертикальный откос (рис. 9.3, д). Критическая высота свободно стоящего вертикального откоса определяется по формуле (9.4.):
hk = |
2C |
, |
|
|
|||
tg(45 − 2) |
|||
|
|
118
а равнодействующая активного давления связного грунта на вертикальную стенку будет численно равна площади треугольника (рис. 9.3, д) или
|
|
|
h |
2 |
|
2 |
|
|
|
2C |
2 |
E |
|
= |
|
tg |
(45 − 2) |
− 2Ch(45 − 2) |
+ |
|
|||
|
|
|
|
|
|||||||
a |
2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
. (9.7)
9.3. Графоаналитический метод расчета несущей способности основания (метод
круглоцилиндрических поверхностей скольжения)
Данный метод является универсальным и применяется в тех случаях, для которых аналитические методы не разработаны.
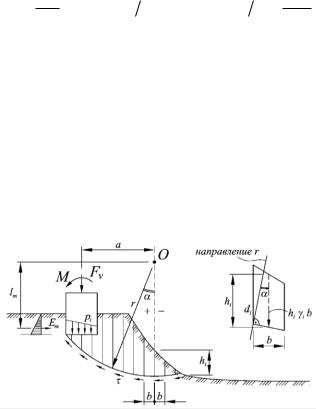
Наиболее часто этот метод используется для оценки устойчивости оснований фундаментов или сооружения в целом, расположенного на откосе или вблизи него (рис. 9.4).
Рис. 9.4. Расчетная схема к методу круглоцилиндрических поверхностей
Суть метода заключается в определении коэффициента устойчивости K, который для всех возможных поверхностей скольжения должен быть K 1,1–1,3.
Массив грунта, устойчивость которого определяют, разбивается на элементарные призмы шириной b и высотой hi. Удер-
119
живающими силами являются силы трения и силы сцепления грунта, развивающиеся в основании элементарных призм по предполагаемой поверхности скольжения. К сдвигающимcя силам относятся внешние воздействия, равнодействующая активного давления грунта на сооружение, составляющая собственного веса элементарных грунтовых призм в направлении предполагаемой поверхности скольжения.
Формула для определения коэффициента устойчивости имеет вид
K = |
|
|
|
||
|
M M
Sr |
= |
|
|
Sa |
|
rb |
(P + |
h )tg |
Ii |
cos |
i |
+ |
|
(C |
Ii |
/ cos |
) |
|||||
|
i |
Ii i |
|
|
|
|
|
|
|
i |
|
|||||
|
E |
l |
+ F a + rb |
|
|
Ii |
h sin |
i |
|
|||||||
|
m m |
v |
|
|
|
i |
|
|
|
|
||||||
, (9.8)
где MSr и MSa – суммы моментов удерживающих сил и сдвигающих сил относительно центра вращения.
Остальные обозначения видны на расчетной схеме (рис. 9.4). Наиболее ответственным моментом расчета является отыс-
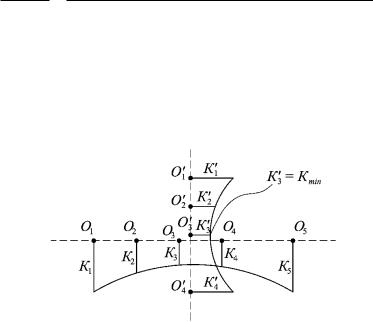
кание наиболее опасной поверхности скольжения (рис. 9.5).
Рис. 9.5. Схема к определению центра вращения наиболее опасной поверхности скольжения
В окрестности предполагаемого центра вращения (рис. 9.5) проводят горизонтальную линию. На этой линии отмечают не-
120
