Электричество и магнетизм / Экзамен / Ответы теория

1.

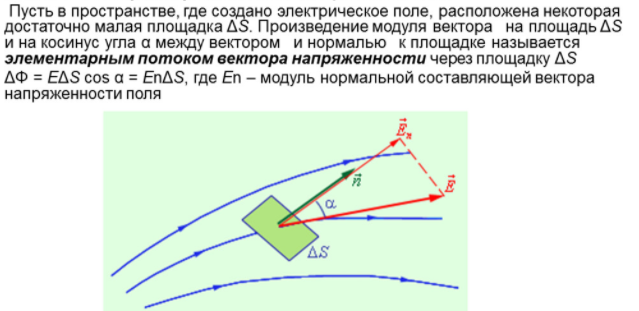
Физическая величина, которая описывает электрическое поле, называется напряженностью электрического поля и обозначается

2.

3.

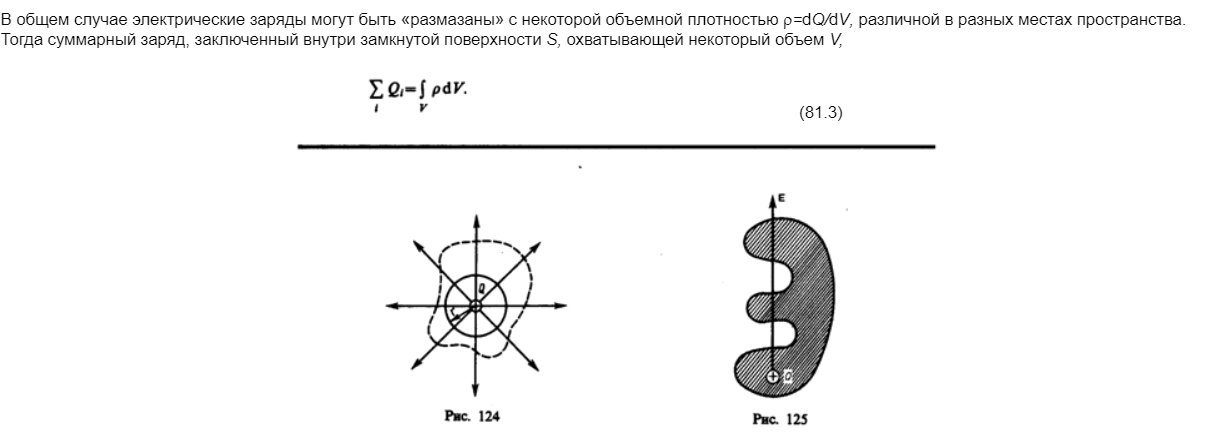
Этот результат справедлив для замкнутой поверхности любой формы. Действительно, если окружить сферу (рис. 124) произвольной замкнутой поверхностью, то каждая линия напряженности, пронизывающая сферу, пройдет и сквозь эту поверхность.

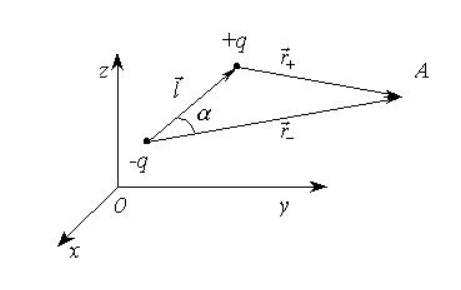
4.  Рассмотрим систему двух точечных электрических зарядов   и  , произвольным образом расположенных в пространстве на расстоянии   друг от друга. Такую систему зарядов назовем  электрическим диполем

Электрическим моментом диполя (дипольным моментом) назовем физическую величину

http://fn.bmstu.ru/data-physics/library/physbook/tom3/ch2/texthtml/ch2_1.htm

5.

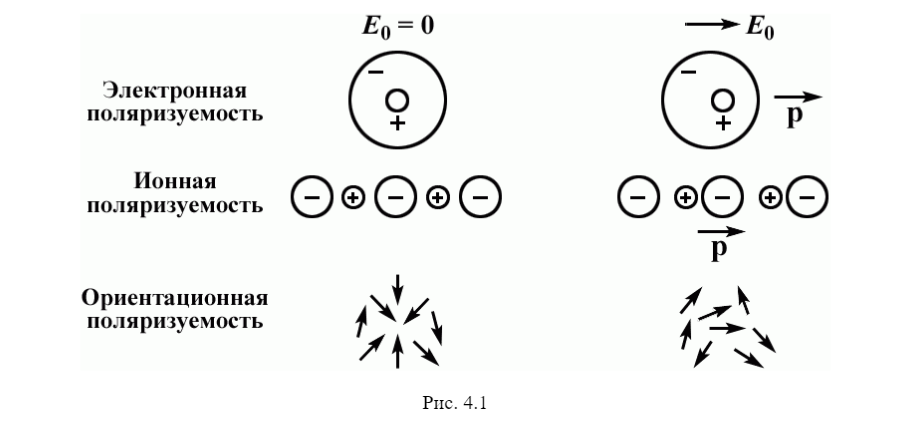
 Электронная поляризуемость обусловлена смещением электронной оболочки атома относительно ядра. Ионная поляризуемость вызвана смещением заряженных ионов по отношению к другим ионам. Ориентационная (дипольная) поляризуемость возникает, когда вещество состоит из молекул, обладающих постоянными электрическими дипольными моментами, которые могут более или менее свободно изменять свою ориентацию во внешнем электрическом поле.

      Есть и другие виды поляризации. Главное в поляризации – смещение зарядов в электростатическом поле. В результате, каждая молекула или атом образует электрический момент p (рис. 4.2):

  Внутри диэлектрика электрические заряды диполей компенсируют друг друга. Но на внешних поверхностях диэлектрика, прилегающих к электродам, появляются заряды противоположного знака (поверхностно связанные заряды).

      Обозначим   – электростатическое поле связанных зарядов. Оно направлено всегда против внешнего поля  . Следовательно, результирующее электростатическое поле внутри диэлектрика

http://ens.tpu.ru/POSOBIE_FIS_KUSN/Электростатика.%20Постоянный%20Ток/04-1.htm

6.

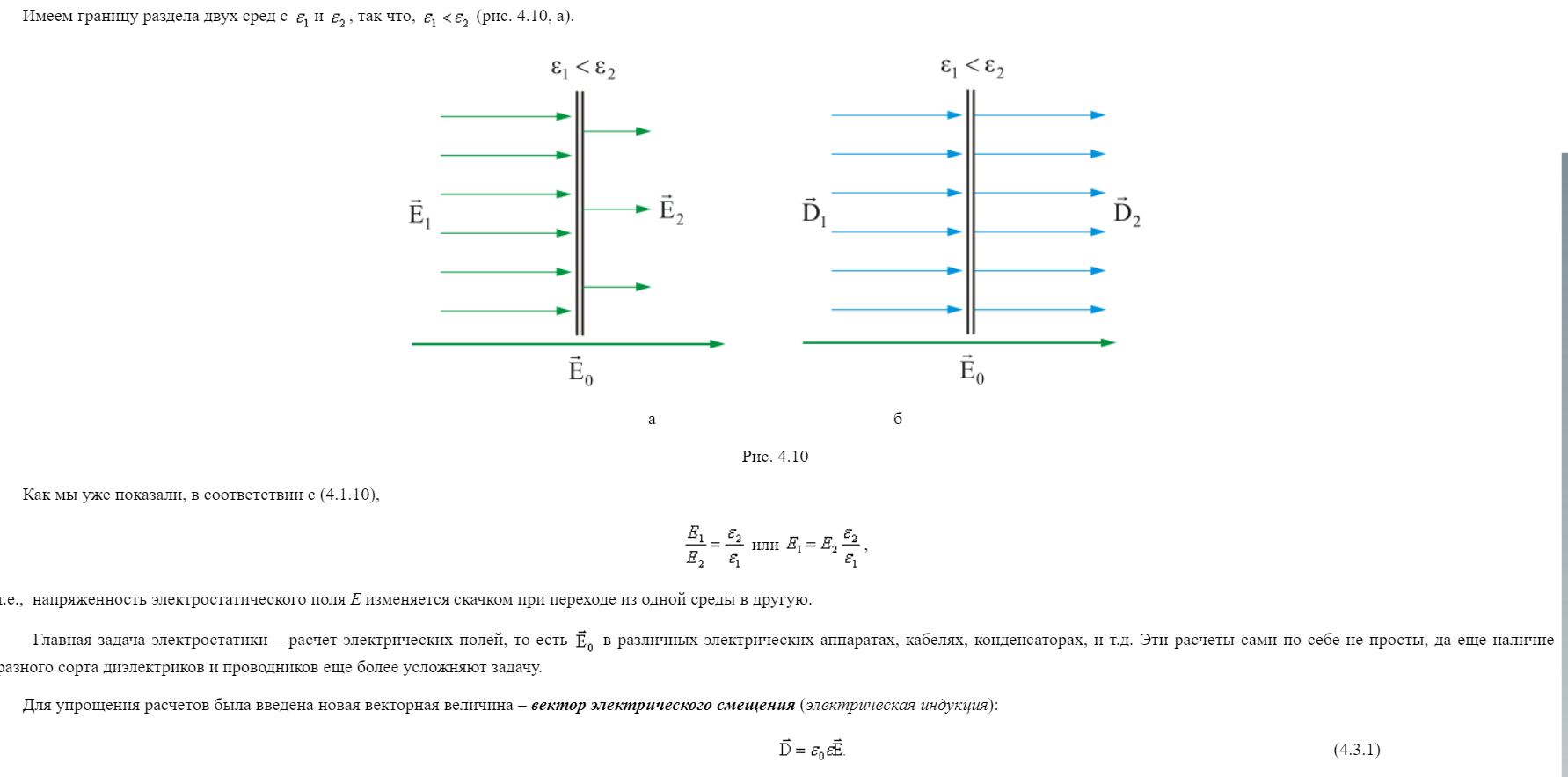
7. http://alexandr4784.narod.ru/Detlaf_2/Detlaf_2_gl6_3.pdf

8.

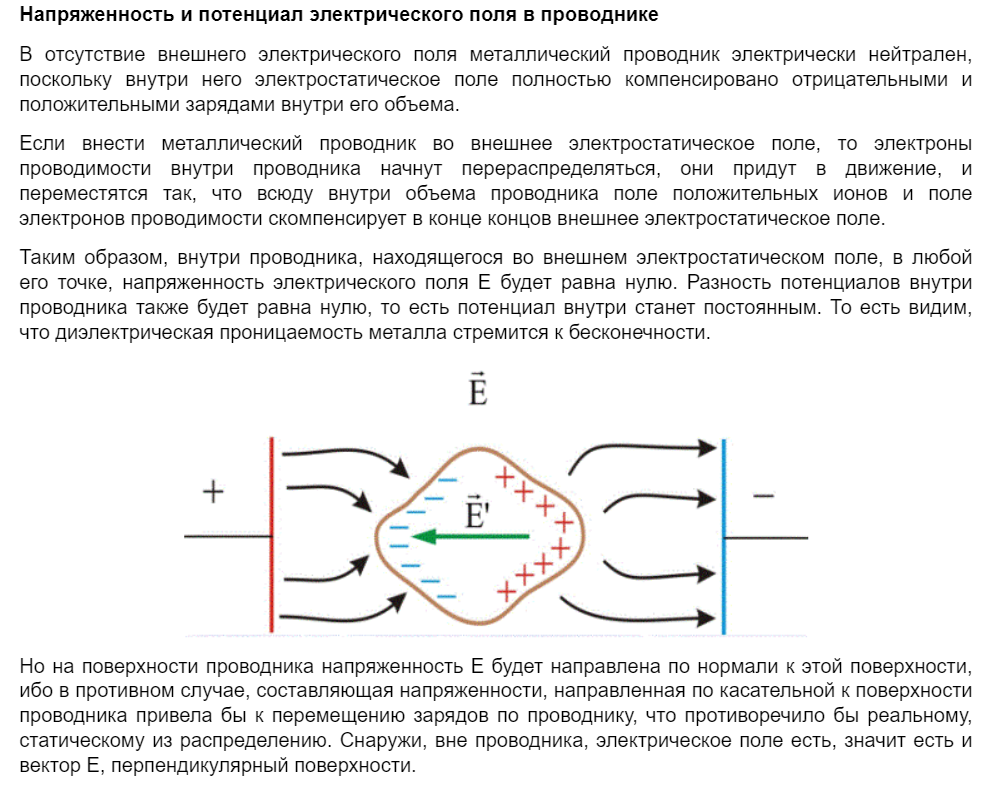
9. https://tsput.ru/res/fizika/1/KR_ELEC/l9.htm

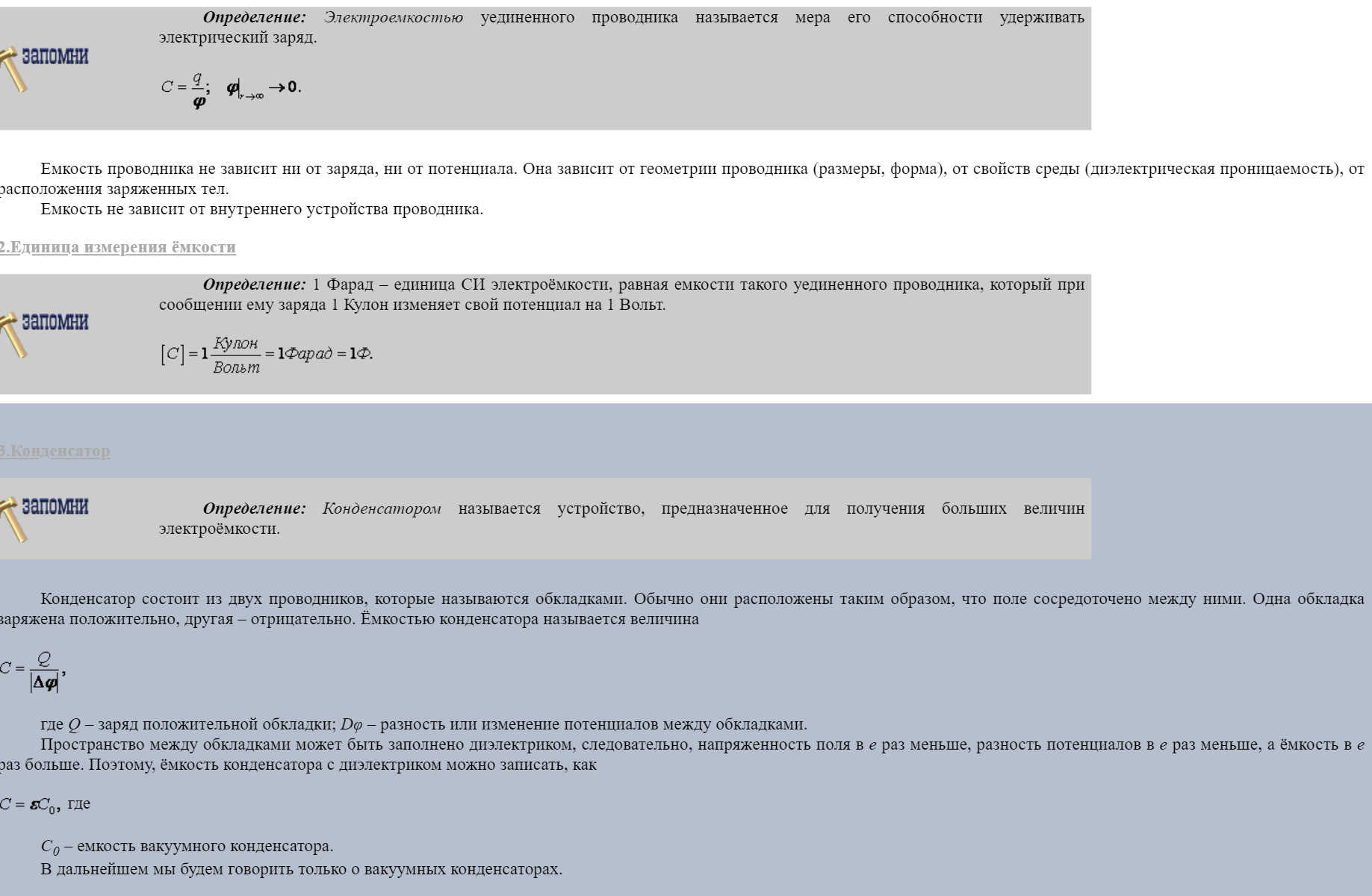
10.

Примеры http://ancient.hydro.nsc.ru/ephys/examples/eldyn/eldyn.html

https://planshet-info.ru/kompjutery/jenergija-polja-sfery-poverhnost-kotoroj#6

https://online.mephi.ru/courses/physics/electricity/data/course/2/2.10.html (лучший)

11.

: сила тока в проводнике прямо пропорциональна напряжению на его концах (разности потенциалов) и обратно пропорциональна сопротивлению этого проводника.

Формула закона Ома записывается в следующем виде:

12.

13.

14. https://online.mephi.ru/courses/physics/electricity/data/course/6/6.3.html

https://electrophysic.ru/elektricheskiy-tok/magnitnyiy-moment-vitka.-opredelenie.-formula.-opyit.html

https://online.mephi.ru/courses/physics/electricity/data/course/5/5.7.html

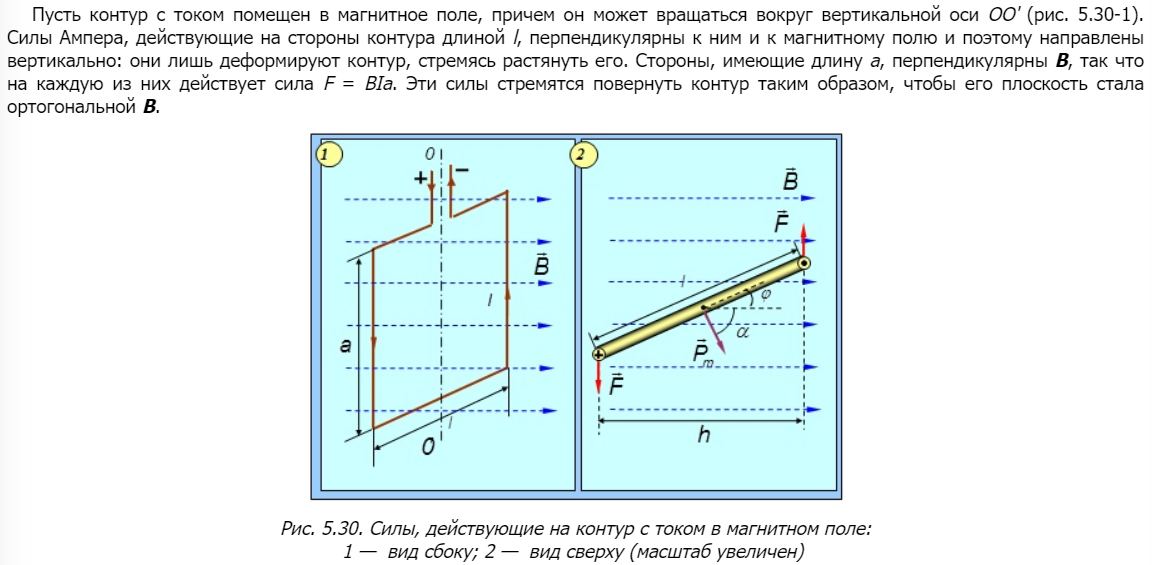
15.

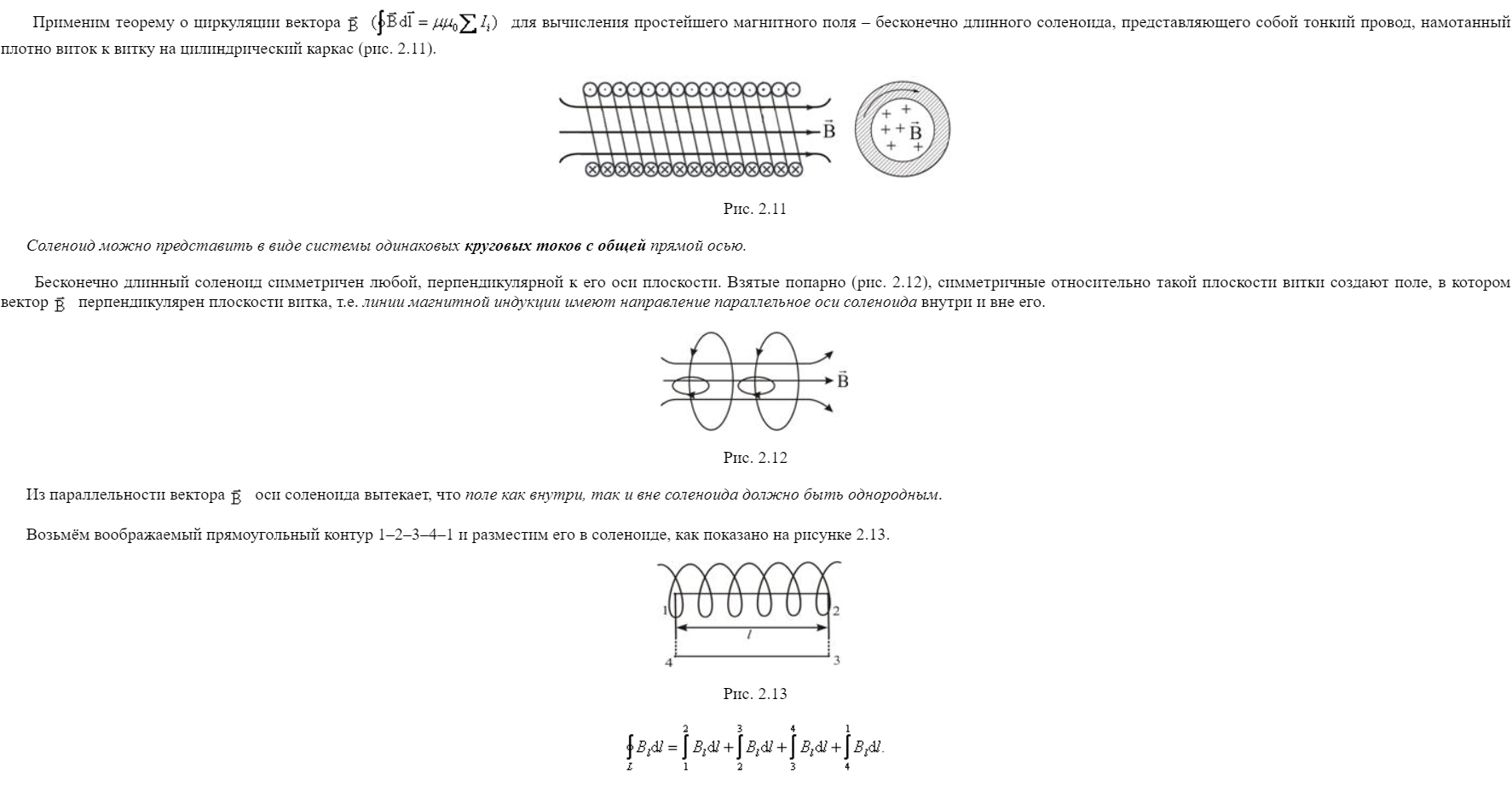
http://ens.tpu.ru/POSOBIE_FIS_KUSN/электромагнетизм/02-7.htm

16.

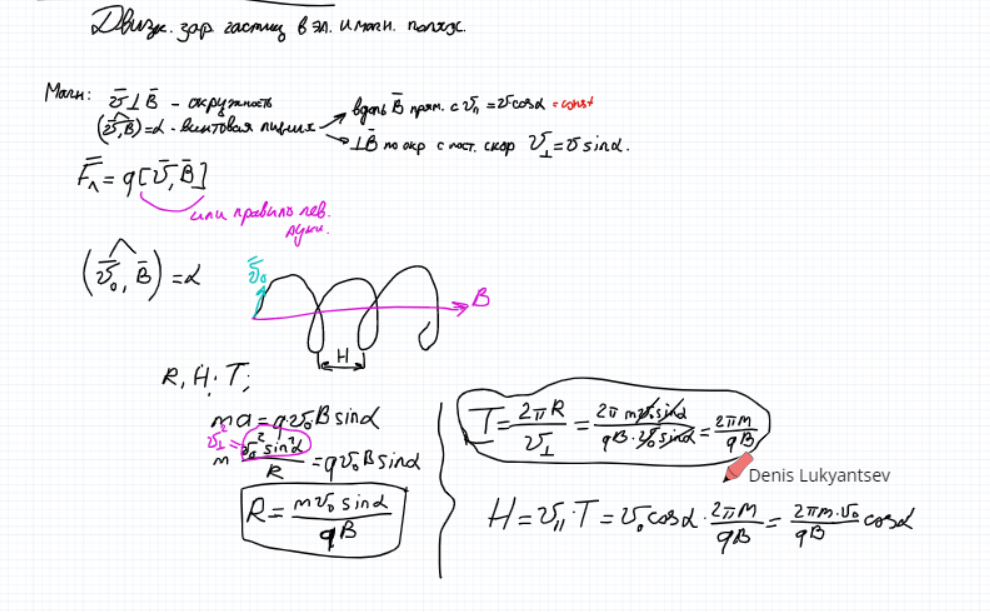
Эффе́кт Хо́лла — явление возникновения поперечной разности потенциалов (называемой также холловским напряжением) при помещении проводника с постоянным током в магнитное поле.

17.

18.

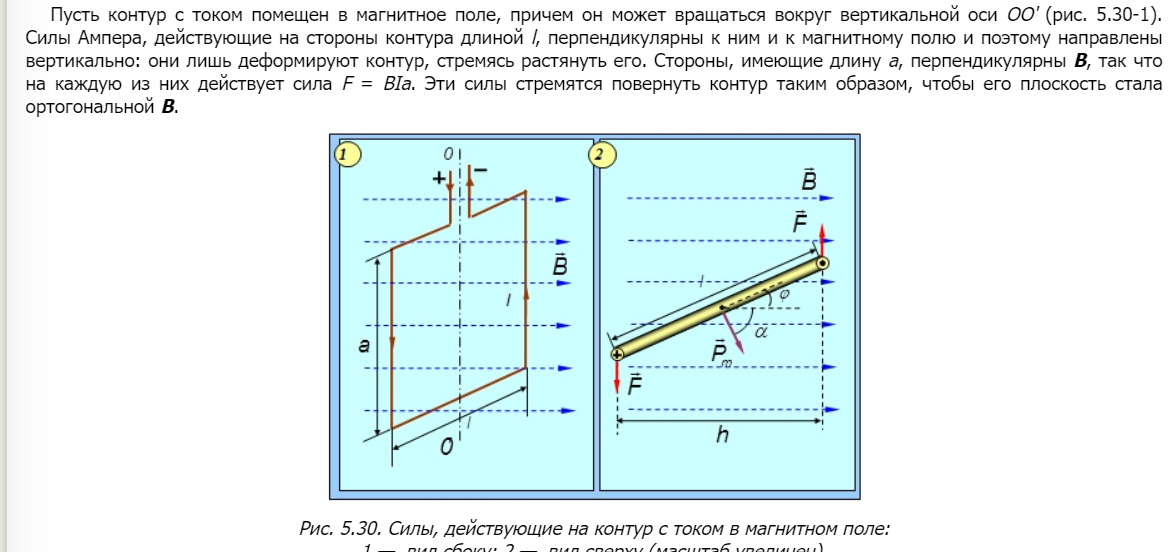
https://online.mephi.ru/courses/physics/electricity/data/course/5/5.7.html

19.

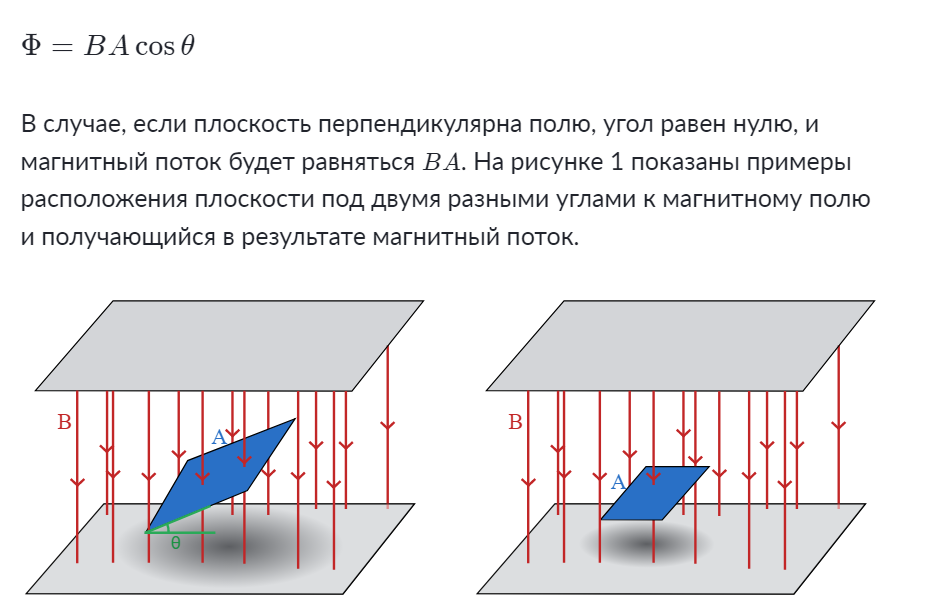
20.

Явление электромагнитной индукции определяется возникновением электрического тока в замкнутом электропроводящем контуре при изменении магнитного потока через площадь этого контура.

Основной закон Фарадея заключается в том, что электродвижущая сила (ЭДС) прямо пропорциональна скорости изменения магнитного потока.

Формула закона электромагнитной индукции Фарадея выглядит следующим образом:

И если сама формула, исходя из вышесказанных объяснений не порождает вопросов, то знак «-» может вызвать сомнения. Оказывается существует правило Ленца – русского ученого, который проводил свои исследования, основываясь на постулатах Фарадея. По Ленцу знак «-» указывает на направление возникающей ЭДС, т.е. индукционный ток направлен так, что магнитный поток, который он создает, через площадь, ограниченную контуром, стремится препятствовать тому изменению потока, которое вызывает данный ток.

21.

22.

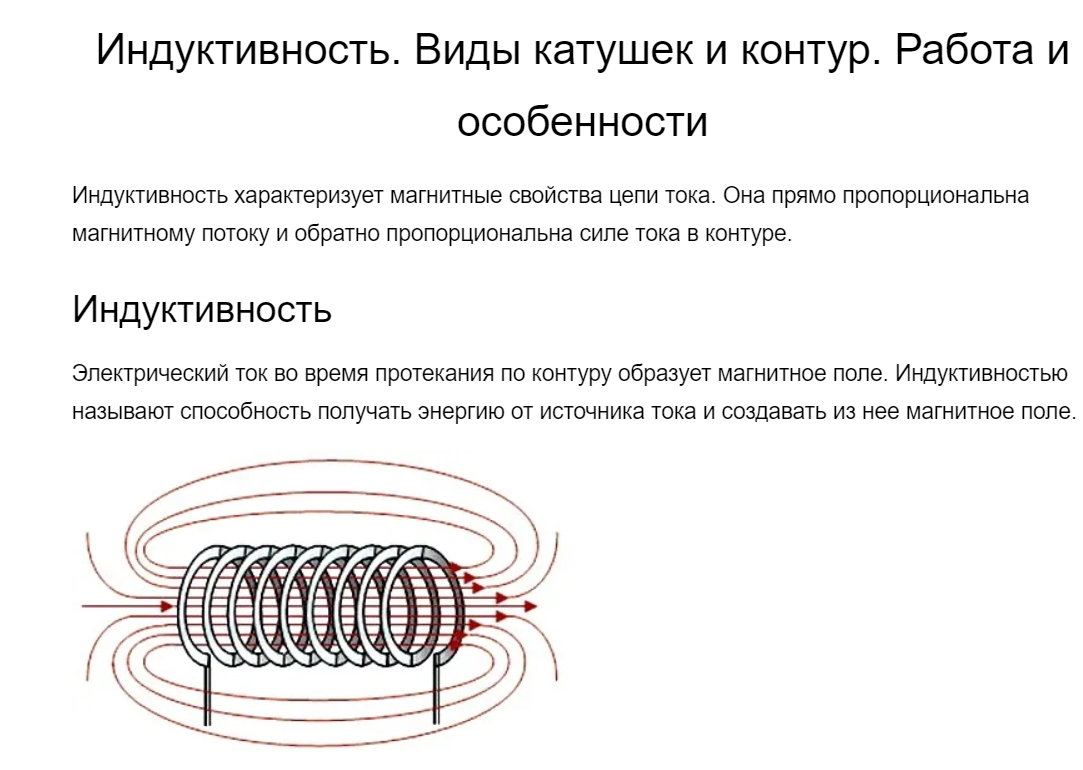
https://mipt.ru/education/chair/physics/kmf/mPh_5/f_5tlro8/f_5tlrv7.pdf

https://studfile.net/preview/3160904/page:3/

23.

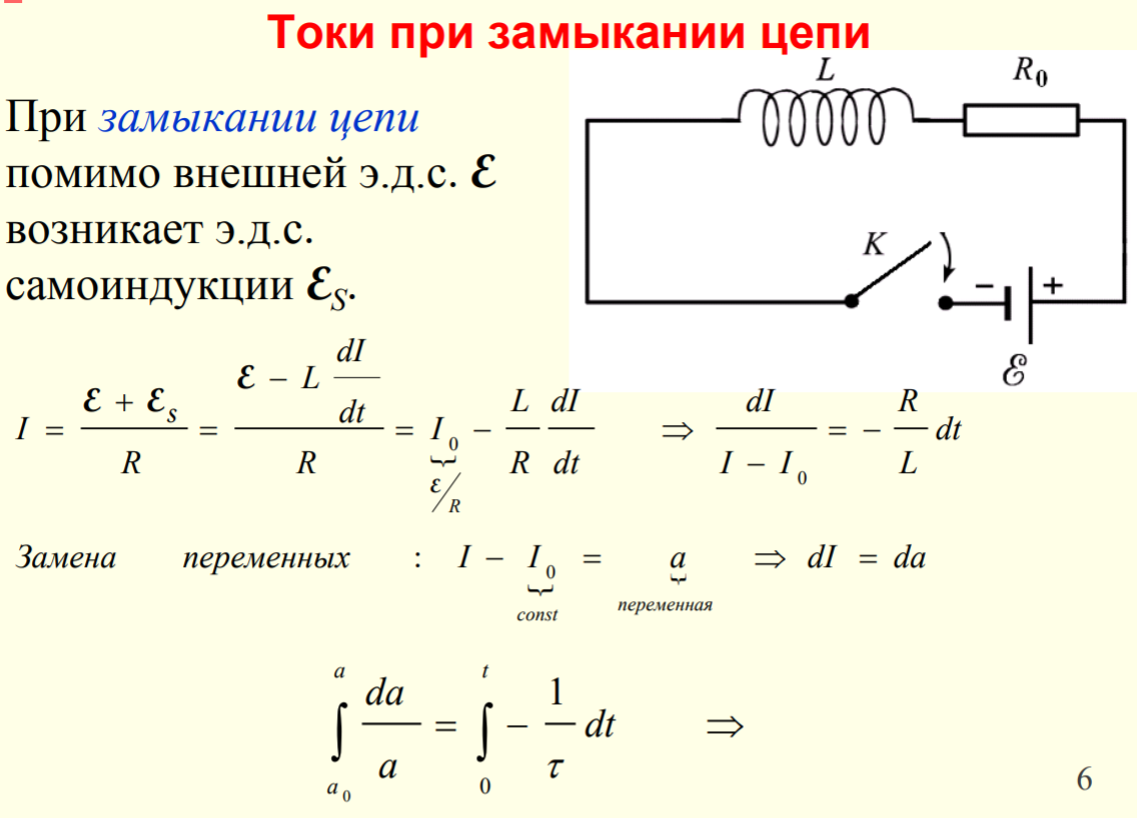
24.

http://ens.tpu.ru/POSOBIE_FIS_KUSN/электромагнетизм/05-5.htm

https://poznayka.org/s29852t1.html

25.

 Намагниченность изотропной среды с напряженностью    связаны соотношением:

,

(6.3.8)

где    – коэффициент пропорциональности, характеризующий магнитные свойства вещества и называемый магнитной восприимчивостью среды. Он связан с магнитной проницаемостью соотношением   .

https://zaochnik.com/spravochnik/fizika/magnitnoe-pole/klassifikatsija-magnetikov/

26.

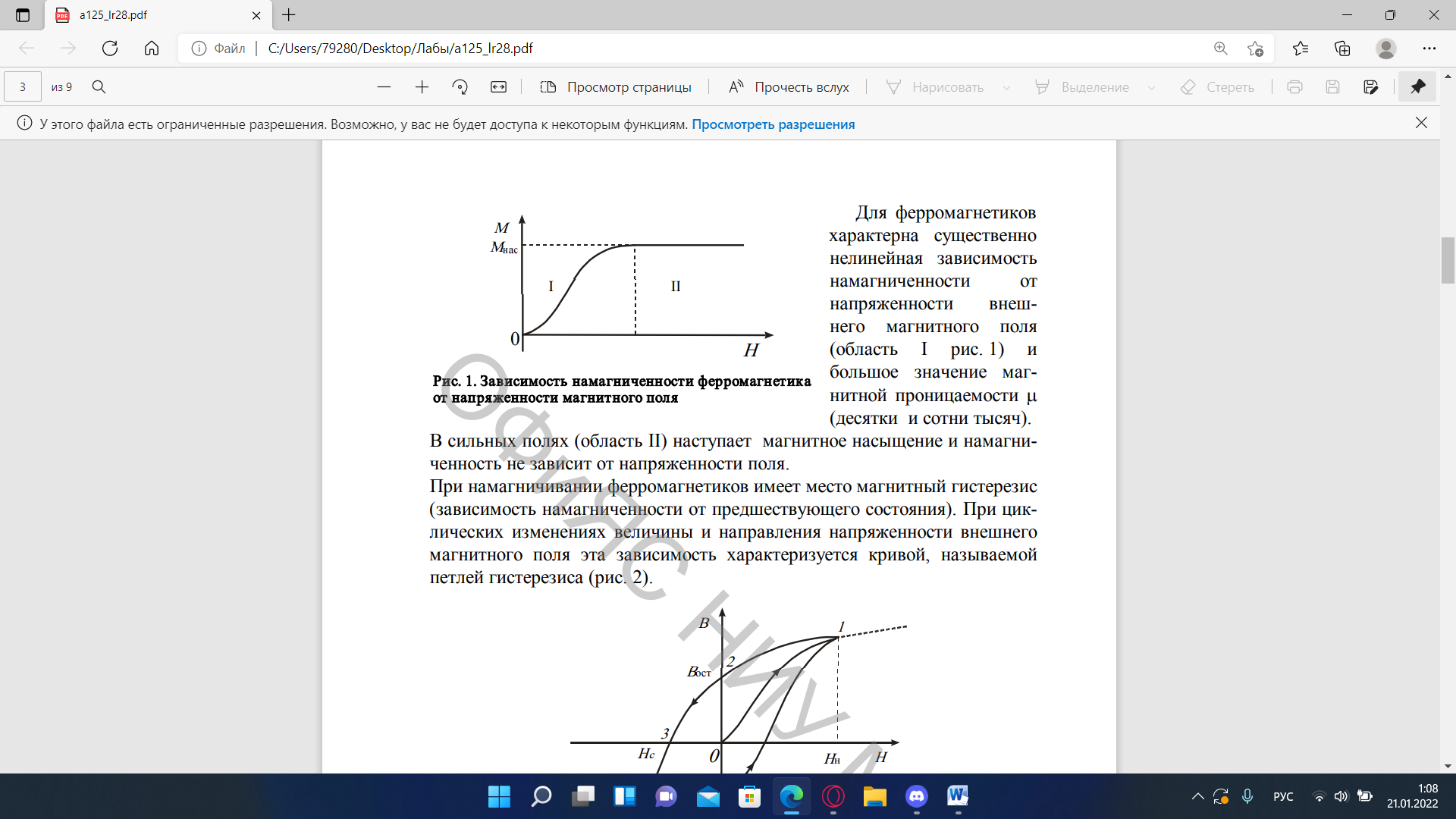
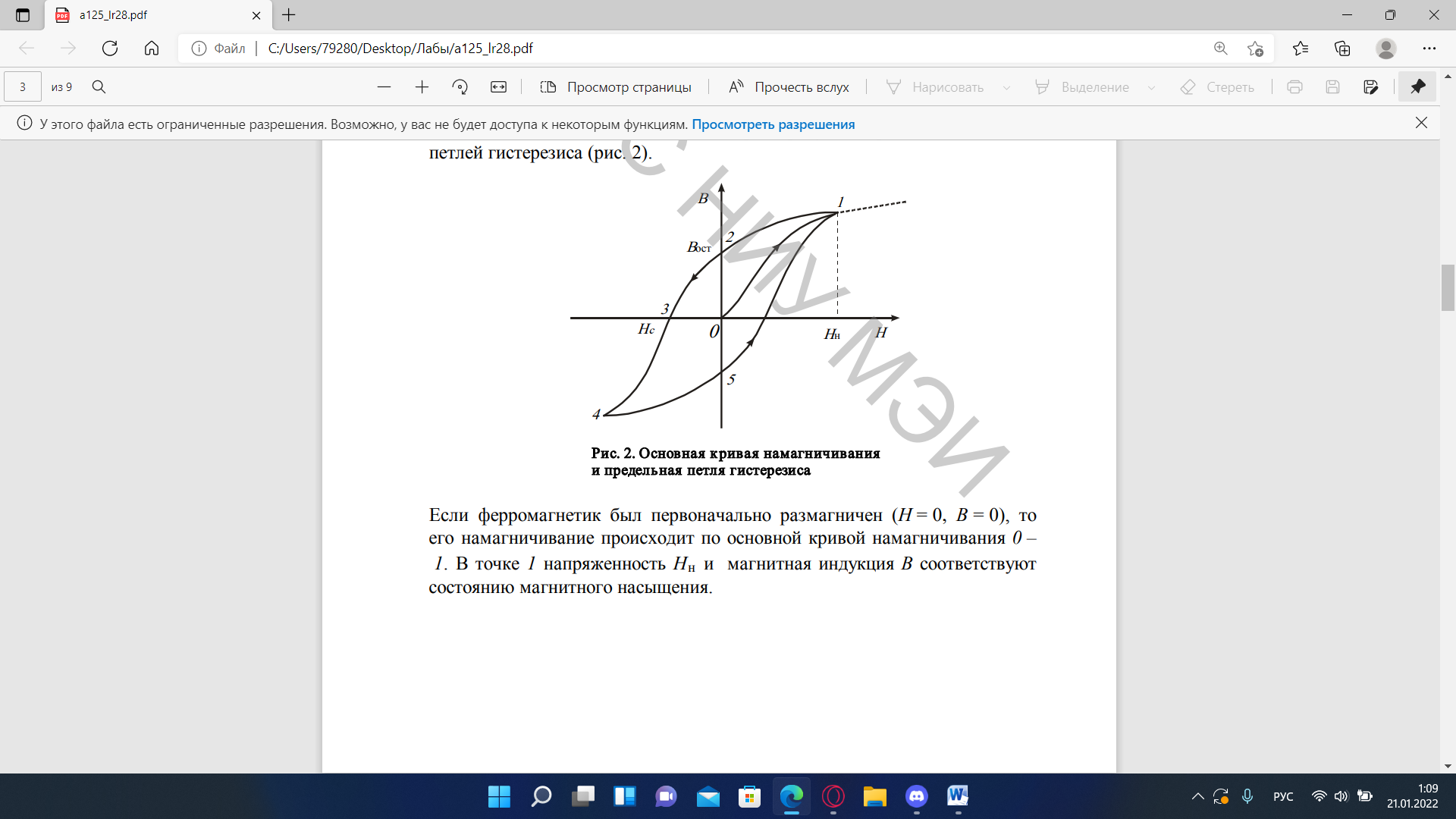
Ферромагнитные свойства вещества проявляются лишь при температурах ниже точки Кюри.

27.лаба

28. https://naparah.com/elektrodinamika/0930458.html

По ссылке доказательства и вывод из формул

29.

В контуре действует только одна э. д.с. – э. д.с. самоиндукции, следовательно

,

где  – падение напряжения на конденсаторе;

– мгновенное значение заряда на обкладках конденсатора;

.

Так как  ,  , то дифференциальное уравнение свободных незатухающих электромагнитных колебаний может быть записано в виде

,

,

Введем обозначение:

где   – собственная циклическая частота контура.

Уравнение колебаний принимает вид

и называется уравнением свободных незатухающих электромагнитных колебаний в дифференциальной форме.

Из математики известно, что решение этого уравнения имеет вид

,

т. е. соответствует формуле (7) и рис. 4 (при  ).

Таким образом, свободные незатухающие электромагнитные колебания являются гармоническими, а их период определяется формулой Томсона:

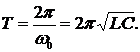
https://pandia.ru/text/80/142/13117.php

https://studme.org/143394/matematika_himiya_fizik/svobodnye_garmonicheskie_kolebaniya_kolebatelnom_konture

30. http://ens.tpu.ru/POSOBIE_FIS_KUSN/Колебания%20и%20волны.%20Геометрическая%20и%20волновая%20оптика/04-3.htm

https://www.chem-astu.ru/chair/study/physics-part1/?p=130

31.

http://electricalschool.info/spravochnik/electroteh/1860-primenenie-rezonansa-naprjazhenijj-i.html

32. https://physics.ru/courses/op25part2/content/chapter2/section/paragraph3/theory.html#.Yen1FL1By3A

https://zaochnik.com/spravochnik/fizika/elektromagnitnye-kolebanija-volny/vynuzhdennye-kolebanija-peremennyj-tok/

33. Подробнее: https://zaochnik.ru/blog/uravneniya-maksvella-bolshe-chem-prosto-uravneniya/

Электромагнитное поле, особая форма материи, посредством которой осуществляется взаимодействие между электрически заряженными частицами (см. Поля физические). Э. п. в вакууме характеризуется вектором напряжённости электрического поля Е и магнитной индукцией В, которые определяют силы, действующие со стороны поля на неподвижные и движущиеся заряженные частицы. Наряду с векторами Е и В, измеряемыми непосредственно, Э. п. может характеризоваться скалярным  и векторным А потенциалами, которые определяются неоднозначно, с точностью до градиентного преобразования (см. Потенциалы электромагнитного поля). В среде Э. п. характеризуется дополнительно двумя вспомогательными величинами: напряжённостью магнитного поля Н и электрической индукцией D (см. Индукция электрическая и магнитная).

  Поведение Э. п. изучает классическая электродинамика, в произвольной среде оно описывается Максвелла уравнениями, позволяющими определить поля в зависимости от распределения зарядов и токов. Микроскопические Э. п., созданные отд. элементарными частицами, характеризуются напряжённостями микроскопических полей: электрического поля е и магнитного h. Их средние значения связаны с макроскопическими характеристиками Э. п. следующим образом:  ,  . Микроскопические поля удовлетворяют Лоренца — Максвелла уравнениям.

  Э. п. неподвижных или равномерно движущихся заряженных частиц неразрывно связано с этими частицами; при ускоренном движении частиц Э. п. «отрывается» от них и существует независимо в форме электромагнитных волн.

  Порождение Э. п. переменным магнитным полем и магнитного поля — переменным электрическим приводит к тому, что электрические и магнитные поля не существуют обособленно, независимо друг от друга. Компоненты векторов, характеризующих Э. п., образуют, согласно относительности теории, единую физ. величину — тензор Э. п., компоненты которого преобразуются при переходе от одной инерциальной системы отсчёта к другой в соответствии с Лоренца преобразованиями.

  При больших частотах Э. п. становятся существенными его квантовые (дискретные) свойства. В этом случае классическая электродинамика неприменима и Э. п. описывается квантовой электродинамикой.

 

34.

Волна – это процесс распространения колебаний в пространстве с течением времени. Так как колебания распространяются в пространстве с течением времени, то в уравнении волны необходимо также учесть пространственные координаты и время. Уравнение волны A(z,t) имеет вид

, (3.2)

Примеры: https://www.webmath.ru/poleznoe/fizika/fizika_157_vektor_pojntinga.php