
- •Московский энергетический институт
- •Физический эксперимент. Статистическая обработка результатов физического эксперимента
- •ФИЗИЧЕСКИЕ ИЗМЕРЕНИЯ
- •ФИЗИЧЕСКИЕ ИЗМЕРЕНИЯ
- •ФИЗИЧЕСКИЕ ИЗМЕРЕНИЯ
- •ФИЗИЧЕСКИЕ ИЗМЕРЕНИЯ
- •ПОГРЕШНОСТЬ ИЗМЕРЕНИЯ
- •ПОГРЕШНОСТЬ ИЗМЕРЕНИЯ
- •КЛАССИФИКАЦИЯ ПОГРЕШНОСТЕЙ
- •Классификация погрешностей по форме числового выражения
- •Классификация погрешностей по характеру проявления в эксперименте
- •Классификация погрешностей по источнику появления
- •ПОГРЕШНОСТЬ ПРЯМОГО ИЗМЕРЕНИЯ
- •ПОГРЕШНОСТЬ ПРЯМОГО ИЗМЕРЕНИЯ
- •ПОГРЕШНОСТЬ ПРЯМОГО ИЗМЕРЕНИЯ
- •ПОГРЕШНОСТЬ ПРЯМОГО ИЗМЕРЕНИЯ
- •ПОГРЕШНОСТЬ ПРЯМОГО ИЗМЕРЕНИЯ
- •ПОГРЕШНОСТЬ ПРЯМОГО ИЗМЕРЕНИЯ
- •ПОГРЕШНОСТЬ ПРЯМОГО ИЗМЕРЕНИЯ
- •ПОГРЕШНОСТЬ ПРЯМОГО ИЗМЕРЕНИЯ
- •ПОГРЕШНОСТЬ КОСВЕННОГО ИЗМЕРЕНИЯ
- •ПОГРЕШНОСТЬ КОСВЕННОГО ИЗМЕРЕНИЯ
- •ПОГРЕШНОСТЬ КОСВЕННОГО ИЗМЕРЕНИЯ
- •Учет погрешностей трансцендентных и иррациональных величин
- •Учет погрешностей трансцендентных и иррациональных величин
- •Учет погрешностей физических постоянных, табличных значений, данных установок
- •ПРИМЕР ИЗМЕРЕНИЙ И СТАТИСТИЧЕСКОЙ ОБРАБОТКИ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
- •Измерим высоту цилиндра пять раз с помощью штангенциркуля. Результаты измерений запишем в табл.2.
- •Прямое измерение высоты цилиндра
- •Прямое измерение высоты цилиндра
- •Прямое измерение высоты цилиндра
- •Прямое измерение высоты цилиндра
- •Статистическая обработка результатов измерения
- •Статистическая обработка результатов измерения
- •Статистическая обработка результатов измерения
- •Статистическая обработка результатов измерения
- •Правила округления результатов измерений
- •Правила округления результатов измерений
- •Запись окончательного результата измерений
- •Описания лабораторных работ размещены на сайте кафедры Общей физики и ядерного синтеза по

ПОГРЕШНОСТЬ КОСВЕННОГО ИЗМЕРЕНИЯ
При косвенном измерении искомое значение физической величины рассчитывают используя известную зависимость (формулу) между этой величиной и другими величинами, определяемыми путем прямых измерений.
В формулу кроме результатов прямых измерений могут входить также физические постоянные, табличные значения и данные экспериментальной установки.
Пусть при косвенном измерении искомое значение физической величины y находят из соотношения y = f(x1, x2, x3 ,...), где x1, x2, …xi – значения
физических величин, найденные в результате прямых измерений, или заданные как данные установки.
Абсолютная погрешность косвенного измерения определяется по формуле
|
|
y |
2 |
|
2 |
... |
|
|
y |
|
2 |
2 |
... , |
|||
y |
|
|
x1 |
|
|
|
|
xi |
|
|||||||
x |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
x |
i |
|
|
|
||||
|
1 |
|
|
|
|
|
|
|
|
|
||||||
где xi – погрешности прямых измерений; |
|
y |
|
частные производные. |
||||||||||||
|
xi |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

ПОГРЕШНОСТЬ КОСВЕННОГО ИЗМЕРЕНИЯ
Если искомая величина определяется суммой
y a1 x1 a2 x2 ... ,
то в этом случае удобно вывести формулу для абсолютной погрешности
y 
 a12 x1 2 a22 x2 2 ... .
a12 x1 2 a22 x2 2 ... .
Пример:
y 2x1 3x2 ,
y 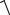
 22 x1 2 32 x2 2 .
22 x1 2 32 x2 2 .

ПОГРЕШНОСТЬ КОСВЕННОГО ИЗМЕРЕНИЯ
Если искомая величина определяется произведением степенных функций
y x1 1 x2 2 ... ,
то в этом случае удобно сначала вывести формулу и вычислить относительную погрешность
|
y |
|
|
|
|
|
, |
y |
|
12 x |
2 22 x |
|
2 ... |
||
|
y |
|
1 |
|
2 |
|
|
|
|
|
|
|
|
и затем абсолютную погрешность
y y y .
Пример:
y x12 x23 x30,5 ,
y yy 
 22 x1 2 32 x2 2 0,5 2 x3 2 .
22 x1 2 32 x2 2 0,5 2 x3 2 .

Учет погрешностей трансцендентных и иррациональных величин
Трансцендентные и иррациональные величины, физические постоянные, как правило, определены весьма точно. Например π = 3,14159…, число Авогадро NА = (6,0220921 ± 0,0000062)·1023 1/моль, ускорение свободного
падения на широте Москвы g = (9,80655 ± 0,00005) м/с2.
Обычно в расчетную формулу подставляют округленные значения таких величин:
3,14 |
g 9,81 м / c2 . |
Если при этом взять на одну значащую цифру больше, чем число значащих цифр в результатах прямых измерений, то относительная погрешность округления будет заведомо много меньше относительной погрешности прямых измерений. В таком случае данное число можно считать точным и его погрешностью пренебречь.

Учет погрешностей трансцендентных и иррациональных величин
Пример. Пусть вычисляется площадь круга по формуле S = r2. Формула для определения относительной погрешности имеет вид
S |
|
2 |
|
r |
2 |
|
||
|
|
|
4 |
r |
. |
|||
|
|
|
|
|
|
|
||
В результате прямых измерений получено значение радиуса
r = (1,35 0,03) см.
Если взять = 3,142 , то относительная погрешность округления числа будет на два порядка меньше относительной погрешности измерения радиуса:
δ |
0,0005 |
0,00013, |
|
r |
|
0,03 |
0,022 . |
|
|
||||||
π |
3,142 |
|
|
1,35 |
|
||
|
|
|
|
|
|||
В этом случае число можно считать точным и относительную погрешность площади рассчитать по формуле
S |
|
2 |
|
r 2 |
2 |
r |
. |
||
|
|
|
4 |
r |
|
r |
|||
|
|
|
|
|
|
|
|||

Учет погрешностей физических постоянных, табличных значений, данных установок
Погрешность табличных данных и данных установок принимается равной половине единицы последнего разряда значения, приведенного в таблице или на установке.
1 2 3 4 5 6 7 8 9 0 – это цифры.
65,32 |
это число. |
Число состоит из знака, цифр и разделителя. |
|
разряд сотых |
|
|
разряд десятых |
|
|
разряд единиц |
|
|
разряд десятков |
|
Половина единицы разряда сотых – 0,005
т = 123,4 г |
0,1 |
m = ±0,05 г |
|
2 |
|||
|
|
||
l = 123 мм |
1 |
l = ± 0,5 мм |
|
2 |
|||
|
|
||
= 123,02 с |
0,01 |
τ = ± 0,005 с |
|
2 |
|||
|
|

ПРИМЕР ИЗМЕРЕНИЙ И СТАТИСТИЧЕСКОЙ ОБРАБОТКИ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
Необходимо определить объем цилиндра радиусом R и высотой h.
|
|
|
|
Радиус цилиндра задан R = 18 мм. |
|
R |
|
Высота цилиндра h определяется путем прямого |
|
|
|
|||
|
|
|||
|
|
|||
|
|
|||
|
|
|
|
измерения. Измерения проводятся штангенциркулем с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ценой деления нониуса 0,1 мм. |
|
|
|
|
|
hОбъем рассчитываем по формуле:
V R2h.
Таблица 1. Спецификация измерительных приборов
Название |
|
Пределы |
|
Цена |
|
Предел допускаемой |
|
|
|
инструментальной |
|||
прибора и его тип |
|
измерения |
деления |
|
||
|
|
погрешности |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Штангенциркуль |
|
0 -150 мм |
|
0,1 мм |
|
0,1 мм |
|
|
|
|
|
|
|
|
|
Данные установки: |
|
|||
|
R = 18 мм; |
R = ± 0,5 мм. |
|
|||

Измерим высоту цилиндра пять раз с помощью штангенциркуля. Результаты измерений запишем в табл.2.
Таблица 2. Измерение высоты образующей цилиндра
№h, мм

Прямое измерение высоты цилиндра
№ h, мм
1 12,3

Прямое измерение высоты цилиндра
№ h, мм
1 12,3
2 12,1
