

Лекция 5
Применение теории подобия в расчетах и проектировании насосов.
Пересчет характеристик насосов.
Коэффициент быстроходности насосов.
Связь характеристик насосов с коэффициентом быстроходности.
Работа насоса в системе.
Рабочая точка.
Совместная работа нескольких насосов на общую сеть.
Применение теории подобия в расчетах и проектировании насосов.
На практике часто возникают задачи, связанные с расчетом характеристик насоса при скорости вращения колеса насоса, отличной от приведенной в паспорте.
Другой тип задач связан с определением скорости вращения колеса наноса, отвечающей оптимальным значениям подачи и напора.
При проектировании насосов часто идут от модели к реальному насосу. Поэтому возникает необходимость
пересчета характеристик модельного насоса на характеристики реального.
Во всех этих случаях используются элементы теории подобия: геометрического, кинематического, динамического.
Геометрическое подобие: все размеры одного насоса пропорциональны размерам другого.
Кинематическое подобие: все скорости в любой точке потока изменяются в одно и то же число раз, а направления скоростей остаются прежними.
Динамическое подобие: подобие сил вязкости. При соблюдении его потери и напор при турбулентном течении пропорциональны квадрату скорости.

Влияние изменения скорости вращения колеса насоса на подачу, напор и мощность (кинематическое подобие).
1) Пусть известно значение подачи Q при скорости вращения колеса насоса n. Нужно определить подачу Q’ при скорости вращения колеса насоса n’. Допустим n’ › n.
При увеличении скорости вращения колеса насоса n увеличивается пропорционально и окружная скорость u2, т.к. u2 = π d2 n. При выполнении кинематического подобия в такое число раз увеличатся и скорости С2, W2.
С другой стороны по уравнению неразрывности Q=ρ С F,
где F- площадь (F=const).
Подача Q пропорциональна скорости С и, следовательно, пропорциональна скорости вращения колеса насоса n.
Условие подобия: |
Тогда |
2) Пусть известно значение напора Н при скорости вращения колеса насоса n. Нужно определить напор Н’ при скорости вращения колеса насоса n’. Допустим n’ › n.
Поскольку Н = u2 C2u/g, то напор пропорционален n² .
Условие подобия:  Тогда
Тогда 
3) Пусть известно значение мощности N при скорости вращения колеса насоса n. Нужно определить мощность N’ при скорости вращения колеса насоса n’ . Допустим n’ › n.
Подача Q пропорциональна n, напор Н пропорционален n².
Потребляемая насосом мощность N = ρ g Q H/ηн. Полагают, что КПД насоса ηн остается постоянным.
Условие подобия: |
Тогда |

Влияние изменения геометрических размеров насоса на подачу, напор и мощность (геометрическое подобие).
Рассмотрим, как меняется подача, напор и мощность при изменении размеров насоса (геометрическое подобие) при неизменной скорости вращения колеса насоса n.
1)Пусть известно значение подачи Q для первого насоса. Нужно определить подачу Q’ для насоса геометрически подобного данному. Скорость вращения рабочих колес этих насосов одинакова. Все размеры второго насоса отличаются от размеров первого насоса в λ раз.
(из условия кинематического подобия)
Следовательно
2) Пусть известно значение напора Н для первого насоса. Нужно определить напор Н’ для насоса геометрически подобного данному.
Скорость вращения рабочих колес этих насосов одинакова. Пусть все размеры второго насоса отличаются от размеров первого насоса в λ раз.
(из условия кинематического подобия)
Следовательно
3) Пусть известно значение потребляемой мощности N для первого насоса. Нужно определить потребляемую мощность N’ для насоса геометрически подобного данному. Скорость вращения рабочих колес этих насосов одинакова. Пусть все размеры второго насоса отличаются от размеров первого насоса в λ раз. Потребляемая мощность N = ρ g Q H/ηн. Полагают, что КПД насоса ηн остается постоянным.
Тогда
Объединенные формулы пересчета для геометрически подобных насосов с различными скоростями вращения рабочегоколеса

Коэффициент быстроходности насосов.
Насосы и вентиляторы имеют разнообразие области применения и поэтому отличаются друг от друга по конструктивным и другим признакам. Вполне естественно, что в связи с этим возникает потребность в классификации этих машин не по различным признакам, а по какому – либо одному признаку, который наиболее полно отражал бы их основные свойства, связанные сущностью происходящих в них процессов.
Таким критерием является величина, выражающая зависимость между основными параметрами работы машины. Пусть имеются 2 насоса: модельный и геометрически подобный ему.
Полученные формулы позволяют делать пересчёт характеристик лопаточных машин с точностью, достаточной для критических целей при изменении n и размеров с сохранением геометрического подобия. Такие расчёты имеют высокое значение, т.к. позволяют существенно сократить расходы на получение действительных характеристик.
Особенно большой выигрыш получается при доводке машин на экспериментальных стендах, где натурная машина заменяется моделью. После доводки модели на стенде снимается основная характеристика, которая пересчитывается к нормальным условиям ρ0, к определённым размерам и частоте вращения n.
Параметры насосов:
Коэффициентом быстроходности насоса называется число оборотов колеса насоса, геометрически подобного данному, который при напоре в 1 м и подаче 0,075 м³/с развивает полезную мощность 75 кгcм/с.
На рисунке отображена характеристика насоса для n=var

Коэффициент быстроходности насосов.
Рассмотрим два геометрически подобных насоса. Коэффициент быстроходности насоса
Рассмотрим серию геометрически подобных насосов. Для этой серии ns будет одинаков, т.к. для этой серии существует только 1 насос, который при Nп = 75 кгcм/с и Н = 1 м даёт Q = 0.075 м³/с.
ns≠f(n).
ns для одного и того же насоса есть f(Q).
К.б.н. не определяет однозначно гидродинамическую схему, т.е. насосы различной конфигурации могут иметь одинаковые ns и в этом заключается его недостаток.
Для насоса величина ns отвечает максимуму КПД.
Тем не менее, ns является удобным критерием для классификации насосов, т.к. он выражает зависимость между основными параметрами работы.
ns возрастает, когда возрастает Q , ns уменьшается, когда возрастает Н . Раз Q возрастает, то сечения труб большие. Если Н возрастает, то диаметр колеса d2 должен быть большой. И, наоборот, при малом Н диаметр d2 уменьшается.
ns влияет и на форму и размеры отвода.
Коэффициент быстроходности для вентиляторов также применяется и имеет тот же смысл, но выражается иной численной зависимостью, а именно:

Связь характеристик насосов с коэффициентом быстроходности.
Рабочие колеса насосов разделяют на 5 классов: тихоходные, нормальные, быстроходные, диагональные, осевые.
Возвращаясь к схемам рабочих насосов можем отметить, какие коэффициенты быстроходности соответствуют схеме.
Как видно на схемах, рабочие колёса различных типов отличаются друг от друга отношением диаметров d2/d0 и наклоном входных и выходных кромок.
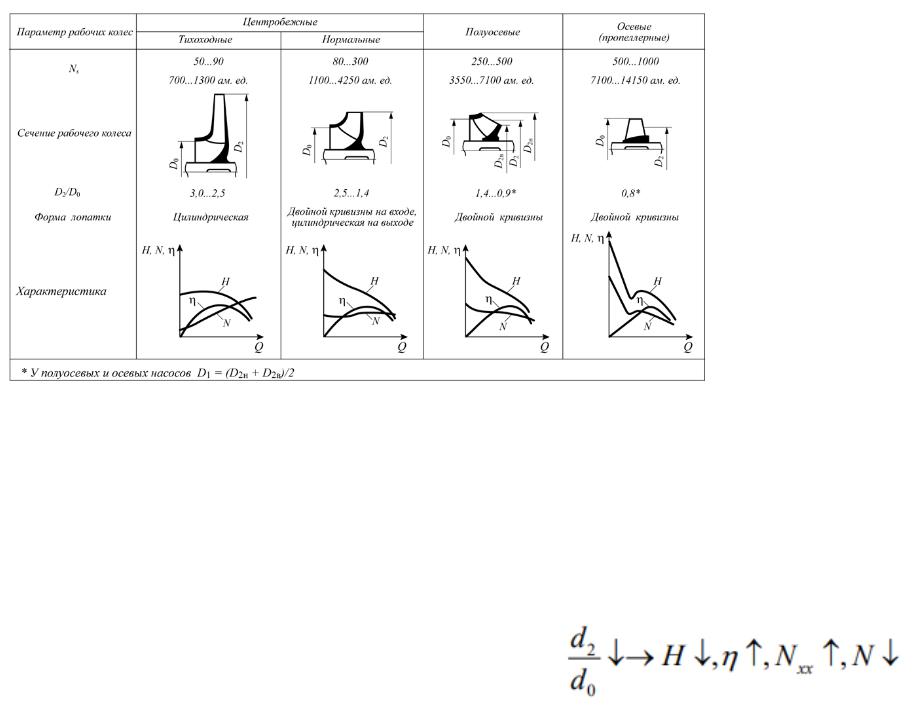
В соответствии с уравнением Эйлера напор растёт с ростом u2 (при u1=const). Поэтому, чем больше отношение d2/d0 при d0=const, тем более высоконапорным является насос. Соответственно при уменьшении d2/d0 входная кромка постепенно поворачивается и форма колеса от радиальной (центробежной) переходит в осевую.
Сравнивая характеристики, мы видим, что расчётные напоры снижаются с уменьшением d2/d0, а производительность и к.п.д. возрастают.
Причём переходным типом колеса является диагональное.
Мощность холостого хода также постепенно возрастает, а расчётная мощность соответственно уменьшается. По аналогии с насосами и вентиляторы разделяют на тихоходные и быстроходные.
По этой классификации:
вентиляторы с лопатками загнутыми вперед называются тихоходными;
срадиальными – нормальными;
слопатками загнутыми назад и осевые – быстроходными.

Работа насоса в системе.
Устройство, состоящее из насоса, электродвигателя, соединительной муфты (или вариатора частоты вращения) и измерительных приборов называется насосной установкой.
На практике, особенно в энергетике, встречается большое число схем насосных установок с разными типами насосов. Однако гидравлическая часть насосной установки, как правило, выполняется по одинаковой схеме.
Насосная установка и сеть трубопроводов составляют единую систему. Рассмотрим схему такой системы.

Работа насоса в системе.
Запишем уравнение Бернулли для сечений 1-1 и 2-2:
где С1 – скорость во всасывающем трубопроводе
Энергия жидкости во всасывающем трубопроводе на входе в насос:
Запишем уравнение Бернулли для сечений 3-3 и 4-4:
где Н2 - энергия жидкости в напорном трубопроводе на выходе из насоса
Напор насоса Н = Н2 - Н1 = :
