

Лекция 4
Кинематика потока в рабочем колесе центробежного насоса.
Законы сохранения: количества движения, энергии, массы.
Определение напора насоса по показаниям приборов.
Теоретические характеристики насоса. Зависимость теоретических характеристик насоса от подачи и угла выхода потока жидкости из рабочего колеса.
Действительные характеристики насосов.
Зависимость действительных характеристик насоса от подачи и угла выхода потока жидкости из рабочего колеса.
Безразмерные характеристики насоса.
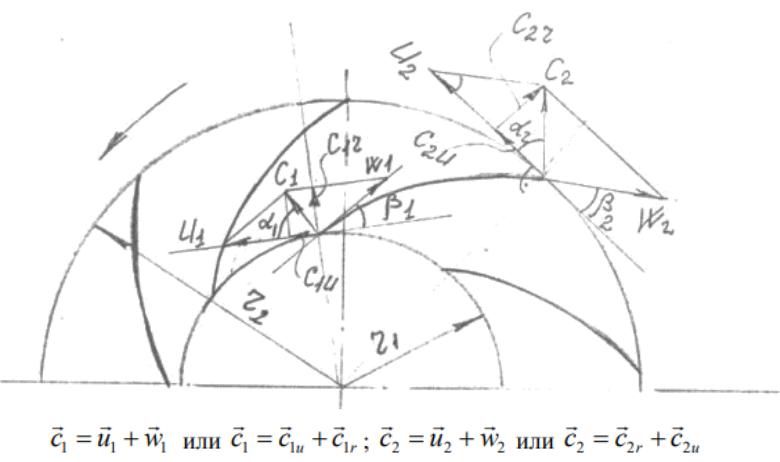
КИНЕМАТИКА ПОТОКА В РАБОЧЕМ КОЛЕСЕ ЦЕНТРОБЕЖНОГО НАСОСА
По мере движения частицы жидкости вдоль лопатки r ↑ U↑ C↑ , т.е. кинетическая энергия также растёт. В то же время, т.к. канал выполняется обычно диффузорным, т.е. расширяющимся, то W ↓, и следовательно, кинетическая энергия частично преобразуется в потенциальную.
Таким образом, при перемещении жидкости через рабочее колесо возрастает как потенциальная, так и кинетическая энергия перемещаемой среды, за счёт взаимодействия её с вращающейся решёткой лопастей рабочего колеса
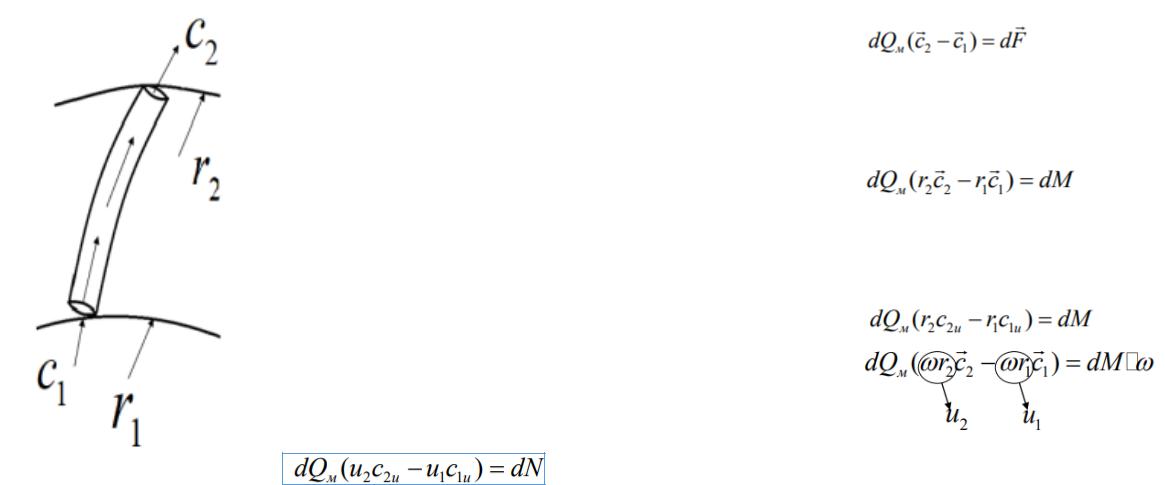
Закон сохранения количества движения. Уравнение Эйлера.
Если не учитывать потери, которые имеют место в насосе, то, в соответствии с законом сохранения энергии, мощность, потребляемая насосом, расходуется на приращение энергии рабочей среды. Для определения этого приращения энергии, т.е. для нахождения Hт (без потерь), не обязательно знать состояние потока внутри колеса. Достаточно знать кинематические параметры течения до и после него. Связь между скоростями потока и энергией, сообщаемой жидкости, устанавливается с помощью теоремы количества движения.
Пусть элементарная струйка ограничена радиусами r1 и r2 и линиями тока и dQm – массовый расход через струйку
Тогда теорема количества движения запишется следующим образом
где dF – это сила, действующая на эту струйку
Применим теорему момента количества движения.
Согласно этой теореме момент количества движения элементарной секундной массы при переходе от одного сечения к другому равен моменту внешних сил, действующих между рассматриваемыми сечениями:
где dM - момент внешних сил
Скорости C1 и C2 c можно разложить на C1r , C1u и С2r, C2u . Причём радиальные проекции скоростей, т.е. C1r и C2r момента не дают (момент рассматривается относительно оси вращения наноса). Тогда:
Умножим обе части этого уравнения на ω (угловую скорость):
Получим уравнение Эйлера:
где dN=ωdM энергия, сообщаемая элементарной струйке в единицу времени

Суммарная мощность (теоретическая, без учёта потерь) |
или |
где C1u и С2u- осредненные по расходу окружные проекции скоростей.
Мощность Nт называется теоретической, т.е. не учитывающей механических и дисковых потерь. Nт – энергия, передаваемая мощности в единицу времени. Расход Qмт (массовый расход) является фактическим расходом жидкости через рабочее колесо, превышающим подачу мощности на величину утечек.
Теоретическая работа, подводимая к насосу для перемещения единицы массы жидкости
Давление |
|
|
|
Действительные значения Lт и Pт меньше на величину гидравлических потерь: |
|
|
|
Из треугольников видно: |
или |
тогда |
|
|
|
Кинетическая |
Потенциальная энергия |
|
|
энергия |
Теоретический статический напор |
Потенциальная энергия увеличивается как в относительном движении – за счёт уменьшения кинетической |
|||
энергии |
, так и в переносном движении |
|
|
если заменить абсолютную скорость – относительной в соответствии с зависимостью:
Очевидно, что возникновение потерь (напора, давления) в колесе связано в основном с циркуляционными силами. Значит, чем они меньше, тем меньше потери.
Из этого следует, что с возрастанием отношения m= r2/r1 кориолические силы растут, а циркуляционные силы падают и даже могут стать равными 0 и приобрести отрицательные значения, что положительно повлияет на значение гидравлического КПД.
Для колес с m 2 кориолические силы равны циркуляционным, что требует более тщательного профилирования рабочих решеток.
Энергия, |
Энергия, |
переданная циркуляционными силами |
переданная кориолическими силами |

Закон сохранения массы.
Закон сохранения массы, называемый также уравнением неразрывности, устанавливает равенство массовых расходов в двух или нескольких контрольных сечениях.
Закон сохранения энергии.
Для несжимаемой жидкости закон сохранения энергии носит название «Уравнение Бернулли».
Если в контрольных сечениях 1-1 и 2-2 поля скоростей равномерны, а геометрические отметки этих сечений относительно произвольной горизонтальной плоскости равны соответственно Z1 и Z2, то согласно уравнению Бернулли полные запасы энергии жидкости в этих сечениях отличаются на величину подведенной (или отведенной) энергии, включая гидравлические потери в трубопроводе между этими сечениями.
H - энергия, сообщённая 1 кг (вес) жидкости между сечениями 1-1 , 2-2
∆H - гидравлические потери
Из-за большой поверхности резервуаров (верхнего и нижнего) скорости C1 и C2 малы и их можно принять равными нулю. Тогда напор, развиваемый насосом равен
- статический напор, т.е.
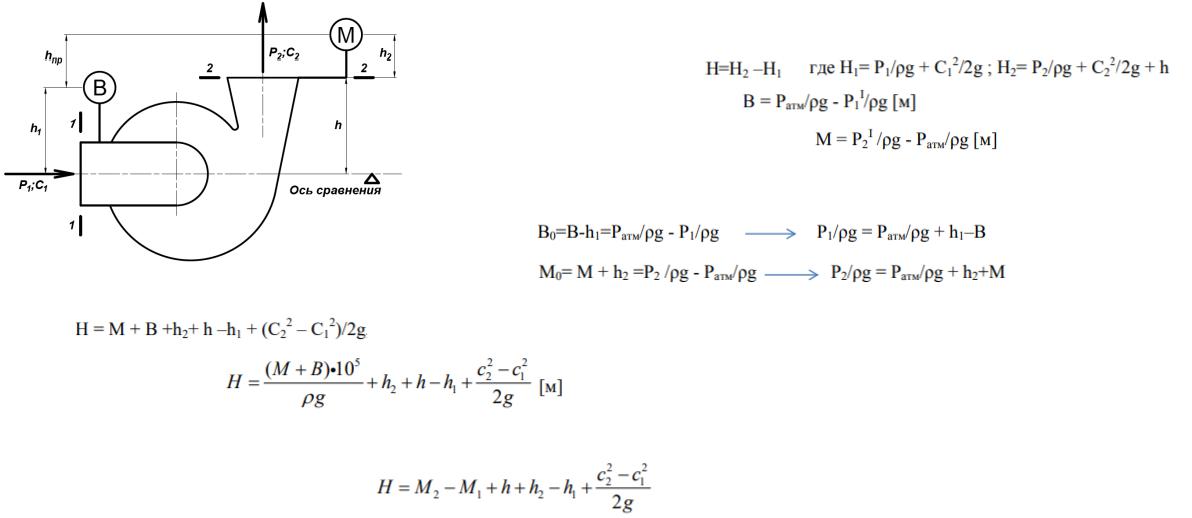
Определение напора насоса по показаниям приборов.
Если на входе в насос вакуум, а на выходе из насоса давление превышает атмосферное, то на входе в насос ставят вакуумметр (В) и на выходе манометр (М).
Напор Н, создаваемый насосом: |
|
Вакуумметр показывает разряжение: |
здесь Р1, Р2 - |
Манометр показывает избыточное давление: |
абсолютные |
давления. |
Приведем показания В и М к центрам тяжести плоскостей на входе в насос и на выходе (сечения 1-1 и 2-2 на рисунке), тогда:
тогда |
здесь М и В в [м]. |
если М и В в [кг/см2 ],то
Если на входе в насос избыточное давление (в этом случае на входе установлен манометр М1), то
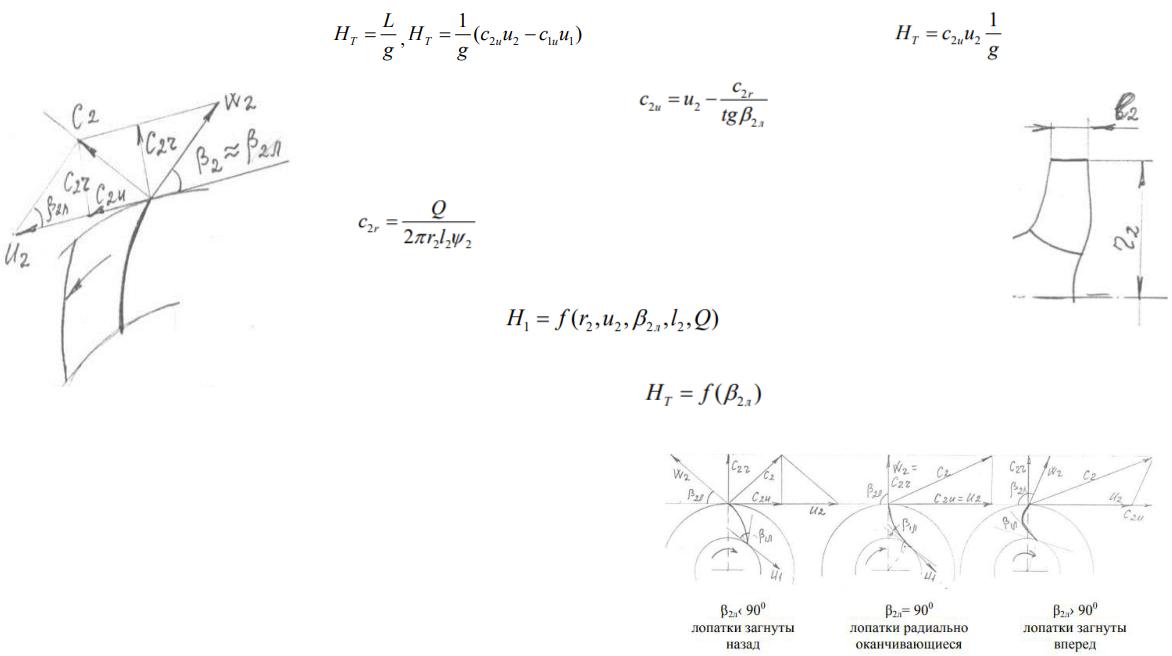
Теоретические характеристики насоса
Ранее было найдено выражение для |
т.к. С1u мало, то можно считать, что |
Далее из треугольника скоростей:
β2л > β2, но разница между ними небольшая, (β2л - β2) - угол отставания потока.
В знаменателе кольцевая площадь, через которую поток выходит из рабочего колеса, а ψ2 – коэффициент стеснения проходного сечения лопатками рабочего колеса на выходе, обусловлен тем, что лопатки имеют конечную толщину.
Таким образом:
Относительная скорость w в любой точке потока направлена по лопатке, найдем теоретический напор Hт, как функцию от угла β2л:
Рассмотрим насос, у которого r2 = const, l2= const, W=const, Q=const, при построении -ов надо иметь в виду, что U2=r2 W=const, С2r= const
Отсчёт угла β2л производится как от положительного, так и от отрицательного направления определения скорости. Принципиально способ отсчёта никакого значения не имеет. Обычно отсчёт производят от отрицательного направления окружной скорости.
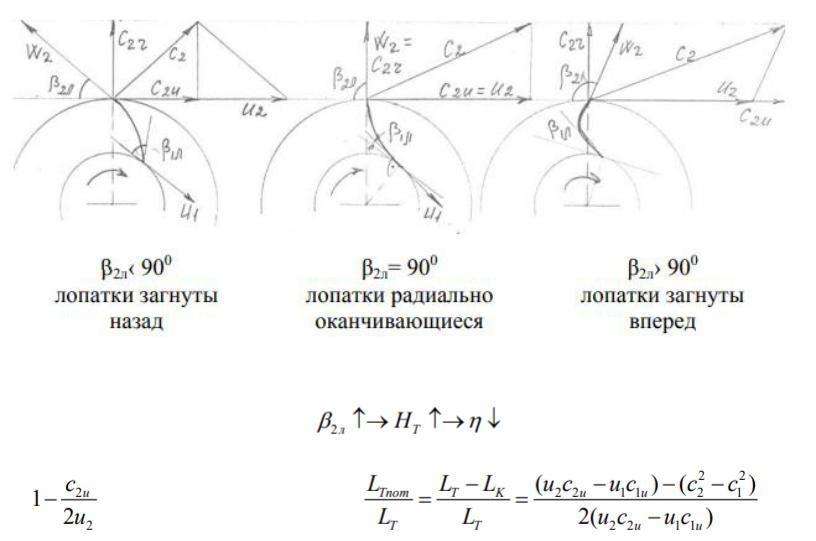
Из сравнения -ов видно, что при увеличении угла β2л увеличивается скорость С2u, следовательно, растет напор Hт, создаваемый насосом. Вместе с тем, при этом, увеличение скорости С2 приводит к увеличению потерь на трение при выходе потока жидкости из рабочего колеса и снижению КПД насоса.
Степень реакции = |
или степень реакции = |
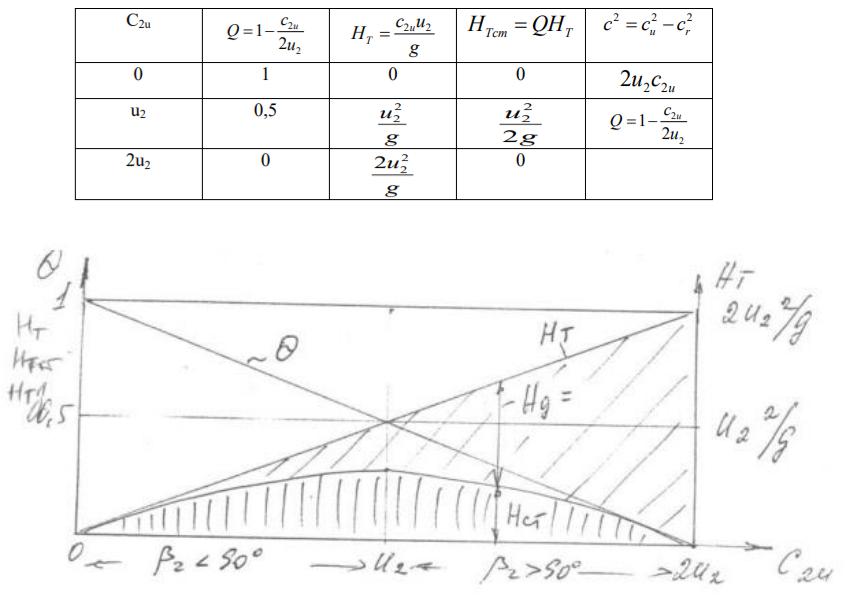
Зависимость теоретического напора и степени реакции от скорости С2u
|
|
|
При β2л 90 доля потенциальной энергии |
|
|
Нтст=Нт |
превышает долю кинетической. |
|
|
|
При β2л > 90 , наоборот, доля кинетической |
|
|
|
|
|
|
|
|
|
|
|
энергии превышает долю потенциальной. |
|
|
|
Насосы с лопатками загнутыми вперед позволяют |
|
|
|
получить при тех же габаритах больший напор, |
|
|
|
но при меньшем КПД. |
|
|
|
Радиально оканчивающиеся лопатки применяют |
|
|
|
в высокооборотных машинах, для того чтобы |
|
|
|
избежать возникновения значительных изгибных |
|
|
|
напряжений. |
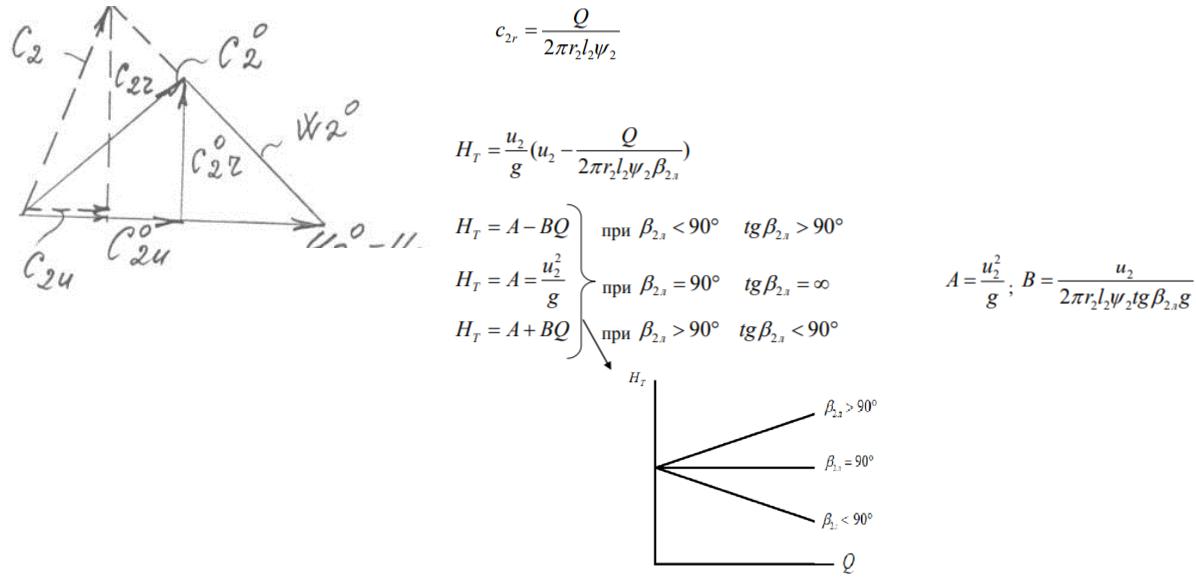
Зависимость теоретического напора от подачи и угла β2л
Построим два треугольника скоростей. Один при исходной подаче (скорости индексом «0 »), а другой при повышенной.
т.к.
то при росте подачи Q скорость C2r тоже будет расти.
Из треугольника видно, что в это же время скорость С2u падает.
Запишем уравнение для теоретического напора
здесь
Уравнения прямых линий
