Добавил:

Chupapi_Munyanya Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МЭИ»

Предмет:

Турбомашины АЭС

Файл:

Насосы / ПОСОБИЕ Насосы АЭС

.pdf

Скачиваний:

Добавлен:

16.05.2024

Размер:

2.93 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 97 8 9 > Следующая >>>

Тогда проекция скорости c2 на окружное направление:

c	u	2	L	12000 109,54 м.
2u		2	T	с
				с

Из треугольников скоростей:

c		c2	c2	109,542 202	111,35 м.
	2	2u	2r		с
					с

Значение степени реактивности θ для этого варианта колеса:

θ 1	c2	c	2	1	111,352 202	0,5.
θ 1	2	1		1	2 12000	0,5.
	2 L				2 12000
		T

3.4. Определение напора насоса по показаниям приборов

Задача № 3.4.1

При испытании насоса получили следующие данные: объемную подачу Q = 6,5 л/с, показания вакуумметра Ввх = 294 мм.рт.ст., показания манометра Мвых = 0,35 МПа, крутящий момент на валу Мкр = 41 Н м при скорости вращения колеса насоса n = 800 об/мин. Скорости с1 и с2 равны. Найти мощность, потребляемую насосом Nпотр, полезную мощность Nпол и КПД насоса ηн.

Пояснения к решению задачи:

На входе в насос находится вакуумметр, а на выходе – манометр (см. рис. 3.4.1). Скорость воды на входе в насос c1, а на выходе – c2.

Рис. 3.4.1

Решение

Напор Н определяется из уравнения Бернулли:

	p	c2		p	c2	H H.
1	1	1	2	2	2
	ρg	2g		ρg	2g

Поскольку c1 = c2, Z1 = Z2 = 0 и ∆Н = 0, то напор, развиваемый насосом равен:

H ρpg2 ρpg1 1g (M Bвх ).

H 1014 (0,35 106 0,294 10 13,6 103) 39 м.

При этом учтено, что вакуумметр показывает разряжение, а манометр избыточное давление.

Т.е.

p2 Mвых Pатм ; p1 Pатм Ввх.

Полезная мощность насоса:

Nпол ρgQH 104 6,5 10 3 39 2535 Вт.

Мощность, потребляемая насосом:

Nпотр Mкрω Mкр 2π n 41 80060 2π 3435 Вт.

Здесь ω – скорость вращения колеса насоса в радианах. КПД насоса определяется зависимостью:

ηН Nпол 2535 0,738.

Nпотр 3435

Задача № 3.4.2

Центробежный насос, приведенный на рисунке 3.4.2, прошел испытания при объемной подаче Q = 250 л/с. При этом по показаниям вакуумметра Рвх = 0,4 кг/см2, по показаниям манометра Рвых = 3,3 кг/см2.

Диаметры всасывающего и напорного патрубков одинаковы. Высота hпр = 0,8 м. Мощность, забираемая электродвигателем из сети Nэ = 128 кВт. КПД электродвигателя ηэ = 0,95. Найти полезную мощность Nпол, КПД насоса ηн и насосного агрегата ηна.

Решение

Величина напора Н определяется из уравнения Бернулли:

H М h2 h B h1 c222gc12 М B Ζ c222gc12 .

Обозначим (h2 h) h1 , т.е. Z=hпр; М Pρвыхg ;В ρPвхg . Тогда выражение для напора:

H ρ1g (Pвых Pвх ) 33 4 0,8 37,8 м.

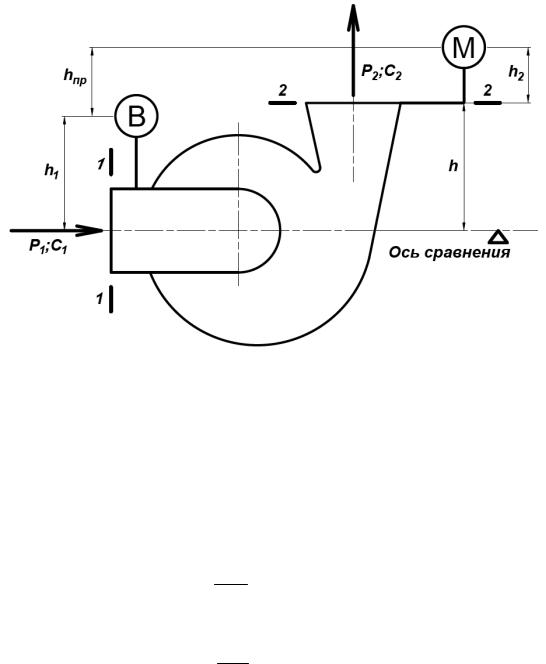
Рис. 3.4.2

Полезная мощность насоса:

Nпол ρgQH 1000 9,8 250 10 3 37,8 92610 Вт 92,61кВт.

Мощность на валу:

NВ Nэηэ 128 103 0,95 121600 Вт 121,6 кВт.

КПД насоса:

ηН Nпол 92,61 0,762.

Nв 121,6

КПД насосного агрегата:

ηна Nпол 92,61 0,724.

Nэ 128

Задача № 3.4.3

При испытании центробежного насоса (см. рис. 3.4.2.) за 720 секунд расход жидкости составил G = 87,6 м3. При этом по показаниям вакуумметра Рвх = 0,42 кг/см2, по показаниям манометра Рвых = 10,2 кг/см2. Диаметр всасывающего патрубка dвс = 300 мм, а напорного патрубка dнап = 250 мм. Высота hпр = 0,64 м. Расход электроэнергии за 12 мин 10 с составил 31,4 кВт ч.

Определить полезную мощность насоса Nпол, мощность, забираемую из сети Nэ и КПД насосного агрегата ηна.

Решение

Из уравнения Бернулли напор по показаниям манометра и вакуумметра:

H М h2 h B h1 c222gc12 М B c222gc12 . Здесь М и В в [м].

М Pρвыхg ; В ρPвхg ; Z = hпр.

Объемная подача:

Q	G	87,6	0,122	м3	.
	720	720		с

Скорости c1 и c2 определяются по уравнению неразрывности.

		c		Q 4					0,122 4			1,727	м	;
		c		πd 2				3,14 0,32				1,727	с	;
		1		πd 2				3,14 0,32					с
					1
		c	Q 4						0,122 4			2,487 м.
		c		πd22			3,14 0,252					2,487 м.
		2		πd22			3,14 0,252						с
Тогда напор, создаваемый насосом:
			1									c2 c2
		H			(P P ) 2								1
		H		ρg	(P P ) 2								1
				ρg		вых				вх		2g
	1	10,2 0,42							5		2,4872 1,7272
						10				0,64		2 10		107,0 м.
	1000 10					10				0,64		2 10		107,0 м.

Полезная мощность насоса:

Nпол gρQH 10 1000 0,122 107,0 13054 Вт 130,54 кВт.

Мощность, забираемая из сети:

Nэ Э 31,4 3600 157,0 кВт. Т 720

КПД насосного агрегата:

ηна Nпол 130,54 0,831.

Nэ 157,0

3.5. Применение теории подобия в расчетах при проектировании насосов. Пересчет характеристик насосов

Задача № 3.5.1

При работе насоса были повреждены выходные кромки лопаток в результате задевания рабочего колеса. Для исправления колесо было проточено и его диаметр уменьшился на 3%, а выходной угол увеличился на 1˚.

Для исходного колеса насоса (c2r/u2)м = 0,195, β2м = 18°.

Скорость вращения колеса насоса после ремонта не изменилась. Определить во сколько раз изменится напор и подача насоса.

Рис. 3.5.1

Решение

Таким образом, после ремонта отношение наружного диаметра колеса после ремонта и исходного колеса:

d2 0,97. d2м

Угол выхода потока из отремонтированного колеса: β2 β2м 1 18 1 19.

Скорость вращения колеса осталась неизменной. Поэтому для пересчета подачи используем следующую зависимость в соответствии с теорией подобия, учитывая влияния изменения угла β2:

			d2	3
Q	λ3				0,973 0,913.
Qм
		d2м

Оценим влияние изменения β2. Отношение расходных составляющих абсолютных скоростей потока на выходе из колес:

w sinβ

sinβ

0,97 sin190

1,02.

sinβ

2м

sin18

2rм

2м

С учетом того, что:

, u πdn .

w2м

u2м

Тогда отношение подач для отремонтированного и исходного колеса составит:

Q Q 1,02 0,913 1,02 0,931.

Qм Qм

Отношение напоров для отремонтированного и исходного колеса составит:

u22(1

c2r

ctgβ2)

u22(1 c2rм

sinβ2 ctgβ2)

2м

sinβ

2м

Hм

c2rм

u2м(1

u2м

ctgβ2м)

u2м(1

u2м

ctgβ2м)

0,195

cosβ

cos190

1 0,195

sinβ2м

0,97

sin18

0,949,

(1 0,195 ctgβ2м)

0,195 ctg180

d2м

где

c2r c2rм

sinβ2 .

u2м

sinβ2м

Задача № 3.5.2

Рассчитать геометрические характеристики насоса (диаметр колеса на выходе d2 и длину лопатки l2), используя метод моделирования. Для реального насоса подача должна быть равна Q = 2,7 м3/мин, напор H не менее 20 м, скорость вращения колеса насоса n = 50 с–1. Для модельного насоса подача равна Qм = 6,7 м3/мин, скорость вращения колеса насоса nм = 50 с–1.

Размеры модельного насоса: d2м = 0,220 м, l2м = 0,02м, β2м = 200, ψ2 = 0,96.

Решение

Из уравнения Эйлера определим значение напора для модельного насоса:

2rм

34,562

8,42

Hм

2м 1

ctgβ2м

9,8

34,56

ctg20

40,295м,

u2м

Где окружная скорость на внешнем диаметре модельного колеса: u2м πd2мn π 0,22 50 34,56 мс ,

а расходная составляющая скорости потока на выходе из модельного колеса насоса из уравнения неразрывности:

c		Qм				6,7	8,42	м.
	πd	l	ψ		π 0,22	0,02 60 0,96
2rм				2				с
		2м 2м

Здесь ψ – коэффициент стеснения, учитывающий уменьшение реальной площадивыходапотокаизколесаиз-заопределеннойтолщинылопаток.

Найдем коэффициент пропорциональности λ и найдем наружный диаметр колеса из соотношения подач.

Q	λ3	n	,
Q	λ3	n	,
Q		n
м		м

где λ = d2/d2м. Поскольку n = n2м

d2 d2м 3	Q	0,22 3	2,7	0,162 м.
d2 d2м 3	Q	0,22 3	6,7	0,162 м.
	м

При этом значении d2

определим напор по зависимости теории по-

добия:

2м

0,162 2

H Hмλ

Hм

40,295

21,85 м.

d2м

0,220

Условие задачи выполняется. Определим длину лопатки. Поскольку l2/d2 = l2м/d2м, то

l2 d2 l2м 0,162 0,02 0,0147 м. d2м 0,22

Задача № 3.5.3

Определить наружный диаметр колеса насоса d2, если его подача Q = 23,18 м3/с, напор H = 100 м, скорость вращения колеса насоса n = 450 об/мин.

Решение

Для данного насоса рассчитывается коэффициент быстроходности:

n 3,65 n		Q 3,65 450	23,18 250.
s	H 3 4	1003 4

В справочнике находим параметры насоса, имеющего такой же коэффициент быстроходности: Q0 = 1,5 м3/с, H0 = 50м, n0 = 400 об/мин, d20 = 0,5 м.

Тогда коэффициент пропорциональности:

n0	H	400	100	1,257.
		450	50
n	H0

Наружный диаметр насоса:

d2 d20 λ 0,5 1,257 0,6285 м.

	Задача № 3.5.4
	Известны действительные характеристика вентилятора Р = f	(Q) и
N =	f (Q) (см. табл. 3.5.1 и рис. 3.5.2). Плотность газа ρ	= 1,2
кг/м3	, скорость вращения колеса n = 150 с–1, наружный диаметр

колеса d2 = 0,4 м. Построить характеристики η= f (Q), РI= f (Q´), NI= f (Q´) и

ηI=	f (Q´) геометрически подобного вентилятора при ρ´ = 0,98
кг/м3	,d´2 =0,5м,n´ =100с–1.

Решение

Проводится пересчет параметров работы вентилятора по зависимостям теории подобия с учетом изменения плотности газа, скорости вращения колеса и наружного диаметра колеса. Зависимость, связывающая значение подачи нового вентилятора и исходного:

		Qλ	3 n					d2		3	n					0,5 3								100
	Q	Qλ			n	Q					n		Q											150	1,302 Q.
					n			d2			n					0,4								150
	Зависимость, связывающая значение давления нового вентилятора
и исходного:
				2			2				0,5			2			100				2			0,98
	p pλ			2	n			ρ			0,5						100							0,98		0,567p.
	p pλ					n		ρ		p							150							1,2		0,567p.
						n		ρ			0,4						150							1,2
	Зависимость, связывающая значение мощности нового вентилятора
и исходного:
				5			3				0,5			5			100			3			0,98
	N	Nλ		5	n			ρ			0,5						100						0,98			0,738 N.
	N	Nλ				n		ρ		N							150							1,2		0,738 N.
						n		ρ			0,4						150							1,2
	КПД исходного вентилятора определится по зависимости:
									η		Nпол					pQ		.
									η									.
												N					N
	КПД нового геометрически подобного вентилятора определится по
зависимости:

											Nпол				p Q
									η										.
									η		N						N		.
	Результаты расчета приведены в табл.3.5.1 и на рис.3.5.2.
																						4800					Таблица 3.5.1
	Q, м3/час	0						2000					4000									4800					6000	8000
	P, Па	540						435					465										480				475	410
	N, кВт	0,4						0,60					0,92										1,1				1,42	1,98
	η	0						0,403					0,562									0,582					0,558	0,460
	Q´, м3/час	0						2604					5208								6249,6						7812	10416
	P´, Па	306,2						246,6					263,7									272,2					269,3	232,5
	N´, кВт	0,295						0,443					0,679									0,812					1,048	1,461
	η´	0						0,403					0,562									0,582					0,558	0,460

Рис. 3.5.2

Задача № 3.5.5

Известна характеристика насоса Н = f (Q) и КПД насоса ηн = f (Q) при скорости вращения колеса n = 1 500 об/мин (см. рис. 3.5.3). Плотность перекачиваемой жидкости ρ = 1 000 кг/м3.

1.Построить характеристики данного насоса при новой скорости вращения колеса, равной 3 000 об/мин и 1 000 об/мин.

2.Построить зависимость потребляемой мощности насоса Nпотр в зависимости от подачи при n = 1 500 об/мин и n = 3 000 об/мин.

Рис. 3.5.3

Решение

Обозначим характеристики насоса для скорости вращения колеса насоса 1 500 об/мин: Q, Н, n, Nпотр; для скорости вращения колеса насоса 1 000 об/мин: Q', Н', n', N'потр; для скорости вращения колеса насоса

3000 об/мин: Q'', Н'', n'', N''потр.

Пересчет напора и подачи проводится по зависимостям теории подобия. КПД насоса ηн при пересчете параметров остается неизменным.

ηн ηн ηн.

;Q Q

H H

;H H

; Q Q

Nпол

ρgHQ

Nпол

ρgH Q

Nпотр

;

Nпотр

ηН

Nпотр Nпол ρgH Q . ηН ηН

Результаты расчетов приведены в табл. 3.5.2 и на рис. 3.5.4.

					Таблица 3.5.2

Q, м3/с	0	0,1	0,2	0,3		0,4
H, м	30	27,5	25	20		10

ηн= η'н= =η''н	0	0,6	0,9	0,75		0,45

Nпотр, кВт	0	44,917	54,444	78,400		87,111

Q', м3/с	0	0,0667	0,1334	0,2001		0,2668
H', м	13,350	12,238	11,125	8,900		4,450
N'потр кВт	0	13,332	16,160	23,270		25,856

Q'', м3/с	0	0,2	0,4	0,6		0,8
H'', м	120	110	100	80		40

N''потр кВт	0	359,333	435,556	627,200		696,889

Примечание: в действительности при Q = 0 потребляемая мощность не равна 0, а равна мощности холостого хода. Поэтому расчет потребляемой мощности в зависимости от подачи следует проводить для значений Q > 0.

Зависимости Nпотр= f(Q), Н' = f(Q'), N'потр= f(Q'), η'н= f(Q'), Н'' = f(Q''), N''потр= f(Q'), η''н= f(Q'') представлены на рис. 3.5.4.

<<< < Предыдущая 1 2 3 4 5 67 / 97 8 9 > Следующая >>>

Соседние файлы в папке Насосы

#
16.05.20241.12 Mб15Вопросы из билетов к зачету по курсу_Турбомашины АЭС (2).pdf
#
16.05.2024227.28 Кб11Дата и место проведения зачета.pdf
#
16.05.20242.93 Mб78ПОСОБИЕ Насосы АЭС.pdf