Турбины / Лекции / Лекци 8

Лекция №8 Расчет ступени, работающей на влажном паре : расчет длины сопловых и рабочих лопаток; абсолютных и относительных скоростей с учетом поправок на влажность; построение треугольников скоростей для перегретого пара и влажного; выбор профилей сопловых и рабочих решеток;

Расчет ступени, работающей на влажном паре, включает в себя расчет геометрических характеристик сопловых и рабочих лопаток, построение треугольников скоростей, построение процесса в h-s диаграмме, определение потерь энергии в ступени и коэффициентов полезного действия. Расчеты проводятся с учетом поправок на влажность.

Кроме того, определяется мощность ступени, определяются параметры пара перед следующей ступенью, проводится расчет на прочность рабочей лопатки. Если после данной ступени организована периферийная сепарация, то расход пара в следующую ступень рассчитывается с учетом отбора влаги и пара при сепарации.

Методика расчета ступени, работающей на влажном паре

Исходные данные для расчета:

расход пара G

параметры пара на входе в сопловую решетку: давление Р0 и

степень сухости Х0

степень крупнодисперсности λ

скорость пара на входе в сопловую решетку С0

средний диаметр ступени dср

угол выхода потока пара из сопловой решетки α1Э

скорость вращения ротора n

степень реактивности ступени на среднем диаметре ρср

1.Расчет ступени паровой турбины начинается с расчета (u/Cф)опт для того,

чтобы кпд ступени был наибольшим.

(u/Cф)опт= 1 2√(1−ср)

2.Выбирается (u/Cф) немного меньше , чем (u/Cф)опт, чтобы получить наибольшее значение относительного лопаточного кпд

распологаемый термоперепад ступени по параметрам торможения Н0,= Cф2/2

распологаемый термоперепад сопловой решетки по параметрам

торможения Н0с= (1- ср) Н0,

распологаемый термоперепад рабочей решетки Н0р= ср Н0

5. Начнем строить процесс расширения пара в ступени в h-s диаграмме:

От т. 0 отложим вверх отрезок, равный с20 /2 и получим параметры

торможения пара Р0 и t0

От т. 0 отложим вниз Н0с=Н0с - с20 /2 и получим точку 1t. В этой точке найдем величины давления Р1, удельного объема V1t и степень сухости

Х1t

6.Определим абсолютную теоретическую скорость на выходе из сопловой решетки

7.Длина сопловой лопатки в предположении, что коэффициент расхода в

сопловой решетке µ1=1:

8. Определим µ1 с учетом поправки на влажность пара: µ1= µ1ʺ + ∆µ1ʹ

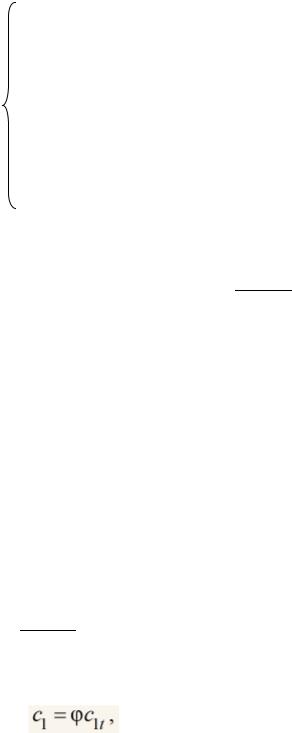
зададим хорду сопловой решетки b1 и определим b1/l1

число Рейнольдца Re1t=b1C1t/υ1

здесь υ1 – кинематическая вязкость пара на выходе из сопловой решетки

∆α= 180-(90+ α1)

Sinα0/Sin α1Э

Эти данные позволяют определить для перегретого пара µ1ʺ, а также относительные потери энергии для перегретого пара в сопловой решетке ζсʺ и определить коэффициент скорости для перегретого пара

в сопловой решетке φʺ= √1 − ζʺс

Для определения поправки на влажность ∆µ1ʹ используются следующие величины: у0, λ, ε1 =Р1/Р0

∆µ1ʹ = ∆µ0ʹ·Кε

9. Для определения поправки на влажность ∆ζсʹ используются следующие величины: у0, λ

Тогда относительные потери энергии для влажного пара в сопловой решетке ζс = ζсʺ + ∆ζсʹ

10.Коэффициент скорости для влажного пара в сопловой решетке

φ = √1 − ζс

11.Определим действительную абсолютную скорость на выходе из сопловой решетки (в т. 1)

12.Определение угла выхода потока пара из сопловой решетки при течении влажного пара

α1 = α1Э + ∆α1 ∆α1 = у0·∆α1ʹ + (1- у0) ∆α1ʺ

∆α1ʹ - поправка для влажного пара и ∆α1ʺ- поправка для перегретого пара определяются по величинам у0 и λ

13. Уточним значение длины сопловой лопатки l1 по значению коэффициента расхода µ1

14.Построим входной треугольник скоростей по найденным значениям С1, α1, u. Из входного треугольника скоростей определим угол β1 и относительную скорость выхода из сопловой решетки W1

15.Абсолютные потери в сопловой решетке :

С2 С2

∆Нс= 21t − 21

16.Выберем профиль сопловой решетки по значениям: α0=900

α1

М1t=C1t/a1t , где a1t=√1 1

Например С-90-15А 17. Определим относительную теоретическую скорость пара на выходе из рабочей решетки

W2t = √12 + 20

18.Длина рабочей лопатки

l2 = l1 + ∆l

здесь ∆l – перекрыша

19. Задаем коэффициент расхода через рабочую решетку µ2=1 и определяем из уравнения неразрывности угол β2Э

20.Определим степень реактивности в корневом сечении ρк при заданном законе закрутки. Полученное значение ρк должно находиться в диапазоне от

0,05 до 0,1

21.Определим µ2 с учетом поправки на влажность пара:

µ2= µ2ʺ + ∆µ2ʹ

зададим хорду рабочей решетки b2 и определим b2/l2

число Рейнольдца Re2t=b2 W2t /υ2

здесь υ2 – кинематическая вязкость пара на выходе из рабочей решетки

∆β2= 180-( β 1 + β 2) Sin β 1/Sin β 2

Эти данные позволяют определить для перегретого пара µ2ʺ

, а также относительные потери энергии для перегретого пара в рабочей решетке ζрʺ и определить коэффициент скорости для

перегретого пара в сопловой решетке ψʺ= √1 − ζʺр

Для определения поправки на влажность ∆µ2ʹ используются следующие величины: у1, λ1, ε1 =Р2/Р1

Степень влажности на входе в рабочую решетку у1 определяем по h-s

диаграмме: т.1 найдем, если отложим потери в сопловой решетке ∆Нс от т.1t

λ1= λ0 у1

у0

∆µ2ʹ = ∆µ0ʹ·Кε

22. Для определения поправки на влажность ∆ζрʹ используются следующие величины: у1, λ1

Тогда относительные потери энергии для влажного пара в рабочей решетке ζр = ζрʺ + ∆ζрʹ

23.Коэффициент скорости для влажного пара в рабочей решетке

ψ = √1 − ζр

24.Определим действительную относительную скорость на выходе из рабочей решетки (в т. 2)

W2 = ψ W2t

25.Определение угла выхода потока пара из рабочей решетки при течении

влажного пара

β2 = β2Э + ∆ β2

∆β2 = у1·∆ β2ʹ + (1- у1) ∆ β2ʺ

∆β2ʹ - поправка для влажного пара и ∆ β2ʺ- поправка для перегретого пара

определяются по величинам у1 и λ1

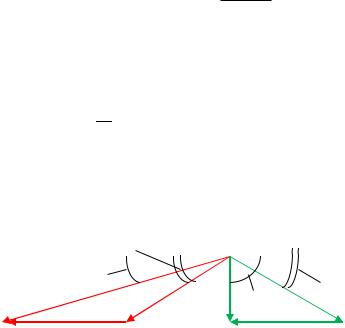
26.Построим выходной треугольник скоростей по найденным значениям W2, β2, u. Из выходного треугольника скоростей определим угол α2 и абсолютную скорость выхода из рабочей решетки С2

27.Абсолютные потери в рабочей решетке :

W2 W2

∆Нр= 22t − 22

28.Выберем профиль рабочей решетки по значениям:

β1 β2

М2t=W2t/a2t , где a2t=√2 2

Например Р-35-25А

29.Определим потери с выходной скоростью

С2

∆Нвс = 22

30.Процесс в h-s диаграмме

31. Треугольники скоростей