НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ

«МЭИ»

кафедра АЭС

Лабораторная работа № 6

Определение длины диффузии для графита методом сигма-призмы

Группа: ТФ-12-20

Бригада:

Студент: Долгов Р.Н.

Преподаватель: Лунчев Ю.В.

Шпаковский А.А.

Дата выполнения работы: 02.04.24

Москва 2024

Цель работы. Введение

Для решения многих задач теории реакторов необходимо знание одного из важнейших параметров процесса диффузии нейтронов — длины диффузии. Все методы непосредственного экспериментального определения длины диффузии L основаны на измерении пространственного распределения тепловых нейтронов в среде без источников. Особенно просто задача решается для среды таких размеров, при которых практически все нейтроны источника поглощаются в среде. Для создания такой «бесконечной» среды необходимо, чтобы эффективный диаметр ее области составлял приблизительно 30 длин диффузии. Ясно, что создать практически «бесконечную» среду замедлителя можно лишь для воды и некоторых водородосодержащих веществ. В случае таких замедлителей, как тяжелая вода и графит, эксперименты проводятся в средах, размеры области которых сравнимы с длиной диффузии, вследствие чего необходимо учитывать утечку нейтронов из среды.

Один из используемых методов измерения длины диффузии называется методом сигма-призмы. Сигма-призма представляет собой неразмножающую среду исследуемого вещества, обычно замедлителя, с прямоугольной или цилиндрической формой. Нейтроны либо вводятся через торец призмы, либо испускаются точечным источником, расположенным в самой призме вблизи ее основания.

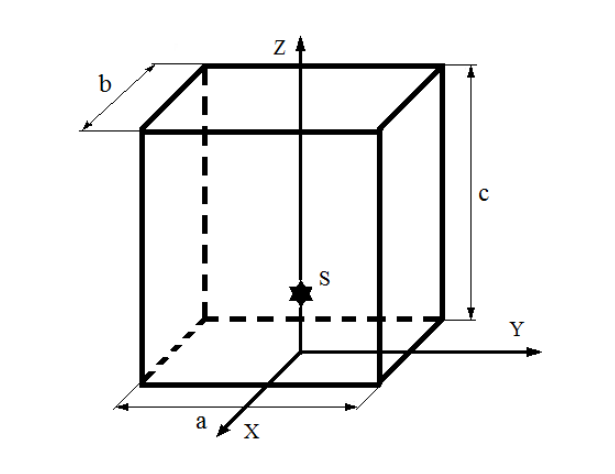
Рис. 1. Сигма-призма

Рассмотрим графитовую сигма-призму в виде прямоугольного параллелепипеда размерами a x b x c (рис. 1). Начало координат поместим в центре основания призмы. Пусть в точке с координатами (0, 0, z₀) расположен источник быстрых нейтронов. Для определения длины диффузии необходимо измерить пространственное распределение потока тепловых нейтронов; затем следует сравнить его с теоретическим, что позволит найти искомую величину. Однако аналитическое выражение для пространственной зависимости потока тепловых нейтронов, образующихся в результате замедления в исследуемой среде быстрых нейтронов источника, в общем виде настолько громоздко, что ручные расчеты становятся невозможными. Поэтому обрабатываются результаты лишь тех измерений, которые проводятся в области призмы, настолько удаленной от источника нейтронов, что в ней отсутствуют быстрые нейтроны, т.е. имеются только источники тепловых нейтронов. В этой области пространственное распределение потока тепловых нейтронов описывается достаточно простым аналитическим выражением. Исключить влияние быстрых нейтронов можно и другим способом — использованием метода кадмиевой разности. Для этой цели применяется съемная кадмиевая пластина, перекрывающая все поперечное сечение призмы. Тогда разность результатов двух измерений (без кадмиевой пластины и с установленной кадмиевой пластиной) будет пропорциональна потоку тепловых нейтронов от их источника, расположенного в плоскости кадмиевой пластины.

Получим выражение для пространственной зависимости потока тепловых нейтронов в области призмы, расположенной над источником нейтронов и удаленной от него настолько, что в ней имеются лишь тепловые нейтроны. В стационарных условиях уравнение диффузии будет иметь вид

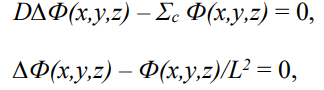
где Ф(х,y,z) — пространственное распределение потока тепловых нейтронов; D — коэффициент диффузии; Σ_с — макроскопическое сечение радиаионного захвата для графита в области тепловых нейтронов; L — длина диффузии для графита.

Уравнение необходимо дополнить граничными условиями:

где a_э, b_э, с_э — экстраполированные размеры призмы.

Решение уравнения ищем в виде

Ф(х,y,z) = Ф(х) Ф(y) Ф(z)

Подставляя решение в исходное уравнение и разделив полученное выражение на Ф(х,у,z), имеем

Так как граничное условие предполагает допустимость разделения переменных, то можно записать

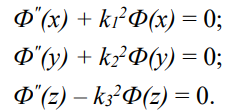
Общие решения уравнений соответственно имеют вид:

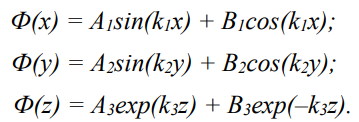
Из условия симметрии следует, что A₁ = А₂ = 0. Из граничных условий также следует, что А₃ = — B₃ exp(–2k₃c_э) и

k_1n = π / a_э (2n + 1), n = 0, 1, 2, … ;

k_1m = π / b_э (2m + 1), m = 0, 1, 2, …

Отметим, что определить знаки перед k₁² , k₂² и k₃² можно, строго говоря, лишь используя граничные условия. Действительно, допустим, что равенство мы запишем в виде

k₁²+ k₂²+k₃² = 1/L²

тогда общее решение для Ф(х) будет иметь вид

Ф(x) = A₁exp(k₁x) + B₁exp(–k₁x).

Это решение при любых действительных k₁ ≠ 0 не удовлетворяет первому из граничных условий. Абсолютно аналогичное положение было бы и с Ф(y). Но в то же время величина 1/L² заведомо больше нуля, откуда следует, что перед k₃² должен стоять знак «плюс» и k₃² должно быть больше (k₁² + k₂²). Во всех этих рассуждениях мы предполагаем, что все k_i — действительные константы.

Таким образом, окончательное выражение для Ф(х,у,z) будет иметь вид бесконечного ряда:

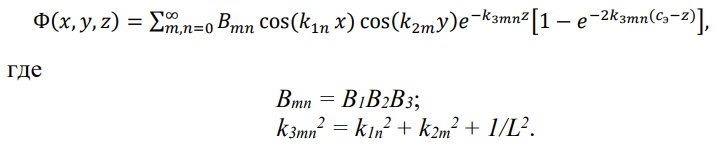
видно, что вклад высших гармоник в ряд резко уменьшается с увеличением z. Поэтому достаточно далеко от источника ряд превращается в выражение

Сравним уравнение для Ф(z) и решение с уравнением и решением для случая плоского источника тепловых нейтронов, расположенного в плоском слое экстраполированной толщиной 2с_э. Заметно формальное совпадение этих уравнений и их решений, если считать, что в нашем случае в плоскости (х, у, 0) расположен плоский источник тепловых нейтронов мощностью пропорциональной cos(k₁₀x)∙cos(k₂₀y), а исследуемая среда имеет длину диффузии (релаксации), равную 1/k₃₀₀. Такое совпадение имеет достаточное физическое объяснение. Действительно, пространственное распределение потока тепловых нейтронов в исследуемой призме обусловлено, с одной стороны, геометрическими характеристиками и спектром нейтронов источника, а с другой — геометрическими характеристиками призмы и процессами замедления нейтронов источника и диффузии тепловых нейтронов по всему поперечному сечению призмы. Ясно, что на достаточно большом расстоянии от источника определяющими факторами будут геометрические характеристики призмы и процесс диффузии тепловых нейтронов, в результате чего и будет справедливо выражение. В то же время вблизи источника важными будут все факторы, вследствие чего в этой области призмы Ф(х, у, z) имеет вид бесконечного ряда, в общем случае значительно более сложного, чем начальный ряд.

В случае, когда точечный источник испускает тепловые нейтроны, процесс замедления последних, конечно же, не имеет места, однако вблизи такого источника процесс диффузии нейтронов по-прежнему определяется геометрическими характеристиками источника и призмы, что приводит к справедливости в этой области распределения.

Таким образом, с интересующей нас точки зрения качественно два этих случая одинаковы, а различие заключается лишь в том, что распределение устанавливается, начиная с разных значений z. Последние зависят от соотношения между длиной диффузии L и длиной замедления √τ. Для графита и калифорниевого источника нейтронов L > √τ и плотность замедления снижается значительно быстрее с увеличением расстояния от источника, чем поток тепловых нейтронов. Поэтому приближенно можно считать, что если пространственная зависимость потока тепловых нейтронов, начиная с какого-то значения z, описывается выражением при использовании точечного источника тепловых нейтронов, то при использовании точечного источника быстрых нейтронов в той же области призмы с удовлетворительной точностью также справедливо выражение

Из выражения видно, что при с_э → ∞ получаем для Ф(z) следующее выражение:

Ф(z) = B₃ e ^−k300z.

Значит, множитель 1 − e^{−2k300(cэ−z)} учитывает влияние внешней границы призмы на пространственное распределение потока тепловых нейтронов. Если расстояние от верхней грани (с_э − z) составляет порядка нескольких длин релаксации тепловых нейтронов 1/k₃₀₀, то влиянием верхней границы можно пренебречь. Из приведенного выше следует, что зависимость потока тепловых нейтронов Ф_Т от координаты z для призмы имеет вид кривой, приведенной на рис. 2.

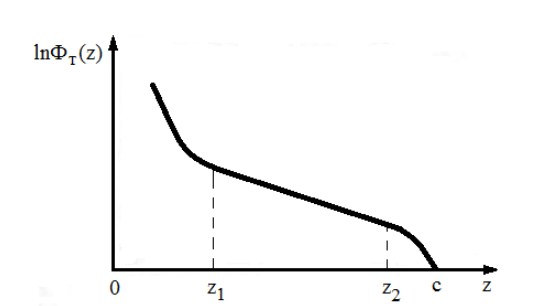
Рис. 2.

Вблизи источника справедливо распределение в виде бесконечного ряда, затем идет участок z₁—z₂ экспоненциального изменения Ф(z) и далее — участок с распределением. Для определения длины диффузии измеряют распределение потока тепловых нейтронов в относительных единицах по оси z и в результате обработки линейного участка зависимости lnФ_Т(z) = f(z) определяют значение k₃₀₀.

Для расчета длины диффузии L можно воспользоваться выражением, которое имеет вид

Экстраполированные размеры призмы а_э и b_э можно определить несколькими способами. Если провести измерения зависимостей Ф от координат х и у в области, где вклад высших гармоник пренебрежимо мал, то а_э и b_э можно определить либо графическим способом, либо (более точно) путем обработки экспериментальных данных методом наименьших квадратов. Поскольку экстраполированные размеры призмы обычно мало отличаются от геометрических, то их можно определить и прибавлением к геометрическим размерам значения 2ξ = 2∙0,71∙λ_tr (λ_tr - транспортная длина пробега для тепловых нейтронов, взятая из литературы), не получая при этом большой погрешности расчета L.

Оценим размеры призмы, необходимые для достаточно точного определения длины диффузии. Если пренебречь погрешностью в определении экстраполированных размеров а_э и b_э, то следует, что относительная погрешность ∆L/L связана с относительной погрешностью ∆k₃₀₀ / k₃₀₀ соотношением

Видно, что геометрические размеры призмы существенно влияют на погрешность расчета L. Например, если а_э = b_э = L, то 1 + L²π² ( 1 / a_э² + 1 b_э²) ≈ 20. Значит, погрешность расчета L в 20 раз больше погрешности определения k₃₀₀. Поэтому размеры поперечного сечения призмы должны равняться примерно (2-3) L. Высота призмы должна быть такой, чтобы существовала достаточно большая (удобная для проведения измерений) область экспоненциальной зависимости Ф(z). Это достигается, если высота призмы равна примерно (3-5) L.

Целью данной работы является экспериментальное определение длины диффузии для графита методом сигма-призмы.