Лабы / 5 (направильно посчитано) / ЛР5 Долгоа Р ТФ-12-20

Цель работы. Введение

Одной из наиболее важных характеристик отражателей ядерных реакторов является коэффициент диффузного отражения нейтронов - альбедо. Альбедо определяется как вероятность того, что нейтрон, падающий на поверхность (границу) какого-либо вещества, выйдет из него обратно. Отражение нейтронов веществом происходит вследствие того, что в процессе диффузии в веществе нейтрон после ряда рассеяний может выйти из него. Ясно, что направление вылета нейтрона из вещества не зависит (в первом приближении) от направления падения. Нейтрон выходит из вещества с равной вероятностью по любому направлению. Поэтому рассматриваемое отражение и называется диффузным.

В общем случае альбедо зависит от ядерно-физических свойств вещества, от энергии падающих нейтронов и в незначительной степени от угла падения. Особо следует отметить зависимость альбедо от соотношения между сечениями рассеяния и поглощения. Чем выше отношение сечения рассеяния к сечению поглощения, тем с большей вероятностью средний нейтрон покинет вещество. Наиболее хорошо отражают нейтроны вещества, которые используются в реакторах в качестве замедлителя и отражателя (тяжелая вода, графит, бериллий, вода). Значения альбедо таких материалов для тепловых нейтронов находятся в диапазоне 0,8 — 0,98 в случае бесконечных (в физическом смысле) размеров этих материалов. С уменьшением размеров альбедо снижается, ибо увеличивается вероятность выхода нейтронов из вещества через другую поверхность (не ту, на которую падал нейтрон). Понятно поэтому, что альбедо зависит от формы поверхности вещества.

Рассмотрим один из простейших способов экспериментального определения альбедо. Суть способа легко выяснить путем простых логических рассуждений. Пусть в однородной среде с равномерно распределенными источниками тепловых нейтронов имеется условная граница раздела, на которой помещен детектор, активируемый тепловыми нейтронами. Если доля нейтронов, поглощаемых детектором ξ < 1, то одни и те же нейтроны могут неоднократно пересекать границу раздела. Это означает, что активность детектора А0 будет

превышать значение А, которое было бы при однократном прохождении нейтронов через границу, т.к. каждое повторное прохождение будет увеличивать активность детектора. Указанное превышение зависит от доли нейтронов, поглощаемых образцом, и от альбедо исследуемой среды. Для подтверждения изложенного, будем условно считать, что нейтроны рождаются лишь с одной стороны границы, а затем многократно пересекают детектор. Определим активность, наведенную в детекторе вследствие такого многократного отражения.

При первом прохождении границы нейтроны наводят в детекторе активность А/2. Часть нейтронов, равная (1 – ξ), при этом перейдет границу раздела. Вследствие отражения от среды на детектор попадёт доля (1 – ξ)β от первоначального числа нейтронов, т. е. при вторичном прохождении нейтронов через границу в детекторе будет наведена активность A(l – ξ)β/2. После второго отражения, т.е. после третьего пересечения границы, в детекторе будет наведена активность A(1 – ξ)2β2/2 и т. д. Общая активность с учетом многократного отражения, равна сумме

A[1 + (1 – ξ)β + (1 – ξ)2β2 + …] / 2,

предел которой

A / {2[1– (1 – ξ)β]}

Так как тепловые нейтроны рождаются равномерно по объему с двух сторон границы раздела, то активность детектора

A0 = A / [1 – (1 – ξ)β]

Таким образом, альбедо β можно определить из формулы, использовав экспериментальные значения активностей А0 и А. Видно, что коэффициент l / [1– (1 – ξ)β] равен среднему числу пересечений границы раздела нейтроном в процессе диффузии. Ясно, что в эксперименте достаточно найти относительные значения активностей А0 и А.

В данной работе определяется коэффициент диффузного отражения (альбедо) тепловых нейтронов для парафина.

Описание экспериментальной установки

В работе используется метод активаций. Экспериментальная установка состоит из парафиновых блоков, источника нейтронов, активируемого детектора и счетной установки.

Парафиновые блоки выполнены в виде цилиндров и имеют следующие размеры (диаметр D, высота H): нижний – D = 60 см, Н = 30 см; верхний – D = 50 см, Н = 30 см. Плоскость между блоками является их условной границей раздела, на которой имеется паз для размещения держателя детектора. В нижнем блоке на расстоянии около 10 см от границы раздела расположен калифорниевый источник нейтронов.

В качестве активируемого образца используется природное серебро (см. табл. 3.1 в работе № 3).

Методика эксперимента

Альбедо определяется способом, суть которого изложена выше. Однако условия эксперимента отличаются от условий, принятых при теоретическом рассмотрении способа. Эти отличия перечислены ниже.

1)В работе используется точечный источник быстрых нейтронов, вследствие чего детектор активируется как тепловыми, так и резонансными нейтронами, а также существует пространственная зависимость потока тепловых нейтронов.

2)Площадь образца много меньше площади границы раздела парафиновых блоков и соизмерима с квадратом длины диффузии тепловых нейтронов в парафине.

Из этих особенностей экспериментальной установки следует, что определение альбедо прямыми измерениями А0 и А с последующим использованием формулы становится неправомерным.

Для приведения первого условия эксперимента в соответствии с условием при теоретическом рассмотрении (в парафине есть лишь равномерно распределенные по объему тепловые нейтроны) необходимо провести четыре

опыта (рис. 1).

Впервом — детектор расположен между двумя кадмиевыми пластинами и многократно активируется резонансными (надкадмиевыми) нейтронами из обоих блоков парафина.

Во втором — детектор закрыт кадмиевой пластиной со стороны нижнего, более богатого нейтронами блока. Активация в этом опыте обусловлена многократным прохождением резонансных нейтронов из обоих блоков и однократным прохождением тепловых нейтронов, попадающих на детектор со стороны верхнего блока парафина.

Втретьем — кадмиевая пластина закрывает детектор со стороны верхнего блока. В этом опыте образец активируется многократно проходящими резонансными нейтронами из обоих блоков и однократно проходящими тепловыми нейтронами из нижнего блока.

Вчетвертом — детектор активируется без кадмиевых пластин и активация его обусловлена многократным прохождением через детектор как резонансных, так и тепловых нейтронов из обоих блоков.

Несложный анализ результатов опытов показывает, что всегда условия для резонансных нейтронов остаются практически неизменными. Это позволяет исключить вклад резонансных (надкадмиевыми) нейтронов в активность образца во втором, третьем, четвертом опытах при вычитании из результатов этих опытов результата первого опыта.

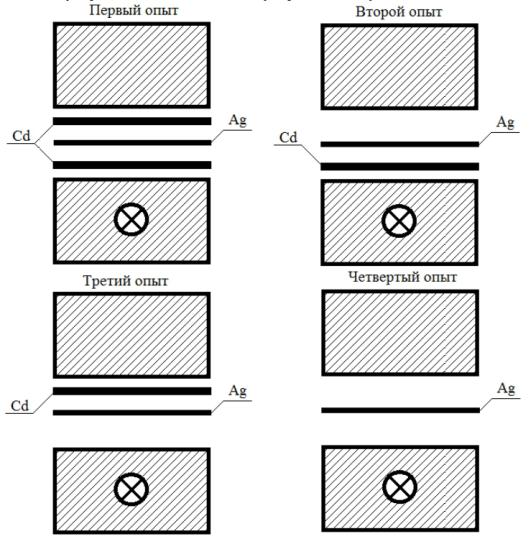
Рис. 1.

Второй и третий опыты проводятся для того, чтобы учесть (исключить) влияние пространственной зависимости потока тепловых нейтронов. Для получения активности детектора, обусловленной однократным и односторонним прохождением тепловых нейтронов, необходимо рассчитать среднее арифметическое значение результатов второго и третьего опытов (предварительно исключив вклад резонансных нейтронов).

Таким образом, проведение описанных выше четырех опытов позволяет получить такие значения активностей А0 и А (в относительных единицах), которые можно использовать для вычисления альбедо по формуле в случае, если детектор и кадмиевые пластины занимают всю границу раздела между блоками парафина (или по крайней мере достаточно большую ее часть).

Вэксперименте используются детектор и кадмиевые пластины относительно малых размеров. Это приводит к следующему:

а) значение активности А, полученное по результатам первого, второго и третьего опытов, выше теоретического значения за счет вклада тех тепловых нейтронов, которые многократно пересекают границу раздела, обходя кадмиевую пластину, прежде чем попадут на детектор с незакадмированной стороны;

б) значение активности А0, полученное по результатам первого и четвертого опытов, выше теоретического за счет вклада тех тепловых нейтронов, которые многократно пересекают границу раздела, сначала обходя детектор, затем попадая в него. Следует отметить также увеличение экспериментальных значений А0 и А по сравнению с теоретическими за счет вклада тех тепловых нейтронов, которые образуются вследствие замедления резонансных нейтронов, многократно пересекающих границу раздела. Последний эффект, однако, гораздо слабее первого.

Положение усугубляется и тем, что в различных опытах искажение (выедание) поля тепловых нейтронов в области расположения детектора различно. В одном из опытов (четвертом) на границе раздела расположен лишь детектор (доля тепловых нейтронов, поглощаемых детектором, существенно меньше единицы), в других (во втором и третьем) имеются детектор и кадмиевый экран (доля тепловых нейтронов, поглощаемых экраном, практически равна единице). Это означает, что активность А обусловлена меньшим потоком тепловых нейтронов, чем активность А0.

Врезультате отклонения экспериментальных значений активностей от теоретических ∆А и ∆А0 непропорциональны (∆А > ∆А0), что приводит к завышению альбедо.

Влияние рассмотренных эффектов зависит от размеров детектора и кадмиевого экрана. Для конкретного эксперимента можно искусственно скомпенсировать увеличение альбедо путем замены в формуле истинного значения величины ξ на подгоночное. Последнее определяется при проведении предварительного эксперимента в среде с известным значением β. В данной

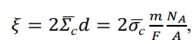
работе используется истинное значение ξ, а не подгоночное.

Истинное значение доли тепловых нейтронов, поглощаемых детектором, определяется как отношение числа поглощенных нейтронов к числу падающих на детектор. Следует только учесть тот факт, что в случае облучения детектора диффузным потоком эффективная толщина детектора в 2 раза больше геометрической, т.е. выражение для ξ имеет вид

где ∑с(σ̅с) – среднее макроскопическое (микроскопическое) сечение радиационного захвата для природного серебра (σ̅с = 50 ∙ 10 -28 м2); m – масса детектора; F – площадь детектора; NА – число Авогадро; А – массовое число серебра.

Таким образом, экспериментальная часть работы состоит в последовательном проведении первого – четвертого опытов.

При выборе временного режима работы следует обратить особое внимание на время переноса детектора из парафина к счетчику и высвечивания перед последующим опытом. Время облучения детектора выбирается таким, чтобы активность по обоим изотопам была близка к максимальному значению. Время переноса к счетчику берется по возможности малым, но не настолько, чтобы погрешность его определения давала большую погрешность в показаниях приборов за счет короткоживущего изотопа серебра. Время счета должно быть достаточным для набора хорошей статистики. Время высвечивания выбирается так, чтобы остаточная активность не искажала результат последующего опыта.

Рекомендуемый режим работы следующий: время облучения — 10 мин; время переноса образца к счетчику —15 с; время счета — 100 с; время высвечивания — 10 мин.

Особо тщательно необходимо следить за точностью соблюдения во всех опытах времен переноса и счета.

Для проверки правильности выбора времени высвечивания необходимо в течение последних 100 с при проведении высвечивания производить счет остаточной активности. Результат следует учесть при обработке экспериментальных данных.

Работа должна проводиться в следующей последовательности.

1)подготовить НИУ «РАиНИ» к работе (Приложение 1);

2)измерить фон (3 раза длительностью по 100 с);

3)провести последовательно опыты с первого по четвертый; данные занести в таблицу;

4)записать данные детектора;

5)показать результаты измерений преподавателю.

Таблица измерений

Измерение фона:

Массогабаритные параметры детектора: Масса: [г] Диаметр: [мм]

Измеренные значения:

Значение

Измеренная остаточная активность:

Значение