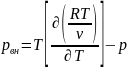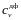Обработка экспериментальных данных

1. Построить в масштабе (формат А4) в р,t-координатах кривую насыщения воды, экспериментальные точки и две сглаженные изохоры, построенные как результат аппроксимации результатов измерений. Для более точной аппроксимации в области пересечения изохор с линией насыщения параметры (р и t) в точках а и b (см. рис. 5.2.2) определяются по таблицам [8] по итоговым значениям удельного объема, найденным в п.2.

2. Определить величину удельного объёма для каждой изохоры. Значение удельного объёма находится из данных проведенного эксперимента с помощью таблиц [8]. Для определения удельного объёма необходимо выбрать на изохоре в однофазной области точку вдали от кривой насыщения и определить удельный объём в этом состоянии по таблицам (по давлению и температуре). Для повышения точности повторить эту процедуру, взяв несколько различных точек на изохоре (но не вблизи кривой насыщения, где неравновесность процесса нагревания оказывает большее влияние на результат эксперимента). Итоговое значение удельного объема для каждой изохоры (v_a и v_b) рассчитывается как среднеарифметическая величина.

3. Определить суммарную массу воды и водяного пара в каждом сосуде установки (m_a и m_b), имея в виду, что объём каждого сосуда равен V = 300 cм³:

m = V / v.

4. Рассчитать степень сухости водяного пара в точках 1а и 1b (рис. 5.2.2) на начальных участках изохор по температурам (или по давлениям), указанным преподавателем. Для этого воспользоваться формулами для влажного пара, таблицами водяного пара [8] и полученными в п.2 значениями удельных объёмов на двух изохорах

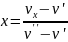
(5.2.1)

5. Рассчитать количество теплоты, необходимое для нагрева воды и водяного пара в одной из экспериментально исследованных изохор от состояния 1а (или 1b) до состояния 2а (или 2б), указанного преподавателем:

(5.2.2)

где u - удельная внутренняя энергия, определяемая по формуле

в которой удельная энтальпия водяного пара в начале процесса (h_1a или h_1b) рассчитывается по формулам для влажного пара

h1 = h’ + x(h” – h’)

(5.2.3)

a в конце процесса (h_2a или h_2b) берётся из таблиц [8]. Значение удельного объёма в формуле (2) взять из п.2.

6. Рассчитать величину внутреннего давления, обусловленного силами взаимодействия молекул вещества.

а) для одного термодинамического состояния на экспериментальных изохорах вдали от кривой насыщения (состояние указывает преподаватель):

(5.2.4)

Производная (∂p/∂T)_v в заданной точке изохоры определяется графически на р,Т- диаграмме, как тангенс угла наклона касательной, проведенной к изохоре в заданной точке: tgα = ∆p/∆T, где ∆p и ∆T – катеты прямоугольного треугольника, гипотенуза которого совпадает с построенной касательной.

б) Определить, какова была бы величина внутреннего давления, если бы вода и водяной пар подчинялись уравнению Ван-дер-Ваальса:

(5.2.5)

Константы a и b уравнения Ван-дер-Ваальса для воды приводятся в табл.5.2.2. Известно, что постоянные a и b уравнения Ван-дер-Ваальса не определяются однозначно из критических условий. В зависимости от выбора определяющих параметров (p_кр, v_кр, T_кр) получаются различные константы a и b (см. табл. 5.2.2).

Таблица 5.2.2

Константы уравнения Ван-дер-Ваальса для воды

Определяющие параметры	а, Н·м4/кг2	b, м3/кг
pкр, Tкр	1705	0,001692
vкр, Tкр	1043	0,001035
pкр, vкр	638	0,001035

Таким образом, в формуле (5.2.5) можно взять любое из трёх значений константы а. Чаще берут величину а, полученную по известным параметрам p_кр и T_кр.

в) Определить внутреннее давление идеального газа, используя (5.2.4) и уравнение состояния идеального газа – уравнение Клапейрона - Менделеева ,

5.2.6

Сравнить все три полученных значения внутреннего давления.

7. Рассчитать удельную изохорную теплоемкость c_v воды, влажного и перегретого водяного пара. С этой целью на изохорах, исследованных в эксперименте, выделяются процессы, указанные преподавателем, для которых рассчитываются средние (в заданном интервале температур) теплоемкости по формуле

cv = ∆u /∆T

(5.2.7)

в которой ∆Т и ∆u – изменения температуры и удельной внутренней энергии в указанных преподавателем изохорных процессах.

Предлагается определить изохорные теплоемкости по обе стороны левой или правой пограничных кривых, где наблюдается скачок изохорной теплоемкости при переходе из двухфазного состояния влажного пара в однофазное состояние воды или перегретого пара. Для этого на изохоре 1а-2а выделяются два процесса 1а-а и а-2а (рис.2), а на изохоре 1b-2b процессы 1b -b и b-2b. Температура, давление и удельная энтальпия на пограничных кривых в точках а и b определяются по найденным в п.2 значениям удельного объема с помощью таблиц [8]. Преподавателем задаются температуры (или давления) в состояниях 1а (или 1b) на 20÷30°С меньше, чем температуры t_a (или t_b); а в состоянии 2a (или 2b) на 20÷30°С больше, чем температура воды t_a (или температура сухого насыщенного пара t_b). Заданные параметры (р или t) в состояниях 1а, 1b, 2a, 2b отмечаются в рабочем протоколе, который подписывается преподавателем.

Необходимые для расчета с_v по формуле (5.2.7) значения удельной внутренней энергии u определяются так же, как в п.5 по формуле (5.2.2). Расcчитанные значения c_v в двухфазном состоянии влажного пара и однофазном состоянии воды (или перегретого пара ) сравнить с табличными данными, полученными с помощью программы WaterSteamPro и (или) приведенными в табл.[?].

Таблица 5.2.3

Табличные значения удельной изохорной теплоемкости

воды и водяного пара на пограничных кривых, кДж/(кг·К)

v, м3/кг 0,00108 3,57 4,28 0,00110 3,49 4,32 0,00112 3,42 4,36 0,00114 3,36 4,41 0,00116 3,31 4,45 0,00118 3,26 4,50 0,00120 3,22 4,55 0,00122 3,19 4,61

v, м3/кг 0,02 19,8 3,03 0,03 22,7 2,75 0,04 25,0 2,58 0,05 26,9 2,47 0,06 28,5 2,38 0,07 30,0 2,31 0,08 31,3 2,25 0,09 32,4 2,20

8. Оценить неопределённость одного из найденных в п.2 значения удельного объёма (указывает преподаватель).

Максимальная относительная неопределённость определения удельного объёма может вычислена по формуле:

= / =

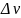Здесь 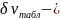относительная неопределённость табличных значений удельного объёма (её можно принять равной 0,1%, т.е. ); Δp и ΔТ — абсолютные неопределённости измерения давления и температуры принятого состояния, обусловленные как систематическими неопределённостями измерительных приборов, так и случайными погрешностями, вызванными главным образом отсутствием равновесного состояния. Целесообразно принять Δp = 0,1 МПа, ΔТ = 1÷2 К.

Производные и вычисляются с помощью таблиц [8] в виде отношения минимальных табличных разностей: 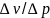и соответственно на изотерме и изобаре.