
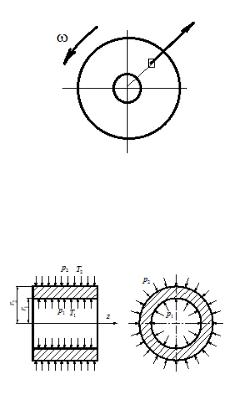
ПРИКЛАДНАЯ ФИЗИКА
Лекция 4
Осесимметричные задачи теории упругости
Рассматриваем тела вращения, нагруженные силами, симметричными оси тела. Вводим цилиндрическую систему координат. Рассматриваем плоскую задачу (напряжения и деформации зависят только от r).
Задачи:
Вращающийся диск.
Толстостенный цилиндр, нагруженный внешним и внутренним давлением. Задача Ламе.
Задача Ламе. Вывод уравнения равновесия в напряжениях
1
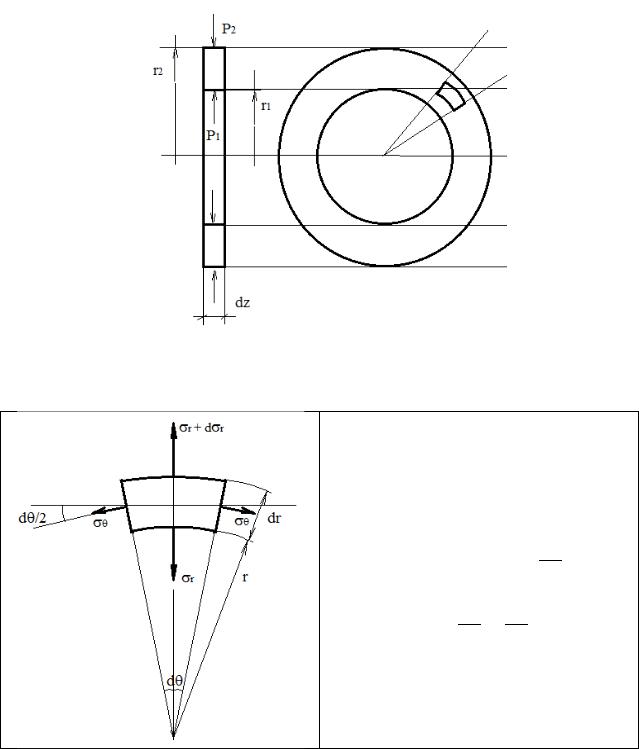
Выделим малый элемент , . Обозначим , напряжения в радиальном и окружном направлении. Составим уравнение равновесия
∑ = 0
( + )( + ) −
− − 2 2 = 0
(sin2 = 2 )
+ + + − − = 0
≈0
Получаем
|
+ |
− |
= 0 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
+ |
|
|
= |
(1) |
||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
Остальные уравнения обращаются в тождества.
2
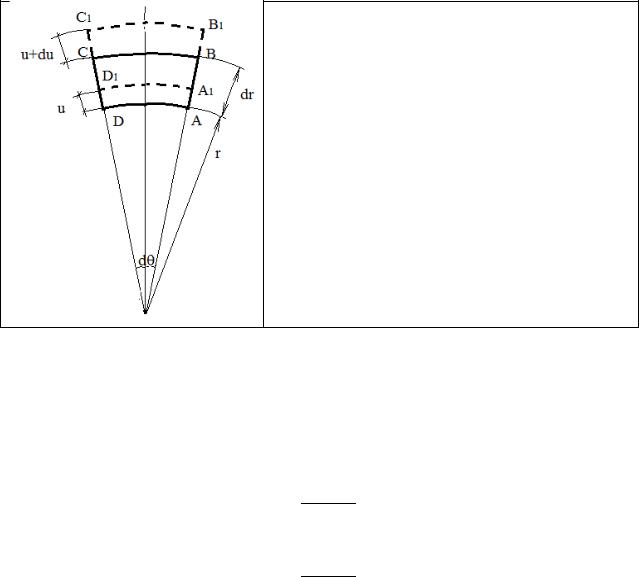
(1)– уравнение равновесия элемента в напряжениях. Неизвестных два:
( , )
Деформации в радиальном и окружном направлении
- перемещение в радиальном направлении
- относительная деформация в радиальном направлении
- относительная деформация в окружном направлении
|
|
= |
1 1 − |
= |
+ − |
= |
|
|
|
||||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||
|
= |
1 1 − |
= |
( + ) − |
= |
|
|||||||
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
= |
|
, |
|
|
= |
|
(2) |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
Уравнение равновесия в перемещениях
Обобщенный закон Гука для плоского напряженного состояния
(см. лекция 6)
= − ( + )
(3)
= − ( + )
Подставляем (2) в (3)
= |
|
( |
|
+ |
|
) |
|
|
|
||||
|
1 − 2 |
|
|
|
|
|
|
|
|
||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
( |
|
+ |
|
) |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 − 2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
и в (1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
( |
|
+ |
|
|
|
|
− |
|
|
+ |
|
( |
|
|
+ |
|
− |
|
− |
|
) ) = 0 |
|||||||||||
|
1 − 2 |
2 |
|
2 |
|
|
|
|
|
|||||||||||||||||||||||||
Уравнение равновесия в перемещениях |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
+ |
|
|
− |
= |
|
|
|
(4) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Интегрирование дифференциального уравнения в перемещениях
Перепишем уравнение в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
( |
|
|
+ |
|
|
|
) = 0, |
|
|
|
|
( |
|
|
|
|
|
|
( )) |
= 0 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Интегрируем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 |
|
|
( ) = 2С , |
|
|
|
|
|
|
|
|
|
( ) = 2С , |
|
( ) = С + |
2 |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Для определения констант интегрирования С1 |
и |
|
2 воспользуемся |
|||||||||||||||||||||||||||||||||||||||||||||
граничными условиями |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
( = ) |
= − , |
|
|
( = ) = − |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|||||||||
Запишем напряжения через перемещение |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
(С − |
2 |
|
+ |
1 |
(С + |
2 |
)) |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − 2 |
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
= |
|
|
|
|
|
|
( |
1 |
(С + |
|
2 |
) + (С − |
2 |
)) |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 − 2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Подставляем в граничные условия |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
( = ) |
= |
|
|
|
|
|
|
|
((1 + )С |
− (1 − ) |
2 |
) |
= − |
|
|
|||||||||||||||||||||||||||||||
|
|
|
1 − 2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
1 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
( = ) |
= |
|
|
|
|
|
|
|
((1 + )С |
− (1 − ) |
2 |
) |
= − |
|
|
|||||||||||||||||||||||||||||||
|
|
|
1 − 2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
2 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение системы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
1 − |
|
|
|
|
|
2 |
|
− |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
С |
= |
|
|
|
|
|
|
|
|
|
∙ |
|
1 |
1 |
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
− 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + |
|
|
|
( − |
) |
2 2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
С2 = |
|
|
|
|
|
|
|
∙ |
|
|
|
|
1 |
|
|
|
2 |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
− 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставляя в решение, получаем первую формулу Ламе |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
1 − |
|
|
|
2 |
|
− 2 |
|
|
|
1 + |
|
|
( − |
) |
2 |
2 |
1 |
||||||||||||||||||||||||||||||
( ) = С + |
2 |
|
= |
|
|
|
|
|
|
|
∙ |
|
1 |
1 |
|
|
|
|
|
|
|
2 |
2 |
|
+ |
|
|
|
|
|
|
|
∙ |
|
|
|
1 |
2 |
1 |
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
2 |
− 2 |
|
|
|
|
|
|
|
|
|
2 |
− 2 |
|
|
|
|
||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
||||
Напряжения определяются по второй формуле Ламе |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
− 2 |
|
|
|
|
|
( − |
) 2 |
2 |
1 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
= |
|
1 |
1 |
|
|
|
|
2 |
|
2 |
|
|
− |
|
|
|
1 |
|
|
|
2 |
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
2 |
− 2 |
|
|
|
|
|
|
|
|
|
2 |
− 2 |
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
2 |
− 2 |
|
|
|
|
|
( − |
) 2 |
2 |
1 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
= |
|
1 |
1 |
|
|
|
|
2 |
|
2 |
|
|
+ |
|
|
|
1 |
|
|
|
2 |
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
2 |
− 2 |
|
|
|
|
|
|
|
|
|
2 |
− 2 |
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Обычно две формулы объединяют |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
( |
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
, = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
− |
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
заметим, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
5
