4. Расчет трубной доски

В качестве расчетной схемы принимается круговая (кольцевая) пластина постоянной толщины h, находящаяся под действием заданной внешней нагрузки.

4.1. Получить выражения для радиального Мr и окружного Мθ изгибающих моментов и построить соответствующие эпюры (относительно параметра внешней нагрузки).

4.2. Определить допускаемое значение внешней нагрузки. Построить эпюру прогибов пластинки при нагрузке, равной ее допускаемому значению.

Указание. Материал пластинки - легированная сталь (марку стали выбрать самостоятельно).

При вычислениях принять Е = 200 ГПа; μ= 0.3, [σ]= 240 МПа. Критерий прочности выбирается самостоятельно.

№ Варианта	, м	, м	, м
25	0,30	1,2	0,08

Рисунок 4.1. Исходная схема

4.1. Получить выражения для радиального Мr и окружного Мθ изгибающих моментов и построить соответствующие эпюры (относительно параметра внешней нагрузки).

Дифференциальное уравнение осесимметричного изгиба пластин:

(4.1)

или

(4.2)

где – оператор Лапласа

ГУ:

(4.3)

Решение ищем в виде:

(4.4)

Находим неизвестные константы подставляя граничные условия (4.3) в уравнение (4.4):

(4.5)

Формулы для радиальных и окружных моментов:

(4.5)

4.2. Определить допускаемое значение внешней нагрузки. Построить эпюру прогибов пластинки при нагрузке, равной ее допускаемому значению.

Рассмотрим два опасных сечений:

При

При

Найдем напряжения:

При

При

По критерию Сен-Венана:

При

При

Опасное сечение при .

Найдем допускаемое значение внешней нагрузки

Построим эпюры

Рисунок 4.2. Эпюра прогиба, м

Рисунок 4.3. Эпюра радиального момента, Па

Рисунок 4.4. Эпюра окружного момента, Па

5. Расчет патрубка корпуса подогревателя

В качестве расчетной схемы принимается круговая цилиндрическая оболочка постоянной толщины h, нагруженная осесимметричной нагрузкой.

5.1. Получить аналитические выражения и построить эпюры внутренних силовых факторов .

5.2. Определить толщину оболочки h из условия прочности.

5.3. Построить эпюру нормального прогиба w(x) для оболочки толщиной h,

найденной в п.5.2.

Указание. Вычисления для w(x), Мx, Мy, и y N проводить с шагом , , где - длина полуволны краевого эффекта.

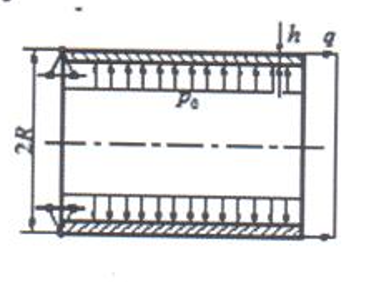
№ Варианта
25	0,07	0,90	3	0,85	0,25

5.1. Получить аналитические выражения и построить эпюры внутренних силовых факторов .

Дифференциальное уравнение осесимметричного изгиба круговой цилиндрической оболочки:

(5.1)

Решение дифференциального уравнения (5.1) ищем в виде суммы однородного и частного решений:

_(5.2)

Для решения однородной части уравнения:

_(5.3)

Введем обозначение

_(5.4)

где k – волновое число.

Уравнение имеет вид:

_(5.5)

ему соответствует характеристическое уравнение

_(5.6)

которое имеет 4 корня .

Учитывая, что и имеем

_(5.7)

Однородное решение имеет вид:

_(5.8)

Другая форма записи:

_(5.9)

или

_(5.10)

При

_(5.11)

Решение примет вид

_(5.12)

Частное решение имеет вид:

_(5.13)

_(5.14)

_(5.15)

_{Общее решение имеет вид:}

_(5.16)

Граничные условия при :

_(5.17)

_{Подставляя граничные условия (5.17) в решение (5.16), находим неизвестные константы , полагая h=1.}

_(5.18)

_{С помощью формул (5.18) находим усилия и строим эпюры.}

_{Для построения эпюр посчитаем зону краевого эффекта:}

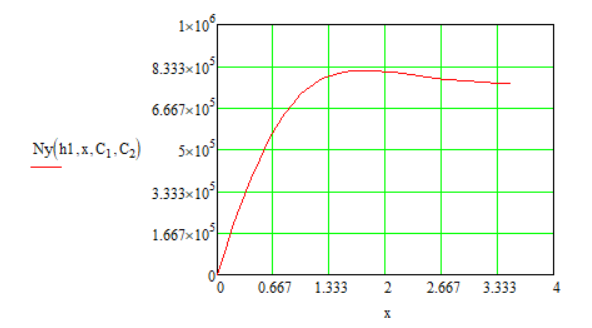
Рисунок 5.1. Эпюра , Па

Рисунок 5.2. Эпюра , Па

Рисунок 5.3. Эпюра , Па

_(5.19)

5.2. Определить толщину оболочки h из условия прочности.

_{Опасное сечение при x=0.58}

_{По критерию Сен-Венан найдем эквивалентные напряжения}

_{Из условия прочности найдем толщину оболочки}