
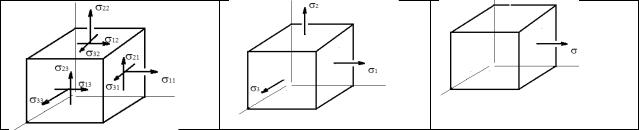
ПРИКЛАДНАЯ ФИЗИКА Лекция 15
Основы теории прочности
Задачи теории прочности – найти значения напряжений, при которых в заданной точке нагруженного тела наступает предельное состояние.
Под предельным состоянием понимаем:
Для пластичного материала – появление пластических деформаций
[ ] = [ Т]
Для хрупкого материала состояние предшествующее хрупкому
разрушению |
|
|
Т |
|
в |
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
[ ] = [ ] [ ] |
|
||||
Для хрупко-пластичного материала |
[ |
] |
0,2 |
|
|||||
|
|
|
|
|
|
[ ] |
|
||
[ ] |
- нормативный коэффициент запаса |
прочности= |
. |
||||||
вр |
вс |
0,2 |
- определяются из опытов на растяжение. |
||||||
Т |
|
|
|
|
|
|
|||
Эквивалентное напряжение |
- напряжение, которое нужно создать в |
||||||||
, |
|
, , |
|
|
|||||
экв
растянутом образце, чтобы его напряженное состояние было равноопасно исходному.
Условие прочности |
экв = ( , , ) < [ ] |
Опыты Бриджмена |
При всестороннем равномерном сжатии пластических деформаций нет.
1

Критерий текучести Сен-Венана
(критерий наибольших касательных напряжений)
Текучесть наступает тогда, когда наибольшие касательные напряжения достигают предельного значения, не зависящего от вида напряженного
состояния, а зависящего только от свойств материала. |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
Т |
|
|
|
|
на площадке |
|
, |
|||
Для одноосного напряженного состояния |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
< |
|
|
= 2 |
|
|
45° |
|
|||
условие прочности |
= 2 < [2] |
|
|
|
|
|
|
|
|
|
||||||||
В случае объемного напряженного состояния = |
1−2 3 |
(лекция 4). |
||||||||||||||||
|
1−2 3 < [2] |
|
= |
|
1 |
− 3 < [ ] |
|
|
|
|
||||||||
Условие прочности по Сен-Венану |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
экв |
= |
|
− |
|
|
|
|
|
|
|
|
||||
|
|
|
|
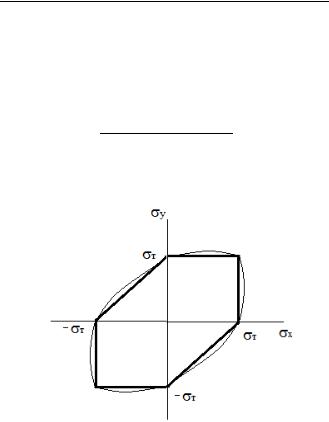
Геометрическая иллюстрация для |
|
|||||||||||||
|
|
|
|
|
|
< |
[ ] |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
плоского напряженного состояния |
|
|||||||||
|
|
|
|
|
|
|
|
Участок I: |
= 0 |
> |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
напряжение |
|||||
|
|
|
|
|
|
эквивалентное |
|
> 0, > 0, |
||||||||||
Условие прочности |
< Т |
|
|
|
экв |
= |
− = |
|
|
|||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
Участок II: |
|
|
> эквивалентное напряжение |
||
> 0, > 0, |
|||||
|
= |
− |
= |
|
|
экв |
|
|
|
|
|
Условие прочности |
< Т |
||||
Участок III: |
|
||||
|
= |
|
|
|
> 0, < 0 эквивалентное напряжение |
||||
экв |
|
− |
− < Т |
|
Условие прочности |
||||
|
||||
Область допустимых значений находится внутри замкнутой границы I- II-III-...
Очевидные недостатки критерия Сен-Венана: Граница области допустимых значений не гладкая. В критерий не входит 2.
Критерий текучести Мизеса (Губера-Мизеса)
Текучесть наступает тогда, когда плотность потенциальной энергии изменения формы достигает предельного значения, не зависящего от вида напряженного состояния, а зависящего только от свойств материала.
1 |
|
1 |
|
Плотность потенциальной энергии u на примере растяжения |
|||
= 2 |
|
∙ = 2 |
|
|
|
1 |
|
|
= |
= 2 |
|
Рассмотрим общий случай нагружения для главных площадок
3

|
1 |
|
1 |
|
|
2 |
|
= 1 1 1 |
+ |
1 2 |
2 + 1 |
3 3 = |
|
|
3 |
|
2 |
|
1 |
|
||||||||||
= |
1 |
− |
− |
3 |
2 |
|
2 |
2 |
|
1 |
2 |
|
3 |
+ 3 |
|
− |
− |
|
||||||||||||
2 |
|
|
|
+ 2 |
|
− |
|
− |
|
|
|
|
||||||||||||||||||
|
( |
|
|
|
|
|
|
|
|
|
1 |
= |
1 |
− |
2 − 3 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
Вспоминаем закон Гука, Лекция 6 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
= |
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
2 |
− 1 |
3 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
= |
3 |
|
|
1 |
− |
2 |
|
|
|
|
|
|
|
|
|
|||
|
) |
|
|
= 1 |
|
|
|
|
− |
|
|
|
|
3)] |
|
|
|
|
||||||||||||
|
|
|
|
[ 12 + 22 + 32 −2 ( 1 2 |
|
+ 1 3 + 2 |
|
|
|
|
||||||||||||||||||||
|
Это полная |
плотность потенциальной энергии. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Найдем энергию изменения объема1 |
|
+ 2 |
+ 3) |
- среднее напряжение |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
( |
|
= 3 ( 1 |
|
|
|
|
– |
отвечает за |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
гидростатическое |
|
давление) |
|
|
|
|
|
||||||||||||
изменение объема.
Пусть |
= 1 = 2 = 3 |
|
|
|
|
|
|
|
|
|
|
|
||||
Плотность потенциальной энергии изменения объема . |
|
|
|
|||||||||||||
3 |
|
3 |
|
|
= |
3(1 −2 ) |
|
2 |
= |
3(1 −2 ) 1 |
+ 2 |
2 |
= |
|||
= 2 |
= 2 −2 |
2 |
2 |
|
2 |
3 ( 1 |
+ 3) |
|||||||||
|
|
= |
(1 −2 ) |
2 |
|
|
2 |
|
|
|
2 + 1 3 |
+ 2 3)] |
|
|
||
|
|
6 |
[ 1 |
|
+ 2 |
+ 34+ 2( 1 |
|
|
||||||||
Плотность потенциальной энергии изменения формы |
3] |
|||||||||||||||
|
= − |
= 1 + [ 12 |
+ 22 + 32−1 |
2 − 1 3 − 2 |
||||||||||||
Другая форма записи |
3 |
− 2)2 + ( 1 − 3)2 |
+ ( 2 − 3)2] |
|
||||||||||||
|
= 1 + [( 1 |
|
|
|||||||||||||
Для растяжения |
6( |
|
|
|
2 = 3 |
= 0, 1 = |
|
|||||||||
В общем |
|
= |
|
|
< |
|
|
[ ] |
|
|
|
|
|
|||
|
|
сжатия) |
|
|
3 |
|
2 |
|
|
|
|
|||||
|
|
3 |
|
|
2 |
|
|
- условие прочности |
||||||||
|
|
|
|
1+ |
|
|
|
1+ |
|
|
||||||
|
случае нагружения условие прочности |
|
||||||||||||||
= 1 + [ 12 + 22 |
+ 32 |
−1 |
2 − 1 3 − 2 3] < 1 + [ ]2 |
|||||||||||||
Условие |
3 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
||
|
прочности по критерию Мизеса |
|
|
|
||||||||||||
экв = |
|
+ |
+ |
− |
− − |
< |
[ ] |
|||||||||
Геометрическая иллюстрация для=плоского0 напряженного состояния
экв = 2 + 2−, <
5
Критерий хрупкого разрушения (Критерий Мора)
Для хрупких материалов условие прочности при растяжении и сжатии
имеют разный вид растяжение – < [ вр] сжатие – < [ вс]
|
|
|
экв = − < [ р] |
|
|
|
|||||||
Критерий Мора (без вывода) |
|
|
|
|
|
|
|
|
|
||||
|
[ р] = |
[ ] , = в , = [ ] |
|
|
|
|
|
|
|
|
|
||
Здесь |
|
вр |
вр |
[ р] |
= 1 |
< [ |
|
] |
|
|
|
||
при сжатии – |
|
|
экв |
р |
|
|
|
||||||
Получаем при растяжении – |
|
|
|
|
|
|
|
|
|
||||
|
экв = 3 |
[ р] |
3 < [ |
р |
] |
=> 3 |
< [ |
|
] |
||||
|
= [ ] |
|
|
||||||||||
Для пластичных материалов m=1, получаем критерий Сен-Венана.
6
