
ПРИКЛАДНАЯ ФИЗИКА Лекция 8
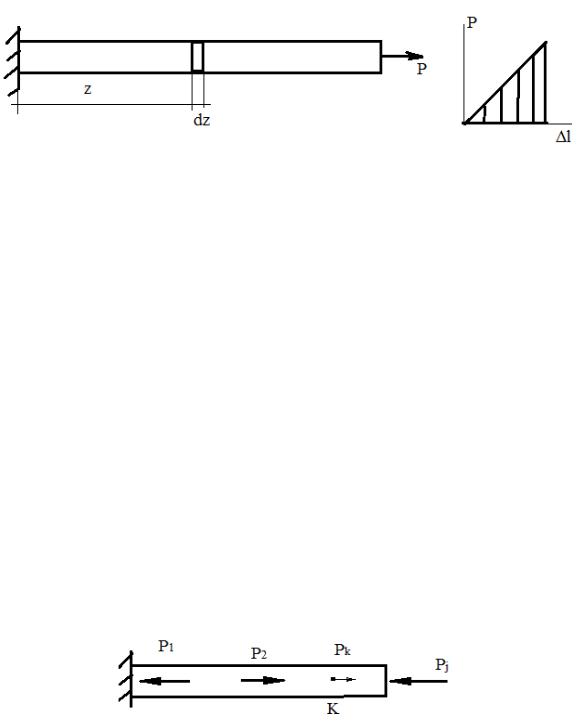
Потенциальная энергия упругой деформации при растяжениисжатии
2
Внешние нагрузки прикладываются квазистатически. Потерями на трение пренебрегаем.
Для малого элемента |
1 |
|
1 |
|
1 |
2 |
|
||||
|
энергия |
|
|
||||||||
Полная |
|
2 |
∆( ) = 2 |
|
|
= 2 |
|
||||
= = |
|||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
= = 1 |
|
|
|
|
|
||||
|
|
|
|
|
|
||||||
|
|
|
|
0 |
2 |
0 |
|
|
|
|
|
Интеграл Максвелла – Мора ∆
Задача: Определить перемещение( = 1,2,3,к точки. . , )К под действием сил
I.До приложения внешних нагрузок приложим в точке К служебную силу К. Потенциальная энергия
1

|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 = |
1 |
|
2 |
|
|
|
|
|
|||||||
II. |
|
Не снимая |
К |
, |
|
|
∆к |
|
|
|
|
2 |
0 |
|
|
|
|
|
|
|
|||||||||
|
|
|
приложим внешние нагрузки |
|
, при этом точка К |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 = |
1 |
|
2 |
|
|
|
|
|
|||||||
|
|
|
переместится на (то что мы ищем). Работа сил |
|
|
||||||||||||||||||||||||
|
|
|
|
= 1 |
+ 2 |
|
|
|
2 0 |
|
|
|
|
|
+ К∆К |
||||||||||||||
|
|
|
|
+ К∆К= 1 |
2 + 1 2 |
||||||||||||||||||||||||
|
|
|
при этом сила К |
совершает работу |
К∆К. Полная энергия |
||||||||||||||||||||||||
|
|
|
= 1 |
|
( |
+ )2 |
|
2 0 |
|
|
|
|
|
2 0 |
|
|
|||||||||||||
III. |
|
= 1 |
|
2 + 1 |
2 + |
||||||||||||||||||||||||
|
С другой стороны |
|
|
2 0 |
|
|
|
|
2 0 |
|
|
|
|||||||||||||||||
|
|
|
|
2 0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|||||||||||||
|
|
|
Сравнивая II , |
|
III |
|
|
К∆К= |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||||
силы |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
К |
, где |
|
|
- продольная сила в стержнях от единичной |
|||||||||||||||||||||
Пусть |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
приложенной в точке К ( |
К = 1 |
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∆К= |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 1,2,3, … , ) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
, , , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
Интеграл (формула) Максвелла – Мора |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
∆К= |
|
|
|
|
|
|
|
|
|
|||||||||||
Если |
|
|
|
|
постоянны в пределах i – го участка ( |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
2 |
|
|
|
|
|
|
|
|
|
|||||
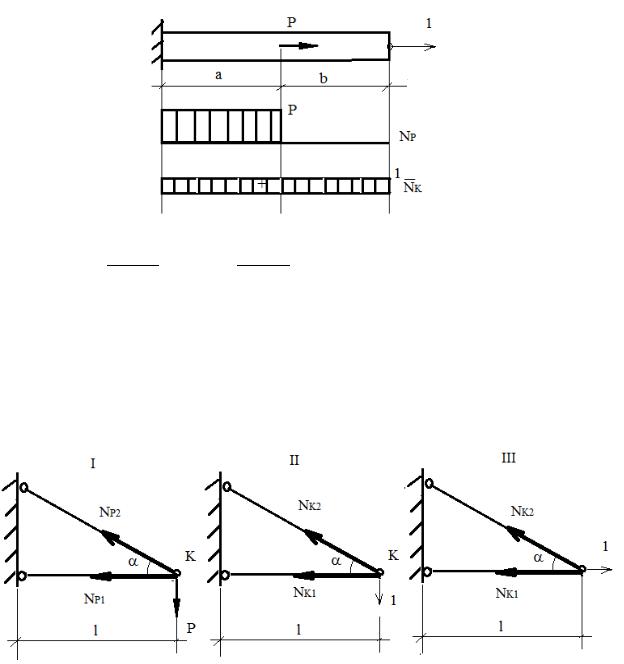
Пример 1
∆К= = 2 = 1 ∙ ∙ + 1 ∙ 0 ∙ =
=1 =1
Пример 2
Найти:
1.Вертикальное перемещение точки К
2.Горизонтальное перемещение точки К
∑ = 0 |
1 |
+ 2 cos = 0 |
|
||
1. По схеме I найдем продольную силу в первом и втором стержне |
|||||
∑ = 0 |
2 |
sin − = 0 |
|
|
|
|
1 = − |
cos |
, |
||
Имеем |
|
|
|
|
|
Приложим единичную силу в точке К в вертикальном направлении По схеме II найдем продольную силу в первом и втором стержне
3
|
|
|
|
|
|
|
К1 |
|
|
|
|
cos |
|
|
|
|
|
К2 |
|
|
|
1 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
= − sin , |
|
|
|
|
= sin |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
Определяем по формуле Максвелла – Мора вертикальное перемещение |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
cos = |
|||||||||||||||||
т. К |
∆К= |
|
= |
|
|
= |
|
|
|
К2 |
|
2 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
К1 1 |
|
|
|
|
|
|
|
||||||
|
=1 |
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||||||
|
|
|
1 |
|
|
|
cos |
− |
cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
= |
− sin |
sin |
|
+ sin sin cos = |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
= |
|
|
1 + cos2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
sin2 cos |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
2. Аналогично находим горизонтальное перемещение точки К |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= 1, |
|
|
|
|
|
|
|
|
= 0 |
|
|
|
|
|
|
|
|||||
|
По схеме III |
|
|
|
|
|
|
|
К1 |
|
|
|
|
|
|
|
К2 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
К |
|
|
|
|
|
|
|
|
|
cos |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
∆ |
= |
|
|
+ |
К2 |
|
|
2 |
= |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
К1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
cos |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|||||||
|
|
|
|
= 1 − |
sin |
|
+ 0 sin cos |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
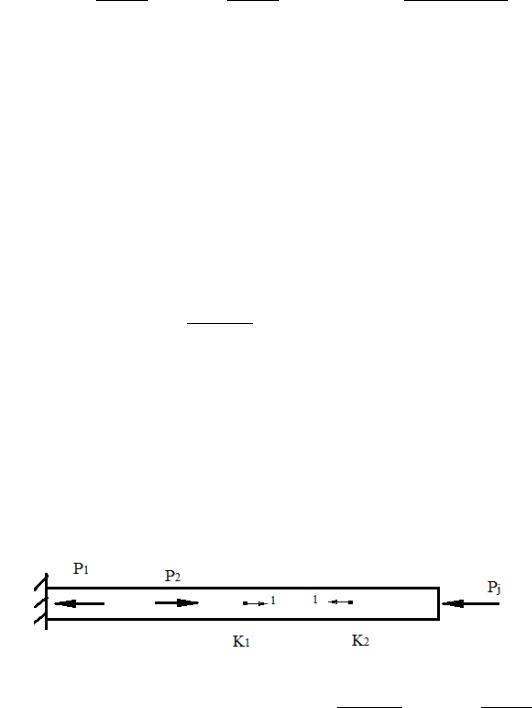
Определение взаимного перемещения сечений
∆1 2= ∆ 1 + ∆ 1= + =
=1 =1 =1
- продольная сила от первой единичной силы
4
- продольная сила от второй единичной силы- от двух единичных сил.
5
