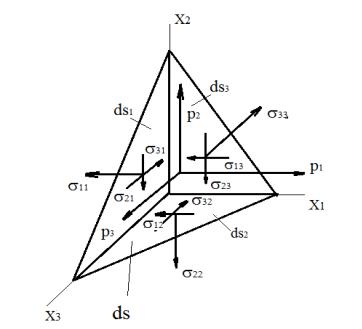
3 семестр / Лекции / ПРИКЛАДНАЯ ФИЗИКА-1-4

На площадках 1, 2 3 задан

12

13

11

=

21

22

23

31

32

33

.

= ( 1, 2, 3)

нормаль к

,

найдем

̅= ( 1

, 2

, 3)

площадке

на

Уравнения равновесия

1

= 0

1

− 11

− 13 3 = 0

Из геометрии

1 − 12

2

Получаем

1

= 1,

2 = 2

,

3 = 3

1

= 11

1

+ 12 2

+ 13

3

(1)

2

= 21

1

+ 22

2

+ 23

3

3

= 31

1

+ 32

2

+ 33

3

Или

=

напряжения на ней отсутствуют

Главные напряжения и главные площадки

Поставим задачу – найти такое

(такую площадку ), что касательные

Из формул Коши 1)

=

̅= ,

,

=

,

=

1

1

2

2

3

3

( 11 − ) 1 + 12 2

+ 13

3

= 0

21

получаем

− ) 2

+ 23

3

= 0

Или в матричном

1

+

( 22

+

2

+

(

− )

= 0

31

1

32

33

3

11 −

12

13

1

виде

22 −

23

2

21

31

11

32

33

−

3 = 0

(2)

−

12

13

Это проблема

собственных значений

21

22 −

23

= 0

31

32

33

−

(3)

Где

3

− 1 2

+ 2 − 3

= 0

1

= 11

+ 22

+ 33

2

2

= 1121

1222 + 1131

1333 + 3222

3323

11

12

13

3

=

21

22

23

31

32

33

нумеруем

1, 2

это

, 3

Главные напряжения. В дальнейшем

(2) или (3) имеет 3 корня

площадки.

1

2

3

( = 1,2,3)

(это важно!)

≥

Каждому

соответствует

, которые определяют Главные

≥

Пусть мы нашли . Для нахождения имеем три уравнения

11

−

1

+ 12

2

+ 13

3

= 0

Поскольку

21

1

+

22

− 2

+ 23

3

= 0

+

+

−

= 0

31

1

32 2

33

3

определитель системы равен нулю, три уравнения линейно

зависимы. Решаем любые два полагая, например, 1

= 1.

=

1, 2, 3

+ 22 + 23 = 1

Обычно добавляют условие нормировки

21

При этом ∙ = 0, ≠ .

это значит,

что

3

−

2

+

− = 0

координат.

1, 2

, 3

1

2

3

инвариантны по отношению к преобразованию

Если выбрать координатные оси, для которых площадки являются

главными, также получим (3)

2

+ 02 − 03

= 0

3

− 01

1

0

1

0

01

= 1

+ 2 + 3

2

0

0

=

02 = 0

2

+

0 3

+1

0

3

0 1 2 + 1 3 + 2 3

03

= 0

2

0

= 1

2 3

0

0

3

, 3 = 03

1 = 01, 2 = 02

0

11

12

0

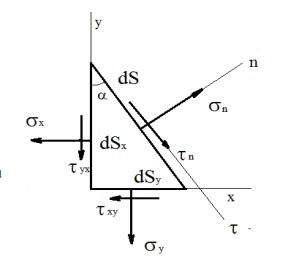
Плоское напряженное состояние

=

0

= 21

22

0

0

0

0

0

0

0

=

cos , = sin

−

cos −

sin −

sin −

cos = 0

Получаем

=

cos2 + sin2 + sin 2 = 0

(4)

−

sin +

= 0

cos −

sin = 0

cos +

Получаем

sin cos − cos2 + sin2

= sin cos −

= −2

sin 2 − cos 2

(5)

Теперь из (5) найдем такое , что

= 0

(6)

значения

2 = 2

−

,

при котором

принимает

экстремальные

Теперь из (4) найдем

= −2 cos sin + 2 cos sin + 2

cos 2 = 0

2 = 2

Получаем

, то есть

совпадает с (6).

На главных площадках

= 0 и

=

= 1

, = 2, = 0

Еще одна задача: Рассмотрим главные площадки

и найдем для которого = . Из (5)

1 − 3

= 1 −2 3

sin 2

= 2

2

2 = 0

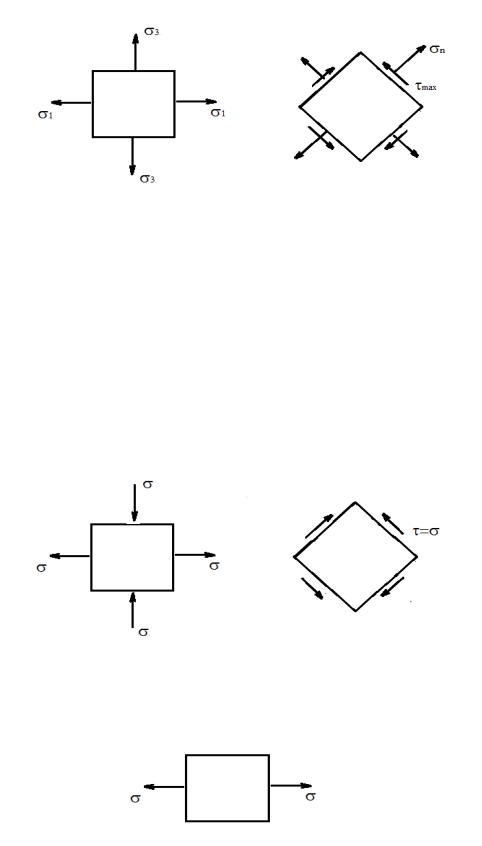
Для площадки

касательные напряжения принимают

максимальное значение

1

= 4

1

− 3

при этом

= 1+2 3

=

2

1

= −3 = (чистый сдвиг)

Два частных случая: 1.

2. 3 = 0

= 1−2 3 = , = 1+2 3 = 0

(растяжение-сжатие)