Файловый архив студентов. Файловый архив студентов.
1284 вуза, 4929 предмета.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Национальный исследовательский университет «МЭИ»
Предмет:
Сопротивление материалов
Файл:

3 семестр / Manchev_E_I_Posobie

.pdf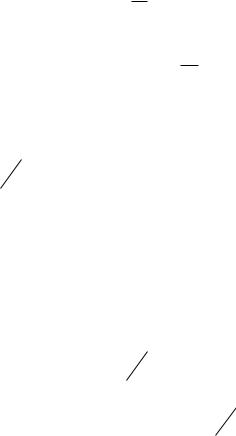
Скачиваний:
7
Добавлен:
16.05.2024
Размер:
2.41 Mб
Скачать
☆

Разделим балку на четыре силовых участка:

: 0 z1

a

: 0 z2

b

: 0 z3

c

: 0 z4

l

Рассмотрим первый силовой участок : 0 z1 a :

слева

Qy1 Fi : Ay q z1 .

i

Получили линейную зависимость

Qy1

(z1

отрезке 0 z1 a

по крайним точкам.

 

 

 

 

 

 

слева

 

 

 

 

 

M

x1

 

 

m : A

 

 

 

 

 

i

y

 

 

 

 

 

i

 

 

 

 

Получили параболическую функцию M x1

) Ay

z1 q (z1)

q z1

Строим эту функцию на

z1

 

z

.

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

z

2

 

Ay

z1

q

 

.

1

 

 

 

 

 

 

 

 

 

2

 

Для построения эпюры на этом отрезке возьмем три точки отрезка и подставим в выражение M x1 (z1 ) :

M

 

(z

0) 0;

M

 

(z

a

2

) 1.313q;

M

 

(z

a) 2.064q;

 

x1

1

 

 

x1

1

 

 

 

x1

1

 

 

 

 

 

 

 

 

 

Рассмотрим второй силовой участок

 

слева

Qy 2

 

 

i

: 0

F

: A

i

y

z

2

b

 

 

q a

:

.

Получили постоянную функцию на всем участке

 

 

 

слева

 

 

 

 

 

 

M

x2

 

 

m

: A

(z

2

a) qa

 

 

i

y

 

 

 

 

 

i

 

 

 

 

 

 

a b .

a

2

z2

 

 

 

 

 

.

Получили линейную зависимость

M

 

(z

) A

(z

 

a) qa

 

a

2

z

 

 

 

x 2

2

y

 

2

 

 

 

2

 

 

 

 

 

 

M

x 2

(z

2

0) 2.064q;

M

x 2

(z

2

b) 3.316q;

 

 

 

 

 

 

Рассмотрим третий силовой участок : 0 z3

слева

Qy3 Fi : Ay q a P Qy3 Ay q a P

i

с :

const . Получили постоянную

функцию на всем участке c.

51

 

 

 

слева

 

 

 

 

a

 

 

M

 

 

 

m

: A

(z

a b) qa

2

b

 

x3

 

 

i

y

3

 

 

 

 

 

 

 

 

 

 

 

i

 

 

 

 

 

 

 

Получили линейную зависимость:

z3

P

z3

.

M

 

(z ) A

(z

a b) qa

 

a

2

b z

 

P z

 

x3

 

3

 

 

y

3

 

 

 

 

 

3

3

 

 

 

 

 

 

 

 

 

 

 

M

x3

(z

3

0)

3.316q;

M

x3

(z

c) 0.18q;

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

Рассмотрим четвертый силовой участок :

 

 

 

справа

 

Q

y 4

 

 

F

 

 

i

 

 

 

i

 

:q

z

4

 

z

4

 

.

l

:

Получили линейную зависимость Qy 4 (z4 ) q z4

 

 

 

 

Строим эту функцию на отрезке

0 z1

l

по крайним точкам.

 

 

 

справа

 

 

 

 

 

 

 

z

 

 

 

M

 

 

 

m

: q z

 

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x4

 

 

i

 

 

 

4

 

2

 

 

 

 

 

i

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

z2

Получили параболическую функцию M

 

(z

) q

4

.

x4

 

 

 

 

 

 

 

4

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Для построения эпюры на этом отрезке возьмем три точки отрезка и подставим в выражение M x 4 (z4 ) :

M

(z 0) 0;

M

(z l

2

) 0.045q;

M

(z l) 0.18q;

x 4

4

x4

4

 

x4

4

 

 

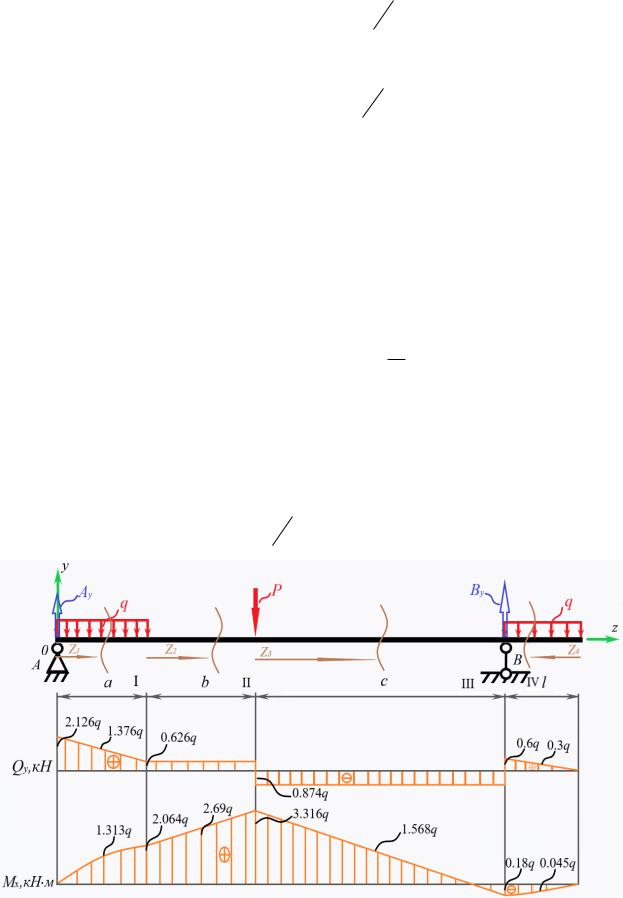
Рис.9.2 Эпюры поперечной силы и изгибающего момента

52

Из расчета на прочность определить допускаемое значение внешней нагрузки q.

Принять

P kqa,

m

qa

2

 

. Материал стержней принять из Задачи 8.

Материал стержней – сталь 10ХСНД, модуль упругости которой Е= 200 ГПа, предел текучести T 380 МПа.

Принять значение нормативного коэффициента запаса прочности

n

1.6

.

По пределу текучести и нормативному коэффициенту запаса прочности определим :

 

 

 

 

 

 

380 10

6

 

 

 

 

T

 

237.5 106

Па

 

 

 

 

 

 

 

 

 

n

 

1.6

 

 

В исходных данных дан номер профиля двутавра, который необходимо использовать для нашей конструкции – 14.

Геометрические характеристики двутавра №14:

 

 

J

 

572 см

4

;

W

81.7

см

3

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

 

Из условия прочности

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

M

max

 

 

 

3.316

q

 

 

 

 

 

 

 

 

W

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

 

q

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

W

 

 

 

W

 

 

 

 

 

 

 

 

 

 

 

3.316

 

x

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Найдем максимально допустимое значение

237.5 106 81.7 10 6 q

3.316

q :

5.852 103 Н

Для опасного сечения балки при q=[q] построить эпюру нормальных напряжений.

Опасным является сечение с координатой z a b , т.к. в этой точке эпюра изгибающего момента достигает своего максимума.

 

 

 

M

x

y

 

 

 

 

 

 

 

 

 

 

M

x

J

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

Построим эпюру нормальных напряжений. Здесь y меняет свои значения по

высоте поперечного сечения балки. У рассматриваемого двутавра №14 высота поперечного сечения h 0.14 м , следовательно на нижнем торце значение

координаты y h 2 , на верхнем – y h 2

53

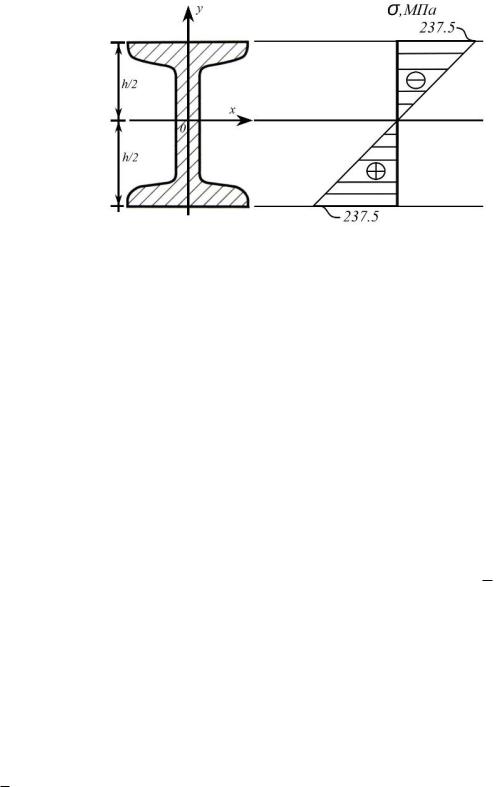
Рис.9.3 Распределение нормальных напряжений по высоте сечения двутавра

Возникает вопрос: почему в верхней части сечения балки нормальные напряжения являются отрицательными, хотя изгибающий момент в опасном сечении является положительным? Нормальные напряжения (вызываемые как раз изгибающим моментом и направленные перпендикулярно сечению) считаются положительными при растяжении и отрицательными при сжатии.

Именно знак минус в формуле для нахождения M

«исправляет» разницу в

 

x

правилах знаков для нормальных напряжений и изгибающего момента.

При внешней нагрузке, равной допускаемой, найти линейное и угловое перемещение выбранного сечения балки.

Для нахождения линейного перемещения в опасном сечении балки необходимо:

1.В выбранном сечении (z=a+b) приложить единичную силу Р=1, найти опорные реакции и построить эпюру изгибающего момента M1C

2.Вычислить интеграл Максвелла-Мора по формуле Симпсона:

Запишем интеграл Максвелла-Мора для нахождения линейных перемещений:

 

 

l

 

 

 

 

 

 

M1C M P

dz

 

 

 

CP

 

 

 

EJ

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

x

где M P – это изгибающий момент от всех внешних нагрузок т.е. эпюра M x , а

M1C – это эпюра от единичной силы

 

 

 

 

 

 

 

 

 

Такой интеграл удобно решать с помощью формулы Симпсона:

 

l

 

 

 

l

 

 

 

l

 

 

 

 

 

 

 

 

CP

 

M P (0) M1C (0)

4M P

 

 

M1C

 

 

M P l M1C l

 

 

 

 

6EJ x

2

 

 

 

2

 

 

 

 

54

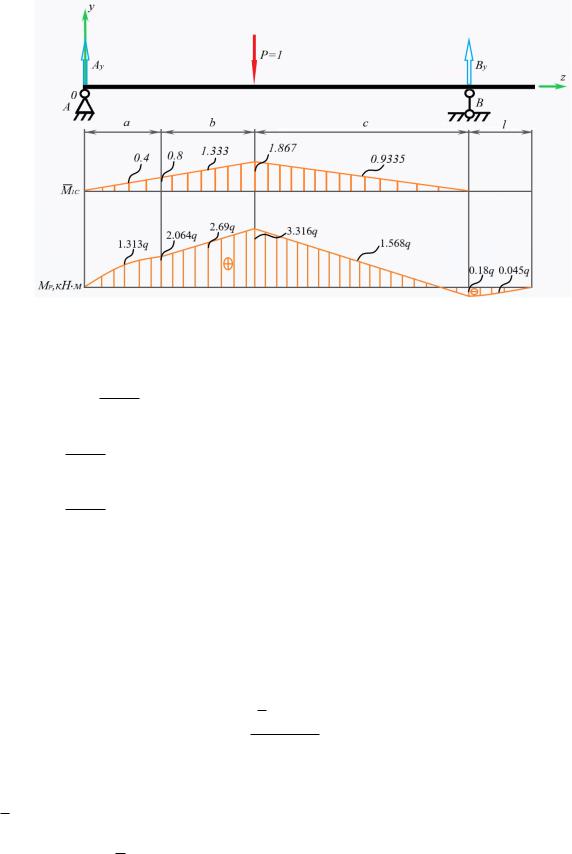
Рис.9.4 Эпюра изгибающего момента от приложенной единичной силы

 

 

 

a

 

0

0

4 1.313q 0.4 2.064q 0.8

 

 

CP

6EJ

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

b

2.064q 0.8 4 2.69q 1.333 3.316q

1.867

6EJ

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

c

3.316q 1.867 4 1.568q 0.9335 ( 0.18q) 0 0.084 м

6EJ

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Получили значение линейного перемещения балки в т. z=a+b

 

CP

 

0.084

м

.

Положительное значение CP показывает, что направление прогиба совпадает с направлением приложенной единичной силы.

Запишем интеграл Максвелла-Мора для нахождения угловых перемещений:

l

M

 

 

M

 

 

 

 

 

 

 

 

 

 

1

 

 

P

dz

 

EJ

x

 

0

 

 

 

 

 

 

 

 

где M P – это изгибающий момент от всех внешних нагрузок т.е. эпюра

M1 – это эпюра от единичного момента.

M

x

 

, а

Строим эпюру M1 . Для этого прикладываем в точке z=a+b единичный момент в направлении предполагаемого поворота сечения и находим опорные реакции

55

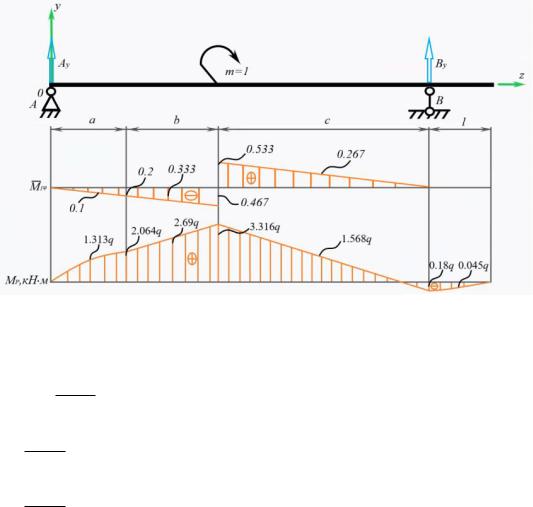
Рис.9.5 Эпюра изгибающего момента от приложенного единичного момента

 

a

0

0

4 1.313q 0.1 2.064q 0.2

 

 

6EJ

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

 

b

2.064q 0.2 4 2.69q 0.333

3.316q 0.467

 

 

6EJ

 

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

c

3.316q 0.533 4 1.568q 0.267

( 0.18q) 0 0.013 рад

6EJ

 

x

 

 

 

 

 

 

 

 

 

 

Положительное значение углового перемещения

φ 0.013

рад

показывает,

что поворот выбранного сечения происходит в направлении приложенного единичного момента.

56

ЛИТЕРАТУРА

1.Хроматов В.Е. Лекции по сопротивлению материалов в структурнологических схемах: учеб. Пособие/ В.Е. Хроматов, О.В. Новикова; под. Ред. В.П. Николаева. – 2-е изд., испр. – М.: Издательский дом МЭИ, 2020. – 220 с.

2.Москвин В.Г. Сопротивление материалов. Примеры решения задач: практикум/ В.Г. Москвин, О.В. Новикова, С.А. Монин; под. ред. В.Е. Хроматова. – М.: Издательство МЭИ, 2020 – 80 с.

3.Окопный Ю.А., Радин В.П., Хроматов В.Е., Чирков В.П. Механика материалов и конструкций. Сборник задач: Учеб. пособие для вузов/ Под ред. В.П. Чиркова. М.: Машиностроение, 2004. – 416 с.

4.Минин Л.С. Специальное конструирование. Основы специального конструирования. – М.: Издательство МЭИ, 1978. – 80 с.

57

Соседние файлы в папке 3 семестр
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности