Добавил:

Chupapi_Munyanya Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МЭИ»

Предмет:

Сопротивление материалов

Файл:

3 семестр / Manchev_E_I_Posobie

.pdf

Скачиваний:

Добавлен:

16.05.2024

Размер:

2.41 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 63 4 5 6 > Следующая >>>

Часть II. Напряженно-деформированное состояние в точке. Тензор напряжений

Задача 5

1.Получить характеристическое уравнение для определения главных

значений (главных напряжений) и системы уравнений для нахождения направлений главных осей тензора напряжений .

2.Для проверки правильности найденных корней характеристического уравнения, вычислить инварианты тензора напряжений в исходных и главных осях.

3.Вычислить главные значения и направляющие косинусы главных осей

jk , МПа

4. По заданному критерию прочности вычислить эквивалентные напряжения.

Исходные данные

	11	МПа	22	МПа	33	МПа		12	=	21	МПа	12	=	21	МПа	23	=	32	МПа
	11		22		33			12		21		12		21		23		32
	-70		-20		50				-10				-10				22
Критерий прочности – Мизеса
Запишем тензор в матричной форме:
					70		10		10
						10	20		22										(5.1)
						10	20		22										(5.1)
						10	22		50
						10	22		50

NB! Главные напряжения – это нормальные напряжения, действующие по площадкам, где отсутствуют касательные напряжения. Координатные оси,

являющиеся нормалями к таким площадкам, называются главными осями тензора напряжений, а сами площадки – главными площадками.

Главные значения (главные напряжения) определяются из уравнения

	3	I1	2	I	2 I3 0	(5.2)
	3		2

где I1, I2 , I3 это инварианты напряженного состояния (самого тензора).

NB! Инвариант – это величина, которая не зависит от системы координат.

Выражения для нахождения инвариантов:

(5.3)

Условием существования собственных значений матрицы является равенство нулю определителя, составленного из этой матрицы (в нашем случае из матрицы (5.1)), в которой к диагональным элементам прибавляем .

Получится:

70	10	10
10	20	22	0
10	22	50

(5.4)

Раскрывая этот определитель, получим характеристическое уравнение для нахождения собственных значений матрицы (5.1)

	3	( 40)		2	( 3784) 105280 0
	3			2

Сравнивая (5.5) и (5.2), нетрудно догадаться, что

I1 40 I2 3784 I3 105280

Попробуем теперь найти инварианты по формулам (5.3)

I	1	70 20 50 40
	1
I		70 ( 20) ( 20) (50) (50) ( 70) ( 10)				2	(22)	2	( 10)	2	3784
I	2	70 ( 20) ( 20) (50) (50) ( 70) ( 10)					(22)		( 10)		3784
	2
		70	10	10
I	3	10	20	22	105280
	3
		10	22	50

(5.5)

Получается то же самое, следовательно, использование формул (5.3) позволяет проверить правильность получения характеристического уравнения (5.5), получаемого при раскрытии определителя (5.4).

Решим это характеристическое уравнение (5.5):

(Можно пользоваться программными комплексами, можно решить аналитически с помощью метода Кардано)

Выберем первый вариант. Кубическое уравнение (5.5) имеет 3 корня:

57.547; –72.212; –25.335

Индексация этих трех корней проводится по такому правилу:

			1			max	3	min
			1			max	3	min
Значит:
	1	57.547		2	25.335				3	72.212
	1			2					3

Известно, что на главных площадках отсутствуют касательные напряжения, поэтому тензор в главных осях будет иметь такой вид:

57.547	0	0
0	25.335	0
0	25.335	0

0	0	72.212
0	0	72.212

(5.6)

Выполним проверку правильности найденных главных напряжений. Для этого необходимо найти инварианты тензора (5.6).

Они					должны								совпадать с					найденными ранее значениями
I	1		1				2			3		40
I	1		1				2			3						(0)		(0)		(0)		3784
I																(0)	2	(0)	2	(0)	2	3784
																	2		2		2
	2		1			2			1				3	2	3
				1		0			0
				1
I	3	0						2	0			105280
	3							2
		0				0					3
											3

I	1	,
	1

I	2	, I	3

Совпадают.

Каждому

значению

	j

( j

1,2,3)

соответствует

вектор

n	j

направляющих

косинусов, определяющих направление главных площадок по отношению к исходной системе координат:

cos(x, x

); n

cos( y, y

); n

cos(z, z

Компоненты этого вектора направляющих косинусов определяются из системы алгебраических уравнений:

(

) n

( y

j ) ny

ny ( z

j ) nz

которые должны быть дополнены условием нормировки:

где j 1,2,3.

(5.7)

(5.8)

NB!

n	j	, n	j
	x		y

Определитель, составленный из коэффициентов при неизвестных

j	системы уравнений (5.7), равен нулю.
, nz

Следовательно, три уравнения в (5.7) являются линейно зависимые: одно уравнение (любое) является следствием двух других. Поэтому для определения направляющих косинусов nxj , nyj , nzj любой главной оси нужно

любое из уравнений удалить и к двум оставшимся добавить уравнение (5.8).

Решив полученную систему трех уравнений с тремя неизвестными, найдем

j	j	j	, соответствующие главному напряжению
направляющие косинусы nx	, ny	, nz	, соответствующие главному напряжению

. Положение оставшихся двух осей находят аналогично.

	j

Нужно иметь в виду, что каждый из направляющих косинусов получается с двумя знаками. Знаки соответствуют повороту осей по часовой стрелке или против часовой стрелки. При этом главные оси занимают одно и то же положение, но направлены в противоположные стороны. При определении положения главных осей нужно оставить одну систему знаков, конкретизировав при этом направления осей.

Например:

1	1	1	составим такую систему уравнений:
Для nx	, ny	, nz	составим такую систему уравнений:

( x 1 ) n1x xy n1y xz n1zyx n1x ( y 1 ) n1y yz n1z

n1x 2 n1y 2 n1z 2 1

Поделим два первых уравнения на n1 и получим z

						n			n
( x	1 )					1		xy		1		xz
( x	1 )						1	xy			1	xz
							x				y
						nz			nz
			1								1
yx		n			( y			1 )	n		1
yx			1		( y			1 )			1	yz
				x							y
nx		nz			ny			nz	nz
nx					ny			nz		1
1		2			1		2	1	2

Подставим найденные ранее значения нормальных, касательных и главных напряжений в эту систему и получим:

				n			n
				1				1
( 70 57.547)					x	10		y		10
( 70 57.547)				1		10		1		10
				nz			nz
	1								1
10	n	x	( 20 57.547)					n		y
		x								y	22
	1									1	22
	nz							nz

nx		ny		nz		1
1	2	1	2	1	2

Предоставим программному комплексу Mathcad 15 решить эту систему:

	1		0.097		0.097
n		x

	1			0.283	0.283
	n	y

	1			0.954	0.954
n		z

Возьмем значения из 1-го столбца и найдем значения углов. Углы, которые составляет первая главная ось тензора напряжений с исходными осями координат, находятся вычислением функции arccos от n1x , n1y , n1z :

(x,	0	'	; ( y,	0	'	)
(x,	) 95 57		; ( y,	) 73 55 ; (z,		)
1			1		1

17	0	42	'

Аналогично для nx2 , ny2 , nz2

(

) n2

(

) n2

nx2 2 ny2 2 nz2 2 1

0 и т.д.

Получим:

n		2	0.145	0.145
		x

	n	2	0.944	0.944
		y

n		2	0.295	0.295
		z

(x,		0	'	; ( y,		) 160	0	79	'	; (z,		0	'
(x,	2	) 81 64		; ( y,	2	) 160		79		; (z,	2	) 72 84
	2				2						2

			3		3	3
И для nx				, ny		, nz
Получим:
n		3				0.984
		x

	n	3				0.167
		y

		3				0.050
nz

	0.984
	0.167


	0.050

(x,		) 10	0	07	'	; ( y,	) 80	0	37	'	; (z,	0 '
(x,	3	) 10		07		; ( y,	) 80		37		; (z,	) 87 11
	3					3					3

Как проверить правильность найденных nxj , nyj , nzj ?

Проверка правильности вычисления положения главных осей тензора напряжений основана на свойствах матрицы направляющих косинусов. Она относится к ортогональным матрицам и обладает следующими свойствами:

–Определитель ортогональной матрицы равен единице.

–Сумма квадратов элементов, входящих в каждую строку (столбец) равна единице.

–Если рассматривать каждую строку матрицы как вектор-строку, а каждый столбец – как вектор-столбец, то скалярные произведения двух разных векторов-строк (векторов-столбцов) равны нулю.

Воспользуемся первым свойством ортогональных матриц.

Составим определитель из

n	j	, n	j	, n	j
	x		y		z

и проверим, равен ли он единице:

1		1			1	0.097	0.283	0.954
n	x	n	y	n	z

n	2	n	2	n	2	0.145	0.944	0.295 0.9999999986869448238139 1
	x		y		z

n	3	n	3	n	3	0.984	0.167	0.050
	x		y		z

Даже с учетом всех округлений получилось очень близкое к 1 число.

По заданному критерию прочности Мизеса вычислим эквивалентные напряжения:

экв 1 2 2 2 3 2 1 2 1 3 2 3 113.807 МПа

Часть III. Определение усилий в элементах статически неопределимых конструкций

Пример. 3 Решение статически неопределимой задачи с помощью составления уравнения совместности деформаций

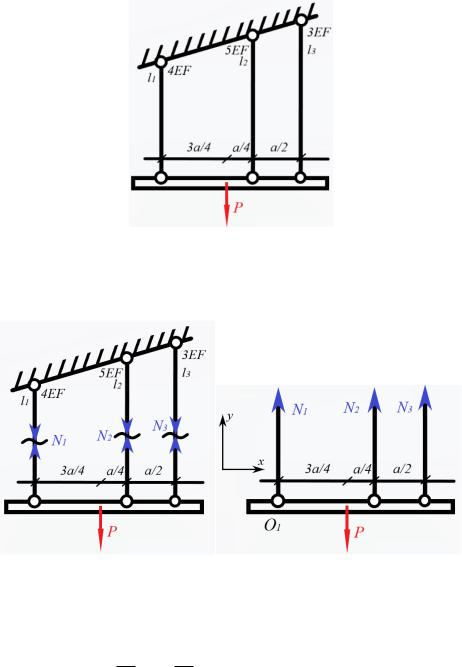
Абсолютно жесткий брус закреплен на трех стрежнях и нагружен силой Р. Определить неизвестные усилия в стержнях.

l1 3м; l2 4м; l3 4.5м; F 2 10 4 м2 ; 160 МПа; E 200 10 9 Па

Допустим, что во всех стержнях системы возникают растягивающие усилия. Укажем их на исходной системе, воспользовавшись методом сечений, и рассмотрим равновесие отсеченной нижней части.

Составим три уравнения статики для плоской системы:

X 0

Y 0 : N1 N2 N3 P 0

momO1 0 : N2 a N3 32a P 34a 0

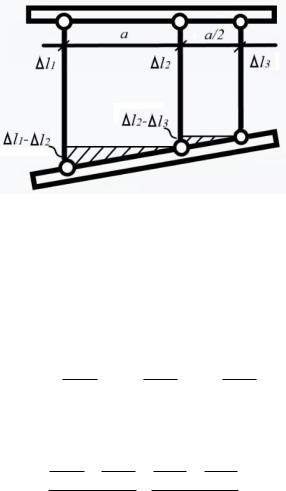
Имеем два нетривиальных уравнения статики и три неизвестных усилия. Система 1 раз статически неопределима. Дополним уравнения статики одним уравнением совместности деформаций. Допустим, что брус под действием силы сместится вниз. Отметим отрезки удлинений стержней l1, l2 , l3

Установим геометрическую связь между деформациями стержней.

Проведем горизонтальные линии в трапеции деформаций и запишем уравнения подобия прямоугольных треугольников:

		l	l	2			l	l
		1		2	=		2	3
			а		=		а / 2
			а				а / 2
Деформации стержней:
		N l				N l				N l
l	=	1 1	, l	=			2 2	, l	=	3 3
1		4EF	2			5EF		3		3EF
		4EF				5EF				3EF

Подставим в уравнение совместности деформаций:

N l		N l		N l		N l
1 1		2 2		2 2		3 3

4EF		5EF	=	5EF		3EF
	а				а / 2

Объединим уравнения статики и совместности деформаций:

N1 N2 N3 P 0
N2 N3		3	P				3	0
N2 N3		2	P				4	0
		2					4
3N l	4N			l	2				4N	l	2	4.5N l
1 1		2			2	=2			2		2	3 3
4		5				=2			5			3
4		5							5			3

Решая эту систему, получим значения неизвестных усилий:

N1 =0.366P, N2 =0.4P, N3 0.231P

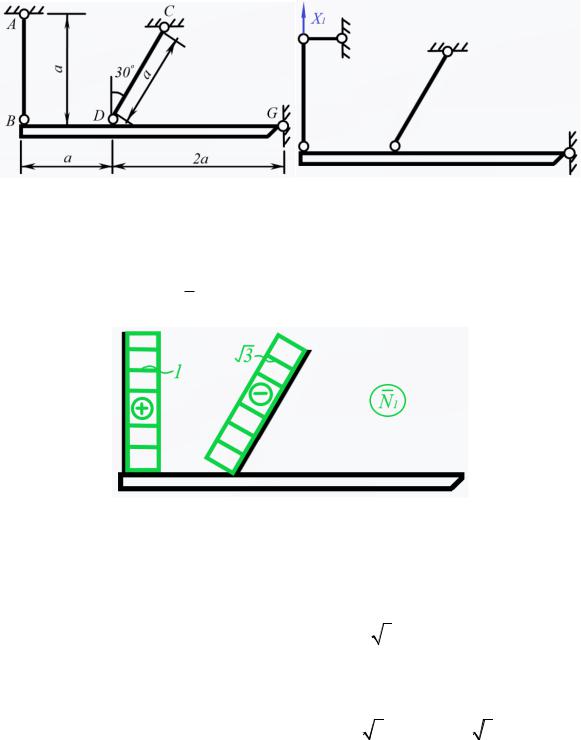
Пример 4. Применение метода сил для систем, работающих на растяжение-сжатие

Определим усилия, возникающие при нагреве обоих стержней на T считаем абсолютно жестким. Система имеет одну лишнюю связь. основную систему.

Вид канонического уравнения:

	11	X	1		0
	11		1	1T

. Брус BG Начертим

Приложим к основной системе единичную силу

эпюру продольной силы

N1 .

X	1

и построим единичную

Для нахождения единичного перемещения 11 воспользуемся формулой:

N j

i 1

i 2

4 a

N j

i 1

Для вычисления температурного перемещения воспользуемся формулой:

i 2
		i Ta 1 Ta	3 Ta	3 1
jT TlN	1
i 1

Подставляя найденные коэффициенты в каноническое уравнение, определим лишнюю неизвестную:

X			0.18 TEF
X		1T	0.18 TEF
		1T
	1

		11

Усилие во втором стержне можно найти, умножив на единичной продольной силы во втором стержне N1

получим:

X1 значение эпюры от3 . В результате,

С 0.32 TEF

<<< < Предыдущая 1 23 / 63 4 5 6 > Следующая >>>

Соседние файлы в папке 3 семестр

#
16.05.20242.41 Mб1Manchev_E_I_Posobie.pdf
#
16.05.2024687.86 Кб0Данные к задачам для расчеток.pdf
#
16.05.20244.24 Mб0Долгов Р ТФ-14-20 РЗ.pdf
#
16.05.20241.12 Mб0Задачи для расчеток.pdf
#
16.05.202416.87 Кб0Темы лекций и практик.docx

						n			n
( x	1 )					1		xy		1		xz
( x	1 )						1	xy			1	xz
							x				y
						nz			nz
			1								1
yx		n			( y			1 )	n		1
yx			1		( y			1 )			1	yz
				x							y
nx		nz			ny			nz	nz
nx					ny			nz		1
1		2			1		2	1	2

						n			n
( x	1 )					1		xy		1		xz
( x	1 )						1	xy			1	xz
							x				y
						nz			nz
			1								1
yx		n			( y			1 )	n		1
yx			1		( y			1 )			1	yz
				x							y
nx		nz			ny			nz	nz
nx					ny			nz		1
1		2			1		2	1	2

						n			n
( x	1 )					1		xy		1		xz
( x	1 )						1	xy			1	xz
							x				y
						nz			nz
			1								1
yx		n			( y			1 )	n		1
yx			1		( y			1 )			1	yz
				x							y
nx		nz			ny			nz	nz
nx					ny			nz		1
1		2			1		2	1	2