
3 семестр / Manchev_E_I_Posobie
.pdfРЕШЕНИЕ ТИПОВЫХ ЗАДАЧ ПО СОПРОТИВЛЕНИЮ МАТЕРИАЛОВ
В пособии приведены подробные решения задач по расчету на прочность при растяжении-сжатии и изгибе статически определимых и статически неопределимых систем, а также решение задачи на определение главных напряжений.
СОДЕРЖАНИЕ Предисловие……………………………………………………………3
Часть I. Определение усилий в элементах статически определимых конструкций……………………………………………………………4
Примеры расчета простых стержневых конструкций на растяжение-
сжатие…..................……………………………………………………4
Задача 1…………………………………………………………………9 Задача 2………………………………………………………………..12 Задача 3………………………………………………………………..15 Задача 4………………………………………………………………..17
Часть II. Напряженно-деформированное состояние в точке. Тензор напряжений………………………………………………..…………..21
Задача 5………………………………………………………………..21
Часть III. Определение усилий в элементах статически неопредели-
мых конструкций……………………………………………………..27
Примеры решения статически неопределимой задач……………...27
Задача 6………………………………………………………………..31 Задача 7………………………………………………………………..37
Часть IV. Расчет на прочность статически определимых балок…..38
Задача 8………………………………………………………………..42 Задача 9………………………………………………………………..50
2
ПРЕДИСЛОВИЕ
Данная работа является первой попыткой магистра 6 курса НИУ «МЭИ» кафедры Робототехники и мехатроники, динамики и прочности машин составить пособие, которое могло бы подготовить студента к выполнению типового расчета по дисциплине «Сопротивление материалов». Успешные сдачи контрольных работ, курсовых проектов в значительной степени зависят от количества рассматриваемых на семинарах задач. Подобно космонавту, который изучает максимум нештатных ситуаций, чтобы быть готовым справиться с любым неожиданным происшествием на орбите, студент должен получить примеры большинства задач, которые могут попасться на контрольной работе, в курсовом проекте, на экзамене, чтобы правильно решить и нерассмотренную доселе задачу. Подобная практика исстари считается самой эффективной. Только изучив достаточное количество примеров, в которых даются самые подробные объяснения, можно научиться созиданию – составлению и решению собственных задач. Понимание дисциплины приходит со временем. Здесь уместно вспомнить выражение «коридорный ответ»: если студент способен в перерыве объяснить своему товарищу на простых примерах какую-нибудь тему, то понимание есть. Данная работа – это пример выполнения курсового проекта, а наряду с усвоенным теоретическим материалом правильно выполненный курсовой проект – гарантия получения хорошей отметки на экзамене. Любой расчет или объяснение теоретического материала должны сопровождаться примерами из жизни и вопросами для самоконтроля. В таком случае, у студента никогда не возникнет вопроса: «А где такое может встретиться в жизни, на работе?». Великий советский конструктор Юлий Борисович Харитон любил повторять: «Знать надо в десять раз больше того, что мы делаем». Любым знаниям можно найти применение.
3
Часть I. Определение усилий в элементах статически определимых конструкций
Пример 1
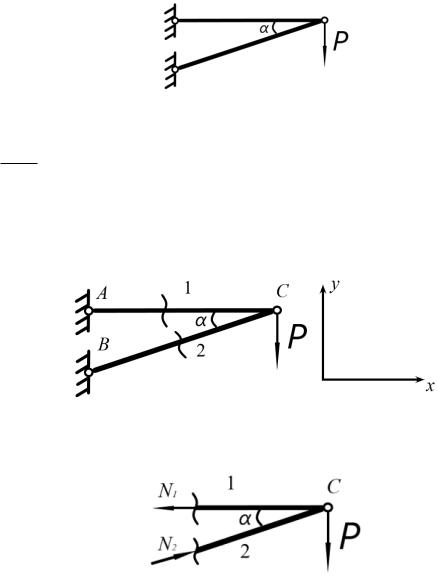
Рассмотрим кронштейн, нагруженный вертикальной силой Р=100 кН. Пусть угол α=30 , а площадь поперечного сечения стержней F1=F2=F. По допускаемым напряжениям [σ]=120 МПа определить минимальную площадь поперечного сечения, при которой будет выполняться условие прочностиmax . (Формой сечения выбрать двутавр)
Для нахождения максимальных напряжений, определяемых по формуле
max |
|
|
N |
max |
|
|
F |
|
, найдем усилия, которые возникают в стержнях, т.е.
N |
, N |
2 |
1 |
|
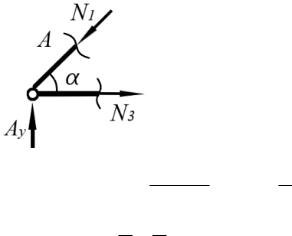
1) Будем рассматривать схему нагружения в рамках декартовой СК. Пронумеруем стержни; буквами А и В обозначены точки закрепления, буквой С обозначена точка соединения двух стержней – узел.
2) Для определения внутренних усилий |
N1, N2 |
воспользуемся методом |
вырезания узлов. Рассмотрим узел С. |
|
|
Направление усилий N1, N2 выбираем произвольно.
Для выбора направлений N1, N2 можем предположить, что:
– усилие N1 будет компенсировать растягивающее воздействие силы Р на стержень 1
4
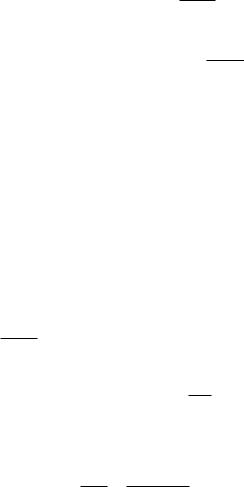
– усилие N2 будет компенсировать сжимающее воздействие силы Р на стержень 2
Получаем систему трех сходящихся сил |
|
N1, N2 , Р . |
|
|||||||||||
3) Для нахождения неизвестных сил |
|
|
в узле С N1, N2 нужно |
составить 2 |
||||||||||
уравнения статики (сумма проекций всех сил на ось X и Y) |
|
|||||||||||||
|
|
|
|
|
|
|
|
X 0 |
|
|||||
|
|
|
|
|
|
|
|
Y 0 |
|
|
||||
X 0 : |
N N |
2 |
cos α 0 N N |
2 |
|
cosα |
(1) |
|||||||
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
||
Y 0 : |
N |
|
sin α P 0 N |
|
|
P |
|
|
|
|
|
(2) |
||
2 |
2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
sin α |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Подставляя |
(2) (1) , получим |
N1 |
|
P |
|
cos |
|
|||||||
sin |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
Зная значение угла α и силы Р, получим численное значение усилий
N |
, N |
2 |
1 |
|
:
N |
|
1 |
|
N |
2 |
|
|
Положительные значения усилий изначально направления оказались
173,2 кН
200 кН
N1, N2 показывают, что предположенные правильными.
4) Подберем поперечное условия прочности max
сечение для |
|
|
|
|
|
наших стержней для удовлетворения
Т.к. max NFmax , то условие прочности в нашем случае будет иметь вид:
N |
2 |
|
|
|
|
|
|
F |
|
|
|
Из условия прочности находим минимальное допускаемое значение F
FN2 200 103 0,001667 м2 16,67 см2
120 106
В таблице двутавровых профилей ближайшим к такой площади поперечного сечения является двутавр №14 c F 17.4 см2
5) Выполним прочностную проверку:
|
|
|
|
|
max |
|
|
|
|
|
5
Nmax N2
max |
F |
F |
|
выполняется
|
3 |
|
|
|
|
|
|
200 10 |
114,9 10 |
6 |
120 10 |
6 |
– условие прочности |
|
||||||
0.00174 |
|
|
||||
|
|
|
|
|
|
Пример 2
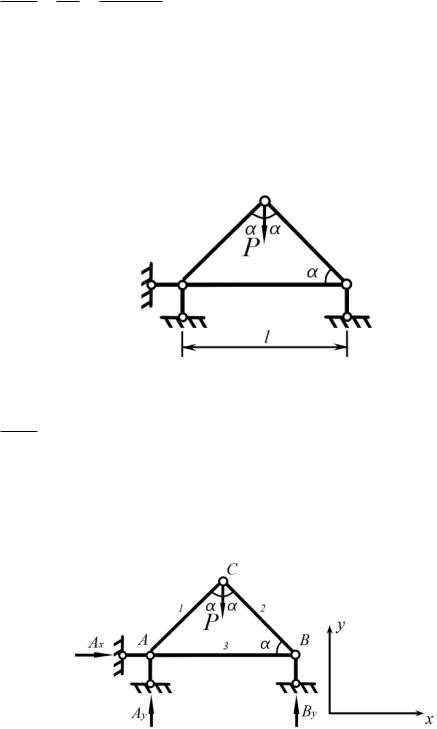
Рассмотрим ферму, нагруженную вертикальной силой Р=65 кН. Пусть угол α=45 , а площадь поперечного сечения стержней F1=F2= F3=0,000405 м2. По допускаемым напряжениям [σ]=120МПа проверить выполняется ли условие прочности max .
Для нахождения максимальных напряжений, определяемых по формуле
max |
|
|
N |
max |
|
|
F |
|
, найдем усилия, которые возникают в стержнях, т.е.
N |
, N |
, N |
3 |
1 |
2 |
|
1) Будем рассматривать схему нагружения в рамках декартовой СК. Пронумеруем стержни; буквами А и В обозначены шарнирно-неподвижная и шарнирно-подвижная опоры, буквой С обозначена точка соединения стержней 1 и 2 – узел.
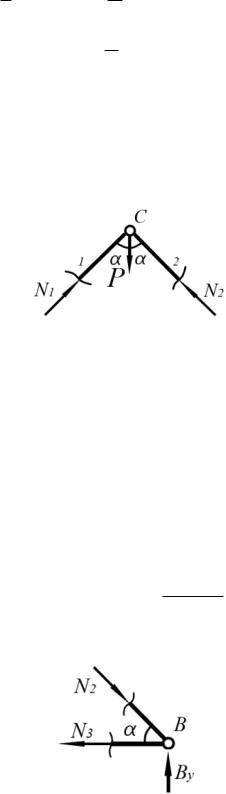
2) Вначале определяем опорные реакции. Составляем уравнения статики (сумма моментов всех сил относительно точки А и сумма проекций всех сил на ось Y):
6
momA 0 : B |
|
l P |
l |
0 B |
|
|
P |
(2.1) |
|
y |
2 |
y |
2 |
||||||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||
Y 0 : A B |
|
P 0 |
A |
|
|
P |
(2.2) |
||
y |
|
|
|||||||
y |
|
|
y |
|
2 |
|
|||
|
|
|
|
|
|
|
|
||
(При составлении суммы проекций всех сил равной нулю)
3) Для определения внутренних усилий |
N1, |
вырезания узлов. Рассмотрим узел С. |
|
на
N |
, |
2 |
|
ось Х реакция Ax
N3 воспользуемся
окажется
методом
Направление усилий
N |
, N |
2 |
1 |
|
выбираем произвольно предполагая, что
N |
, N |
2 |
1 |
|
будут компенсировать сжимающее воздействие силы Р на стержни 1 и 2.
Получаем систему трех сходящихся сил |
N1 |
, N2 , Р . |
|
|||||
Составляем 2 уравнения статики (сумма проекций всех сил на ось X и Y) |
|
|||||||
|
|
|
|
X 0 |
|
|
||
|
|
|
|
Y 0 |
|
|
||
X 0 : N |
sin N |
2 |
sin 0 N N |
2 |
|
(2.3) |
||
1 |
|
|
1 |
|
|
|
||
Y 0 : N cos N |
|
|
cos P 0 N |
P |
(2.4) |
|||
2 |
|
|||||||
1 |
|
1 |
|
|
2 cos |
|
||
|
|
|
|
|
|
|
|
|
Рассмотрим точку В
Для выбора направления усилия N2 следуем принципу соответствия, который
гласит, что в рамках одного стрежня, ограниченного двумя узлами, внутреннее усилие должно иметь одинаковый характер воздействия на оба узла; в данном случае – сжимающий (сжимает узлы С и В). Предположим, что усилие N3
7
оказывает растягивающее воздействие на узел В. Значение реакции опоры
B |
y |
|
и
усилия N2 уже известны, |
поэтому |
||
статики для нахождения N3 |
: |
|
|
X 0 : N2 cos N3 0 N3 |
P |
||
2 |
|||
|
|
||
достаточно составить одно уравнение
(2.5)
Все внутренние усилия найдены. Узел А можно рассмотреть в качестве проверки:
X 0 : N |
cos N |
|
0 N cos N |
|
|
|
|
P |
|
cos |
P |
(2.6) |
|
3 |
3 |
|
|
|
|
|
|||||||
1 |
|
|
1 |
|
|
2 cos |
|
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
||||
Y 0 : A N sin 0 A |
N sin |
P |
|
P |
tg 45 |
o |
|
|
(2.7) |
||||
|
|
|
|
||||||||||
|
|
|
|
|
|||||||||
y |
1 |
|
y |
1 |
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Зная значение угла α и силы Р, получим численные значения усилий N1, N2 , N3 |
|||||||||||||
|
|
|
|
N1 45,96 кН |
|
|
|
|
|
|
|
||
|
|
|
|
N2 45,96 кН |
|
|
|
|
|
|
|
||
|
|
|
|
N3 32,5 кН |
|
|
|
|
|
|
|
|
|
Положительные значения усилий N1, N2 , N3 |
показывают, что предположенные |
||||||||||||
изначально направления оказались правильными.
4) Проверим условие прочности
|
|
|
|
|
max |
|
|
||
|
|
|
|
|
|
|
Nmax |
|
45,96 103 |
113,5 106 120 106 |
max |
|
|
||||
|
|
F |
0,000405 |
|
||
|
|
|
|
|||
Условие прочности выполняется.
8
Задача 1
1.Провести анализ системы с точки зрения ее статической определимости.
2.Определить реакции связей системы и усилия в стержнях (тросах) при ее квазистатическом нагружении внешними силами.
3.Выполнить проверку полученного решения. Погрешность не должна превышать 3%.
4.Из условия прочности тросов найти их диаметры. Принять =160 МПа.
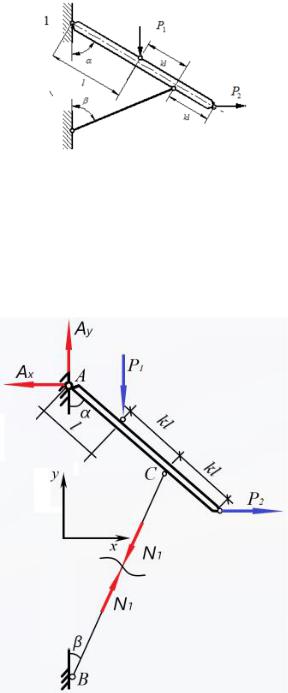
Рис.1.1 Схема нагружения
Исходные данные:
P1 |
кН |
P2 |
кН |
m |
кН |
м |
α |
o |
β |
o |
l |
м |
k |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
3 |
|
4 |
|
1.3 |
|
45 |
20 |
|
3 |
1.2 |
||
Рис.1.2 Схема нагружения с соблюдением масштабов
9
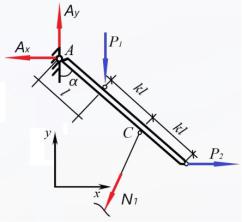
Будем рассматривать схему нагружения в рамках декартовой СК. Буквами А и В обозначены точки закрепления, буквой С обозначена точка соединения стержня 1 (троса) и абсолютно жесткого стержня.
Вточке А – жесткая заделка, ограничивающая вертикальные и горизонтальные перемещения абс. жетского стержня. Значит, в ней булут возникать две реакции.
Вточке В – тоже жесткая заделка, но так как к ней шарнирно присоединен стержень (трос), работающий только на растяжение, то реакцию в ней можно не рассматривать.
1. Провести анализ системы с точки зрения ее статической определимости.
В точки зрения статической определимости, схема нагружения является статически определимой: для находжения 3 неизвестных (реакций Ах, Ау и усилия N1) можно составить 3 уравнения статики.
2. Определить реакции связей системы и усилия в стержнях (тросах) при ее квазистатическом нагружении внешними силами.
Рис.1.3 Неизвестные реакции и усилие
X 0 : P2 Ax N1 sin |
0 |
|
|||||||||
Y 0 : Ay P N cos 0 |
|
||||||||||
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
momA 0 : |
|
P |
|
|
sin l |
|
N |
||||
2 |
|
|
|
|
|
|
|
|
|
|
|
P |
|
l 2 kl |
|
cos |
|
0 |
|
|
|
||
NB |
sin l , l kl |
|
cos , |
l |
|||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
sin |
l |
kl sin |
|
|
|
|
|
|
1 |
|
|
|
|
|
kl |
|
cos |
N |
cos |
l kl |
|
sin |
|
, l 2 kl cos – плечи.
Так как усилие N1 постоянно по всей длине стержня BC, то для нахождения его момента относительно т.А мы можем выбрать точкой приложения любую точку на стержне ВС. Удобно выбрать либо B, либо С. Выберем т.С
10
