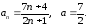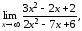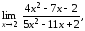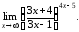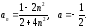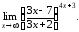- •Типовой расчет «пределы» Вариант 1
- •Типовой расчет «пределы»
- •Типовой расчет «пределы» Вариант 3
- •Типовой расчет «пределы» Вариант 4
- •Типовой расчет «пределы» Вариант 5
- •Типовой расчет «пределы» Вариант 6
- •Типовой расчет «пределы» Вариант 7
- •Типовой расчет «пределы» Вариант 8
- •Типовой расчет «пределы» Вариант 9
- •Типовой расчет «пределы» Вариант 10
- •Типовой расчет «пределы» Вариант 11
- •Типовой расчет «пределы» Вариант 12
- •Типовой расчет «пределы» Вариант 13
- •Типовой расчет «пределы» Вариант 14
- •Типовой расчет «пределы» Вариант 15
- •Типовой расчет «пределы» Вариант 16
- •Типовой расчет «пределы» Вариант 17
- •Типовой расчет «пределы» Вариант 18
- •Типовой расчет «пределы» Вариант 19
- •Типовой расчет «пределы» Вариант 20
- •Типовой расчет «пределы» Вариант 21
- •Типовой расчет «пределы» Вариант 22
- •Типовой расчет «пределы» Вариант 23
- •Типовой расчет «пределы» Вариант 24
- •Типовой расчет «пределы» Вариант 25
Типовой расчет «пределы» Вариант 1
1.
Доказать,
что
 (указать
(указать
 ).
).
|
а)
|
б)
|
|
|
|
|
|
2. Вычислить пределы:
|
а)
|
б)
|
в)
|
|
г)
|
д)
|
е)
|
3. Заданы функция y = f(x) и два значения аргумента x1 и x2. Требуется:
1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента; 2) в случае разрыва функции найти ее пределы в точке разрыва слева и справа; 3) сделать схематичный чертеж.
f(x)= ,
x1
=
6, x2
=
– 4.
,
x1
=
6, x2
=
– 4.
4. Задана функция y = f(x). Найти точки разрыва функции, если они существуют. Сделать чертеж.

Типовой расчет «пределы»
Вариант 2
1.
Доказать,
что
 (указать
(указать
 ).
).
|
а)
|
б)
|
|
2. Вычислить пределы:
|
а)
|
б)
|
в)
|
|
г)
|
д)
|
е)
|
3. Заданы функция y = f(x) и два значения аргумента x1 и x2. Требуется:
1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента; 2) в случае разрыва функции найти ее пределы в точке разрыва слева и справа; 3) сделать схематичный чертеж.
f(x)= ,
x1
=
–3, x2
=
0.
,
x1
=
–3, x2
=
0.
4. Задана функция y = f(x). Найти точки разрыва функции, если они существуют. Сделать чертеж.

Типовой расчет «пределы» Вариант 3
1.
Доказать,
что
 (указать
(указать
 ).
).
|
а)
|
б)
|
|
2. Вычислить пределы:
|
а)
|
б)
|
в)
| ||
|
г)
|
д)
|
е)
| ||
3. Заданы функция y = f(x) и два значения аргумента x1 и x2. Требуется:
1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента; 2) в случае разрыва функции найти ее пределы в точке разрыва слева и справа; 3) сделать схематичный чертеж.
f(x)= ,
x1
=
4, x2
=
0.
,
x1
=
4, x2
=
0.
4. Задана функция y = f(x). Найти точки разрыва функции, если они существуют. Сделать чертеж.

Типовой расчет «пределы» Вариант 4
1.
Доказать,
что
 (указать
(указать
 ).
).
|
а)
|
б)
|
|
2. Вычислить пределы:
|
а)
|
б)
|
в)
| ||
|
г)
|
д) |
е)
| ||
3. Заданы функция y = f(x) и два значения аргумента x1 и x2. Требуется:
1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента; 2) в случае разрыва функции найти ее пределы в точке разрыва слева и справа; 3) сделать схематичный чертеж.
f(x)= ,
x1
=
0, x2
=
2.
,
x1
=
0, x2
=
2.
4. Задана функция y = f(x). Найти точки разрыва функции, если они существуют. Сделать чертеж.

Типовой расчет «пределы» Вариант 5
1.
Доказать,
что
 (указать
(указать
 ).
).
|
a)
|
б)
|
|
2. Вычислить пределы:
|
а)
|
б)
|
в)
|
|
г)
|
д)
|
е)
|
3. Заданы функция y = f(x) и два значения аргумента x1 и x2. Требуется:
1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента; 2) в случае разрыва функции найти ее пределы в точке разрыва слева и справа; 3) сделать схематичный чертеж.
f(x)= ,
x1
=
1, x2
=
3.
,
x1
=
1, x2
=
3.
4. Задана функция y = f(x). Найти точки разрыва функции, если они существуют. Сделать чертеж.