2. Современная методология оптимизации развития производств ятэк

В состав ядерного топливно-энергетического комплекса (ЯТЭК) входят следующие производства: добыча урана, изготовление топливных элементов, сжигание топлива в ядерных энергетических реакторах, химическая переработка топлива и другие.

Оптимизировать ЯТЭК - значит найти оптимальный план (решение) развития всех производств, исходя из интересов народного хозяйства. Этот план должен быть согласован по всем производствам и соответствовать минимальному значению целевой функции (функционала). Специфика этой задачи оптимизации состоит в том, что она является динамической и, как правило, с нелинейным (вогнутым) функционалом.

В настоящее время не существует общих методов решения таких сложных задач оптимизации. Решение каждой такой задачи - большое искусство.

К решению динамических плановых задач, ввязанных с развитием и размещением производства, большинство авторов подходит на основе опыта решения задач математического программирования, т.е. динамическая задача с самого начала рассматривается как серия статических задач, решаемых методами линейного или нелинейного программирования (см. §1.8). В этом случае размерность задачи (число оптимизируемых параметров) растет пропорционально числу расчетных узлов на оси времени t, что приводит к существенным трудностям при практической реализации методов. Поэтому, применяя методы линейного и нелинейного программирования, как правило, ограничивают число расчетных интервалов на оси времени t. Так, при решении задач перспективного планирования нередко переходят от годовых к пятилетним квантам времени. Естественно, точность решения при этом снижается.

Следует подчеркнуть, что получаемые задачи математического программирования не всегда являются выпуклыми. Тогда, как большинство методов математического программирования (как это показано в последующих разделах) надежно работают лишь для выпуклых задач.

Принципиально иной подход к решению динамических задач был предложен Я.В.Шевелевым [3]. Задача с самого начала рассматривается как динамическая. Время остается непрерывной переменной вплоть до того момента, пока задача не окажется сведенной к той или иной задаче анализа: например, к задаче отыскания корня функции от t или экстремума функции от t и т.п.; она может также сводиться к задаче линейного программирования, размерность которой сравнима по порядку с числом расчетных интервалов (расчетных узлов) на оси t. В свою очередь число расчетных интервалов, вводимых на заключительном этапе решения задачи динамической оптимизации, не сказывается катастрофически на трудоемкости расчета. Такие методы динамической оптимизации называют методами оптимального управления. Они позволяют отыскивать моменты проведения того или иного мероприятия, например, пуска в эксплуатацию нового завода, с точностью, определяемой полнотой и достоверностью технико-экономической информации.

Методы оптимального управления позволяют определить цены на продукцию каждого вида (как отношение увеличения затрат к соответствующему увеличению выпуска определенной продукции). Эти цены используются для отыскания структуры оптимального плана развития каждого звена (производства) ЯТЭК, а также для увязывания планов разных звеньев, т.е. для согласования планов этих звеньев, и получения оптимального согласованного плана всей системы.

Рассмотрим возможный порядок согласования планов двух звеньев ЯТЭК; звена (l-1) - поставщика продукции и звена l - потребителя этой продукции. Так что продукция звена-поставщика является одновременно сырьем для звена-потребителя.

Звено-потребитель принимает решение о планировании своего производства исходя из того, что динамика цен на сырье (как функция времени) для своего производства ему известна: например, можно взять динамику цен предыдущих лет либо ориентировочно справиться у своего поставщика. Цена сырья входит в эксплуатационные расходы производства, и поэтому является инструментом регулирования и согласования планов звеньев. Получив свой план развития, звено-потребитель l предлагает его в качестве плана поставок звену-поставщику l-1. Звено-поставщик, зная динамику цен на сырье для своего производства, строит свой план развития и предлагает другую динамику цен на продукцию - сырье для звена-потребителя. Эта динамика цен соответствует минимальному значению функционала для звена-постав­щика l-1. Звено-потребитель l решает перепланировать развитие своего производства при новой динамике цен на сырье. При этом оно руководствуется минимальным значением функционала своего производства, после этого предлагает новый план поставок звену-поставщику. Этот итерационный процесс продолжается до тех пор, пока не будет достигнуто согласие поставщика и потребителя. Интересы народного хозяйства при этом учитываются также заданием некоторых внешних параметров (факторов).

Итак, оптимизация развития ЯТЭК сводится к поиску оптимального согласованного плана всех звеньев ЯТЭК.

Это только один из уровней оптимизации развития ЯТЭК. Другим, более низким, уровнем является оптимизация собственно ядерных энергетических установок (ЯЭУ) как элементов структуры звена сжигания топлива (звена ядерной энергетики), а также технологий и оборудования на предприятиях звеньев топливной базы. Разумеется, эта оптимизация должна проводиться в системе ЯТЭК. Так, ядерный реактор может обеспечить заданные ему энергетические характеристики при разных ценах на ядерное топливо (которое покупает ЯЭУ у топливной базы). При этом, если цена на ядерное топливо, которое продает топливная база, велика, то может оказаться выгодным обеспечить такую конструкцию (компоновку и т.д.) ядерного реактора и его режим работы, при которых потребление топлива было бы минимально (или, иначе, минимизировать функционал - приведенные затраты в строительство и эксплуатацию этой ЯЭУ), т.е. "переделать" ядерный реактор в сторону уменьшения потребления топлива данного вида, либо потреблять другое топливо. Но тогда и топливной базе не целесообразно работать "по-старому", коль скоро изменился спрос на топливо. Следовательно, нужно заново произвести оптимизацию развития топливной базы с учетом тех изменений, которые внесла ядерная энергетика (например, изменилось потребление топлива в ЯЭУ). Этот простой пример показывает, как влияют и изменяют структуру друг друга ядерная энергетика и ее топливная база. Эти итерационные изменения производятся до тех пор, пока не будет достигнуто "согласие", т.е. устойчивость в работе обеих систем.

Оптимизация развития системы производств (звеньев) ЯТЭК производится по критерию минимума интегральных приведенных (дисконтированных) затрат на строительство и эксплуатацию предприятий ЯТЭК на бесконечном интервале планирования.

Сформулируем задачу оптимизации лишь одного звена ЯТЭК. Для простоты будем считать, что звено потребляет один вид сырья и вырабатывает один вид продукции, поступающий на склад продукции. Со склада продукция отгружается заказчику в соответствии с планом поставок.

Однотипные предприятия оптимизируемого звена должны последовательно вводиться в строй в моменты t_j, , 0t_j<T; на конец планового периода T ввод предприятий, как правило, не предусматривается. Общее количество предприятий n+1; установленная мощность каждого из них Q_j.

Пусть капитальные затраты в каждое из предприятий зависят от его установленной мощности Q и вместе с приведенной к моменту пуска частью эксплуатационных расходов, не зависящей от загрузки предприятия, выражаются функцией f(Q). Естественно, что амортизационные отчисления должны подсчитываться с учетом непрерывного их использования в народном хозяйстве. Будем считать, что 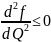при Q>0 и f(0)=0. Таким образом, f(Q) - вогнутая функция. Допустим, что оставшиеся эксплуатационные расходы пропорциональны текущей производительности предприятия. Причем положительный коэффициент пропорциональности с(t) не зависит от установленной мощности предприятия, но меняется с течением времени.

Тогда, выражение для критерия оптимизации может быть записано в виде

, (1.48)

где Е_н - коэффициент приведения (норматив дисконтирования); q(t) - суммарная текущая производительность введенных предприятий.

С помощью уравнения (1.48) затраты приводятся к начальному моменту планирования t=0 на основе формулы сложных процентов.

Функция приведения практически равна (для двух первых слагаемых разложения в ряд Тейлора равенство точное) множителю (1+Е_н)^-t в известной формуле приведения затрат.

Будем считать, что c(t) строго убывавшая функция времени; может быть разрывной. В любой момент рассматриваемого периода должен быть удовлетворен плановый спрос на продукцию предприятий q_c(t). Функцию q_c(t) будем считать строго возрастающей, она также может быть разрывной.

Если q_у(t) суммарная мощность установленная ранее момента t, а m(t) - складской запас, то должны выполняться неравенства

0q(t)q_у(t); (1.49)

m(t)0; (1.50)

Q_j0. (1.51)

Установленную в доплановый период t<0 мощность и начальный складской запас будем считать равным нулю. Тогда

, t_j-1<t<t_j; (1.52)

, (1.53)

причем t₀=0,t_n+1=T.

Таким образом, задача оптимизации звена ЯТЭК в этом простом случае сводится к поиску минимума функционала (1.48) на множестве ограничений (1.49) - (1.53). Оптимизации подлежат: число предприятий, моменты их ввода t_j, установленные мощности Q_j и план загрузки предприятий, т.е. график изменения суммарной текущей производительности введенных предприятий q(t).

Можно показать, что полный функционал ЯТЭК сводится к сумме функционалов отдельный звеньев З_l, если при оптимизации l-го звена в цепочке звеньев ЯТЭК коэффициент c(t) - удельные эксплуатационные расходы - представить суммой собственных удельных эксплуатационных расходов l-го звена и цены сырья, полученной при оптимизации звена l-1. Проводя оптимизацию звеньев цепочки ЯТЭК, последовательно переходя от звена к звену, можно получить оптимальный согласованный план по всем звеньям ЯТЭК. Увязку планов всех звеньев производят итерационно по параметрам спрос-цена.