2. Возможный порядок решения задачи оптимизации параметров тэу

Рассматривается порядок решения задачи оптимизации параметров технического устройства в «общем виде» (см. §1.4).

1. Задание значений внешних параметров .

2. Задание значений структурных (компоновочно-геометрических, предметных) параметров .

3. Задание значений числовых управляемых параметров (учет ограничений (1.10) производится в соответствии с выбранным способом.

4. Решение уравнений математической модели технического устройства; в случае нарушения ограничений, наложенных на рассчитываемые параметры, возврат к п. 3 (учет ограничений (1.11) или действия при их нарушении зависят от выбранного способа).

5. Расчет значений целевой функции и возврат к п.3, пока значения оптимизируемых управляемых параметров не совпадут на двух последовательных шагах спуска с заданной точностью.

6. Если требуется оптимизация структурных (предметных) параметров, то возврат к п.2.

7. Если предполагается оптимизация при другом или других наборах значений внешних параметров, то возврат к п.1.

Эффективность решения задачи зависит как от способов учета ограничений (см. п.3 и 4), так и от математического метода оптимизации, в соответствии с которым устанавливаются значения управляемых параметров в п.3 на каждом шаге движения к точке минимума целевой функции.

2. Задача динамической оптимизации

В некоторых задачах атомной энергетики критерий качества (целевая функция), который необходимо минимизировать, имеет более сложную структуру по сравнению с целевой функцией , рассмотренной в §1.1. Значения этого критерия зависят от времени t, которое рассматривается в интервале [t₀, T], и определяются следующими факторами: набором известных функций y₁(t), y₂(t), …, y_p(t); набором функций u₁(t), u₂(t), …, u_n(t), вид которых подлежит определению в ходе решения задачи; значениями числовых параметров х₁, х₂, …, х_n, не зависящих от времени.

В таких ситуациях критерием качества является некоторый заданный функционал , где , , .

Ставится задача; найти вектор и вектор-функцию из условия

, (1.42)

при этом на и накладываются ограничения в форме системы равенств и неравенств вида (1.2), а также функциональных равенств и неравенств вида:

, i= (1.43)

, k= при t[t₀, T].

Такие задачи называют задачами динамической оптимизации.

Динамическая оптимизация – метод управления, при котором процесс не только поддерживается на оптимальном уровне в установившемся (стационарном) режиме, но и переход из одного режима в другой осуществляется наилучшим образом. Динамическая оптимизация имеет некоторое сходство со статической оптимизацией, однако она более сложна, так как связана с необходимостью определять функцию времени, а не отдельные величины.

Формулировка инженерной задачи подобного типа рассматривается далее в §1.9.

Методика решения таких задач существенно зависит как от вида функционалов Ф, F_i, G_k, так и от физического содержания задачи. В некоторых случаях сформулированную задачу можно приближенно заменить задачей математического программирования. Покажем, например, как это можно сделать в задаче с интегральным целевым функционалом:

(1.44)

и ограничениями вида

f_i(x₁,x₂,…,x_n)0, i= ,

u_minu(t)u_max, (1.45)

,

где T, u_min, u_max, C - заданные константы; y(t) - известная скалярная функция; u(t) - неизвестная скалярная функция. Ставится задача: найти функцию u^*(t) и вектор , обеспечивающие минимум функционалу Ф( ).

Зададим на отрезке [t₀, T] набор точек t₀, t₁,…, t_N и заменим приближенно интегралы интегральными суммами (например, используя один из методов численного интегрирования). Обозначим u_k=u(t_k), y_k=y(t_k), k= . В результате получим задачу об отыскании векторов и из условия минимума функции

(1.46)

с учетом ограничений

f_i(x₁,x₂,…,x_n)0, i= ,

u_minu_ku_max, k= , (1.47)

.

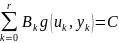Получили задачу математического программирования с неизвестными параметрами х₁, х₂,…, х_n, u₀, u₁,…, u_n.

Отметим, что число параметров существенно зависит от числа N точек t_k, выбираемых на отрезке [t₀, T].