2. Многоразмерная сложная оптимизационная задача

Данная задача является частной по отношению к предыдущей. Её целью является оптимизация минимальных температурных напоров (недогревов) в регенеративных подогревателях. Для упрощения постановки задачи минимальные температурные напоры в охладителях дренажа считаются неизменными. Будем считать также, что пароохладителя отсутствуют, что является характерным для турбоустановок на насыщенном паре.

При увеличении (уменьшении) недогрева t в каком-либо подогревателе, обогреваемом паром из отбора турбины, уменьшается (увеличивается) его теплообменная поверхность, что уменьшает (увеличивает) стоимость этого подогревателя и, как следствие, капитальные затраты К по станции в целом. С другой стороны, увеличение приводит к уменьшению электрической мощности турбогенератора, что можно учесть (метод замыкающих затрат) увеличением годовых затрат по станции в связи с необходимостью компенсировать недовыработку электроэнергии; в случае уменьшения t дополнительно отпущенная в сеть электроэнергия обусловит увеличение прибыли. Такой качественный анализ позволяет сделать вывод о том, что функциональная зависимость З (изменение годовых затрат по станции) от t является достаточно гладкой и имеет один минимум.

Обозначим совокупность оптимизируемых параметров данной зада­чи , где индексы соответствуют номерам поверхностных подогревателей системы регенерации; их количество равно L. Примем, что при изменении параметры пара в отборах турбины остаются постоянными, а меняются температуры нагреваемой воды на выходе из подогревателей.

Математическая постановка данной задачи может быть записана в виде, аналогичном (1.12) - (1.15),

(1.16)

, n= ; (1.17)

; (1.18)

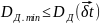. (1.19)

Здесь - наибольшее значение температурных напоров в теплообменниках, °С; Ц_l - удельная стоимость l–го теплообменника (исключая затраты на его транспортировку, монтаж и т.п.), руб./м²;F_l и F_lб - величина поверхности нагрева l–го подогревателя в варианте, характеризуемом некоторой совокупностью значений , и базовом, м².

Условие (1.19), отражающее требование недопустимости запаривания деаэратора (D_Д - расход греющего пара на деаэратор), может быть проверено заранее при t_lД=0 (lД - номер подогревателя, стоящего перед деаэратором), и в дальнейшем либо не приниматься во внимание, либо учитываться в одном из условий (1.18):

t_lД,mint_lД, (1.18а)

где t_lД,min- значение недогрева, обеспечивающее минимально допустимый расход греющего пара в деаэратор.

Учитывая необходимость многократного решения системы уравнений (1.17) и трудоемкость этого решения (даже при использовании ЭВМ), целесообразно зависимость получить в явном виде.

Тепловая мощность Q_l подогревателя l , в котором тепло передается только за счет конденсации пара,

(1.20)

где G_l - расход нагреваемой воды; С_рl - среднее значение изобарной теплоемкости в l-м подогревателе; t_вх.l, t_l - температура нагреваемой воды на входе и выходе; если питательная вода перед поступлением в l-й подогреватель проходит через охладитель дренажа, то t_вх.l- температура воды, нагретой в охладителе;t_sl - температура насыщения греющего пара. Величина теплообменной поверхности (см. уравнение (1.16) определяется на основе известного уравнения теплопередачи

(1.21)

Здесь k_l–коэффициент теплопередачи; t_лог.l=(t_sl-t_вх.l-t_l)/ln[(t_sl-t_вх.l)/t_l] –среднелогарифмический температурный напор.

С учетом (1.20) и (1.21), а также полагая, что изменением C_pl и k_l при вариациях можно пренебречь, перепишем уравнение (1.16) в виде

(1.16a)

Как следует из опубликованных результатов исследований зависимости , , ) с высокой точностью могут быть приняты линейными, т.е.:

(1.22)

(1.23)

(1.24)

здесь условно принято t₀=1.

Количество коэффициентов в уравнениях (1.22) - (1.24) равно (L+1)(2L+1). Их значения могут быть найдены методом наименьших квадратов после расчета определенного числа вариантов тепловой схемы турбоустановки, характеризующихся различными . Расчет одного варианта тепловой схемы означает решение системы уравнений (1.17) при заданных (выбранных) значениях . В числе рассчитываемых параметров находятся N_э^нт, G_l и t_вх.l.

Возможен и другой способ определения коэффициентов. Пусть мы имеем результаты расчета базового варианта тепловой схемы и еще L вариантов, в каждом из которых по сравнению с базовым изменено значение недогрева только в одном из подогревателей. Обозначим это новое значение недогрева в j-м подогревателе t_jн, а значение параметров в этом варианте - . Заметим, что в число рассчитываемых параметров наряду с другими войдут N_э^нт, и _вх. В этом случае определение искомых коэффициентов возможно с помощью формул. Эти формулы, например, для одного из уравнений (1.23) имеют вид

(1.25)

. (1.26)

На этом этапе задача оптимизации заключается в минимизации функций (1.16а) при учете (1.18) и (1.18а).

После подстановки в (1.16а) уравнений (1.22) - (1.24) легко осуществляется дифференцирование целевой функции по оптимизируемым параметрам, если того требует выбранный метод решения. Если таким методом является градиентный, то значения компонент градиента З могут быть вычислены по формулам

(1.27)