2. Особенности поверхности, описываемой целевой функцией

Рассмотрим функцию . В допустимой области изменения эта функция описывает некоторую поверхность, на которой возможны особые точки, описываемые далее. Пусть внутренняя точка допустимой области.

Функция имеет локальный минимум в точке , если для этой точки можно указать окрестность, полностью лежащую в допустимой области и такую, что для всех точек 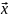из этой окрестности выполняется условие Аналогично определяется точка локального максимума.

Функция имеет глобальный минимум в точке , если для всех точек из допустимой области выполняется условие Аналогично определяется точка глобального максимума.

На рис. 1.1 показана функция Z(x), имеющая на отрезке [a,b] две точки локального минимума x₁ и x₃. Глобальный минимум достигается в точке x₃. Также эта функция имеет три точки локального максимума – в точках х=а, х=b и в точке х₂. Глобальный максимум достигается в граничной точке x=b.

Точка х₄ называется точкой локального перегиба.

Поверхности, задаваемые уравнениями Z(x₁,x₂,…,x_n)=C, где С - некоторая постоянная величина, называются поверхностями уровня функции .

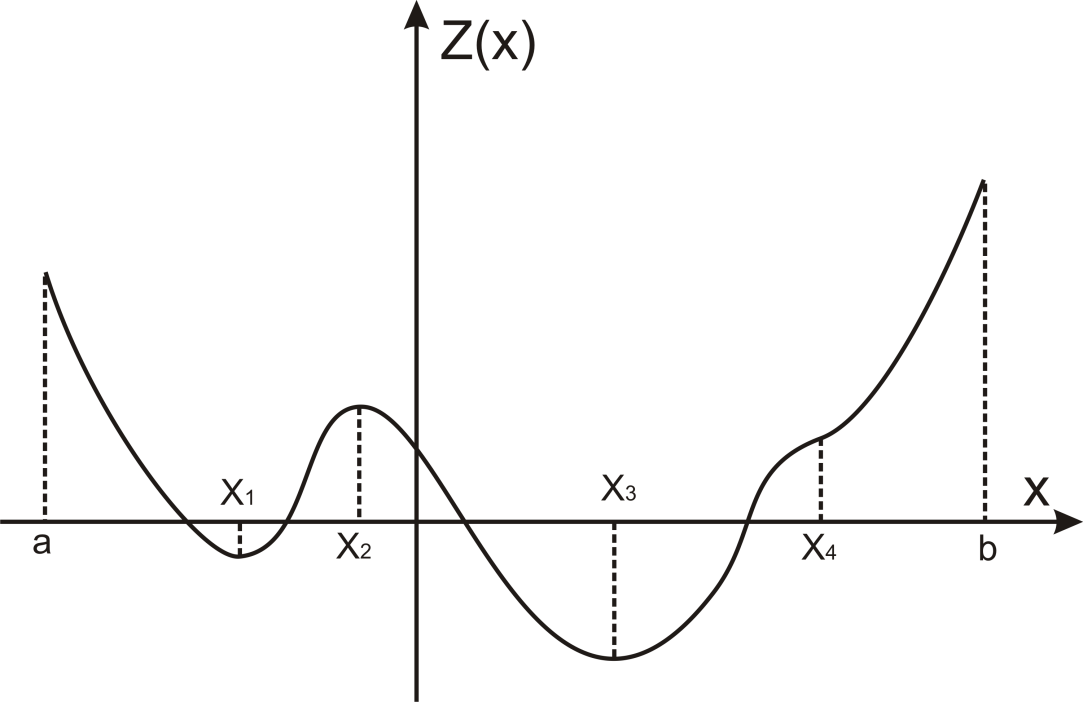
Рисунок 1.1

На рис. 1.2 показаны линии уровня функции двух переменных Z(x₁, x₂). Здесь, кроме точек локального и глобального минимума показана седловая точка (для n-мерной области – «точка типа седловой»)

Для этой точки частные производные равны нулю, но по направлению оси х₂ в ней достигается максимальное значение, а в направлении оси х₁ минимальное для некоторых диапазонов изменения х₂ и х₁ соответственно.

Рисунок 1.2

В точке типа седловой в n-мерной области для направлений некоторых координатных осей будет достигаться минимум целевой функции, а для направлений остальных осей – максимум (также в некоторых диапазонах изменения переменных ).

Вектор называется градиентом функции в точке . Важное свойство градиента: градиент в каждой точке ортогонален поверхности уровня и направлен в сторону возрастания функции.

2. Пример постановки оптимизационной задачи в общем виде

Теплоэнергетические установки (ТЭУ) предназначены для преобразования тепла в другие виды энергии (главным образом, в механическую и затем - в электрическую). К ТЭУ относятся тепловые и атомные электростанции.

В зависимости от конкретно решаемой задачи число оптимизируемых параметров в таких установках может быть велико. Обычно из общей задачи оптимизации ТЭУ выделяют ряд локальных задач с ограниченным (не более 7-10) числом оптимизируемых параметров.

Рассмотрим постановку задачи оптимизации параметров тепловой схемы турбоустановки АЭС. Решение задачи возможно, если заданы (или выбраны) значения некоторых параметров, которые не могут зависеть от работы данной установки, и поэтому называются внешними (или заданными). Совокупность этих параметров обозначим . К ним относятся прежде всего различные стоимостные показатели, отражающие сложившиеся взаимоотношения между предприятиями данной отрасли (энергетики) и межотраслевые: цены на строительные и монтажные работы и т.д. К внешним параметрам относятся также количество и характеристики вырабатываемой АЭС электроэнергии (мощность станции, график ее нагрузки - суточный, недельный, годовой и др.), параметры системы, обеспечивающей охлаждение конденсаторов (в том числе среднегодовая температура охлаждающей воды или окружающего воздуха).

Примем в нашем примере, что заданным условием оптимизации АЭС является базисный режим ее работы в течение _уст часов в году при постоянных мощности реактора Q_Р и параметрах теплоносителя на входе и выходе из него. Поскольку при этих условиях любое изменение какого-либо параметра в схеме станции приведет к изменению электрической мощности турбогенератора и мощности, расходуемой на собственные нужды, существенным является приведение всех рассчитываемых вариантов к одинаковому энергетическому эффекту, т.е. необходимо формальное обеспечение во всех вариантах равенства электрической мощности АЭС нетто и количества электроэнергии, отпускаемой с шин станции за определенный промежуток времени, например за год. Инструментом такого обеспечения может быть метод замыкающих затрат.

Оптимизируемыми или управляемыми параметрами в рассматриваемой задаче могут быть следующие:

1. Термодинамические параметры :

• начальное давление пара и величина его перегрева (если начальный перегрев пара предусмотрен);

• давление в конденсаторе (конечное давление пара);

• параметры промежуточных сепараторов и пароперегревателя (разделительное давление величины перегрева и минимальных температурных напоров в ступенях пароперегревателя и т.д.);

• температура питательной воды;

• параметры системы регенеративного подогрева (распределение подогрева между подогревателями, величины минимальных температурных напоров и др.).

2. Параметры определяющие конструктивно-компоновочный тип турбоустановки;

• число цилиндров в турбине;

• конструктивные характеристики последней ступени турбины, органов парораспределения;

• число сепараторов и (или) ступеней промежуточного пароперегревателя;

• соединение конденсаторов турбины (параллельное или последовательное), их характеристики;

• число и типы подогревателей системы регенерации (поверхностные, смешивающие), число параллельных ниток подогрева питательной воды, принцип регулирования давления в деаэраторе (постоянное, скользящее), расположение сливных (дренажных) конденсатных и питательных насосов, их типоразмеры и др.

Конструктивно-компоновочные параметры являются сугубо дискретными. Оптимизация может производиться только при условии задания . Путем сравнения результатов оптимизации при различных могут выбираться варианты с наилучшими конструктивно-компоновочными решениями.

Взаимное влияние оптимальных значений параметров неодинаково, что позволяет проводить их оптимизацию по группам, в первую очередь подлежат оптимизации те параметры, которые оказывают наибольшее влияние на оставшиеся. Так, например, распределение подогрева питательной воды по степеням , выбор оптимальных значений минимальных температурных напоров в подогревателях и охладителях дренажа может производиться в последнюю очередь (см. §1.5).

В соответствии с принятой методикой технико-экономических расчетов в энергетике в качестве критерия оптимальности или целевой функции принята величина приведенных годовых затрат; оптимальными значениями управляемых параметров являются те, которые обеспечивают минимум целевой функции:

. (1.6)

В рассматриваемой задаче в качестве целевой функции удобнее выбрать не абсолютное значение З, а ее изменение по сравнению с выбранным базовым (или исходным) вариантом:

. (1.7)

В этом случае в итоговом критерии учитываются только те составляющие, которые изменяются в зависимости от оптимизируемых параметров, что повышает точность расчетов. Если для приведения вариантов в сопоставимый вид выбран метод замыкающих затрат, то выражение для целевой функции можно записать в виде

, (1.8)

где (Е_Н+Е_К) - сумма коэффициентов отчислений, нормативных и на амортизацию, ремонт и обновление оборудования, год^-1; з^Э- замыкающие затраты на электроэнергию, руб./кВт∙ч; _уст - продолжительность использования установленной мощности, ч/год; К=К-К_б-изменение суммарной стоимости оборудования схемы турбоустановки; N_Э^НТ=N_Э^НТ-N_Эб^НТ=N_Э-N_СН- изменение электрической мощности турбоустановки, нетто; N_Э- изменение мощности турбогенератора; N_СН- изменение мощности, необходимой для собственных нужд станции, кВт.

Зависимость З от оптимизируемых параметров получить в явном виде, как правило, не представляется возможным; то же самое можно сказать и относительно зависимостей от оптимизируемых параметров К и N_Э^НТ, входящих в уравнение (1.8).

Их величины при заданных значениях оптимизируемых и внешних параметров рассчитываются с помощью уравнений, совокупность которых представляет собой математическую модель данной ТЭУ:

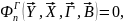n= (1.9)

Здесь N_Г - общее количество уравнений в системе, зависящее от принятых конструктивно-компоновочных решений (параметров ); - решение системы уравнений (1.9) - совокупность рассчитываемых или неуправляемых параметров (термодинамических, расходных, конструктивных и др.), в число которых входят и К и N_Э^НТ. Конкретный вид уравнений (1.9) зависит от принятых конструктивно-компоновочных характеристик схемы.

В систему (1.9) в общем случае входят:

• уравнения тепловых (энергетических) и материальных балансов элементов тепловой схемы;

• уравнения, отражающие приращение (уменьшение) термодинамических параметров в элементах схемы;

• уравнения (состояния, интерполяционные) для расчета одних параметров состояния по другим (например, энтальпии, теплопроводности и др. - по температуре и давлению);

• уравнения, описывающие процессы теплопередачи;

• уравнения для расчета конструктивных характеристик элементов схемы турбоустановки, показателей водного режима и др.

Совокупность уравнений, входящих в систему (1.9), зависит в каждом случае от целей конкретно решаемой задачи.

В общем случае на оптимизируемые и рассчитываемые параметры могут быть наложены ограничения в виде неравенств

(1.10)

(1.11)

В рассматриваемой задаче для параметров ограничения (1.10) могут быть заданы, например, для величины подогрева питательной воды в подогревателях, греющий пар для которых отбирается перед последней ступенью турбины или из холодной нитки промежуточного перегрева пара и в некоторых других случаях; разделительное давление в турбине может задаваться в пределах, определяемых влажностью пара на выходе из цилиндров высокого и низкого давления и т.д.

Неравенства (1.11) представляют собой уравнения, в общем случае, заданные не явным образом, и их учет должен производиться в процессе решения системы (1.9).

Примерами ограничений (1.11) могут быть:

• для термодинамических параметров - значение температуры подогрева воды в подогревателе перед деаэратором, приводящее к его запариванию (нулевому или отрицательному расходу греющего пара на деаэратор);

• для расходных параметров - максимальное значение греющего пара на одну деаэрационную колонку, максимальный расход воды на один насос и т.д.;

• для конструктивных параметров - максимальное значение теплопередающей поверхности одного подогревателя, минимальный диаметр труб в каком-либо теплообменнике или максимальный диаметр корпуса и т.д.

Таким образом, можно дать следующую формулировку рассматриваемой задачи: требуется определить такие значения управляемых параметров (возможно также и ), которые удовлетворяли бы ограничениям (1.9) - (1.11) и обеспечивали минимальное значение целевой функции (1.8). Заметим, что на основе сравнения постановки данной задачи (1.8) - (1.11) с постановкой задачи математического программирования (1.1) - (1.2) система уравнений (1.9), являющаяся по существу математической моделью ТЭУ, отнесена к уравнениям ограничения. Последнее замечание существенно, если иметь в виду решение данной задачи одним из методов математического программирования.

В случае, когда конструктивно-компоновочные решения определены или заданы и внешние условия зафиксированы, параметры и входят в значения коэффициентов уравнений (1.3), (1.4) и (1.6), и постановка рассматриваемой задачи упрощается:

, (1.12)

n= , (1.13)

(1.14)

. (1.15)

В некоторых случаях на основе предварительных расчетов целесообразно (и возможно) получение аппроксимационных зависимостей К( ) и N_Э^НТ( ), а следовательно, и зависимости целевой функции от в явном виде, что предоставляет большие возможности в выборе методов оптимизации.