1. Метод внутренних штрафных функций

Использование внутренних штрафных функций, также как и внешних, строится на основе задания функций ограничений. К ним предъявляются следующие требования :

а) они должны слабо влиять на исходную целевую функцию внутри допустимой области ограничений;

б) резко возрастать при приближении к границе этой области.

Наиболее часто в качестве внутренних штрафных функций используют обратные функции:

(4.5)

и логарифмические:

(4.6)

Параметр rдля внутренних штрафных функций выбирается из значений 0<r<1.

Особенностью метода внутренних штрафных функций является необходимость вычислений значений целевой функции по параметрам, находящимся строго внутри области. При выходе за ее пределы обратная функция принимает отрицательное значение и не выполняет свою «штрафную» функцию. Логарифмическая функция за пределами допустимой области не определена (логарифм отрицательного числа не имеет смысла).

2. Метод внешних штрафных функций.

При этом подходе функция подбирается так, чтобы выполнялись условия:

a) , т.е. i-ое ограничение выполняется;

б) .

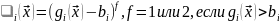т.е. внутри допустимой области штрафные функции равны нулю, а при удалении от границы допустимой области возрастают. Линейно (при f=1) или по параболе (при f=2)

Параметр r усиливает действие штрафных функций. Для внешних штрафных функций выбирают r≥1.

При использовании данного способа учета ограничений в методах оптимизации обычно принимают r=1. При достижении заданной точности его значение следует увеличить и продолжать движение к точке минимума из уже найденной точки при меньшем r. Вычисления прекращают, когда после увеличения r дальнейшее движение не превышает заданную точность.

На рис. 4.3,a и 4.4,а представлены изображения штрафных функций при f=1 и f=2 соответственно, а рисунки 4.3,б и 4.4,б иллюстрируют влияние параметра на вид вспомогательной функции F.

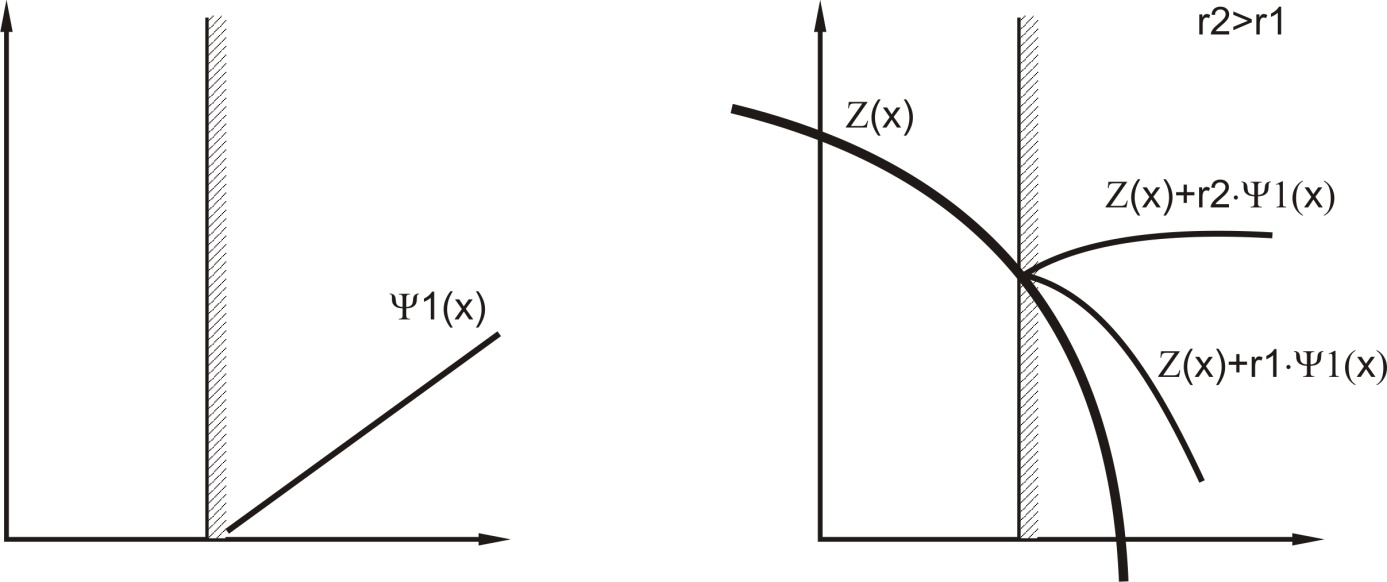
Рисунок 4.3,а Рисунок 4.3,б

Рисунок 4.4,а Рисунок 4.4,б

При использовании метода внешних штрафных функций оптимизируемые параметры могут принимать значения как внутри допустимой области, так и вне ее. Таким образом, проверка всех ограничений после каждого шага совершенно необходима для правильного определения значений штрафных функций. Заметим, что в точке за пределами допустимой области не все штрафные функции будут отличны от нуля.

4. Методы перебора вариантов

   1. Перебор на равномерной сетке

Рассмотрим задачу (1.1). Для простоты изложения метода предположим, что допустимая область представляет собой единичный гиперкуб, т.е. каждая сторона которого равна 1. Область поиска общего вида можно преобразовать в единичный гиперкуб путем замены переменных ; очевидно тогда .

В гиперкубе строим равномерную сетку с шагом h/M, образованную системой плоскостей , параллельных координатным плоскостям. Точки, образованные пересечениями этих плоскостей, назовем узлами. Всего получим (M+1)ⁿ узлов. Вычислим значения целевой функции в каждом из этих узлов.

Решением задачи будут координаты того узла, значение целевой функции в котором минимально. Для повышения точности расчета вокруг этого узла может быть построена новая сетка с меньшим расстоянием между плоскостями h.

Особенности практической реализации:

а) Рассмотренный метод является универсальным, так как может применяться для поиска глобального минимума невыпуклых функций и гарантирует (теоретически) определение точки минимума с требуемой точностью для всякой непрерывной функции.

б) Поиск точки минимума связан с организацией перебора точек n-мерной сетки; алгоритм такого перебора может быть громоздким.

в) Как уже отмечалось, для реализации каждого этапа метода (при выбранном расстоянии h между плоскостями сетки) требуется произвести L=(M+1)ⁿ вычислений значений функции. Так, если каждая сторона единичного гиперкуба делится на М=4, а число искомых переменных составляет n=10, то L=(4+1)¹⁰=9765625. Таким образом, реализация метода требует выполнения очень большого объема вычислений. В связи с этим метод перебора на равномерной сетке применяют, как правило, "за неимением лучшего" и для задач с числом оптимизируемых параметров не более 7.