2. Модификации алгоритмов безусловной минимизации

Пусть решается задача, постановка которой рассмотрена в §1.1 включающая в себя функцию (1.1) и ограничения (1.2а), (1.2б). В постановке задачи могут присутствовать уравнения математической модели, решение которых есть необходимый этап для расчета значений целевой функции.

Решение такой задачи можно найти на основе методов безусловной минимизации, если в соответствующих алгоритмах предусмотреть проверку ограничений после каждого шага спуска, от результата которой зависят дальнейшие действия. Такие действия достаточно апробированы для метода градиента и покоординатного спуска.

Эти способы сформулируем в виде двух правил.

1) Пусть в задаче ограничения заданы простыми неравенствами:

. (4.1)

Если в процессе поиска точки минимума оказались нарушенными одно или несколько ограничений из (4.1), то значения соответствующих параметров принимают равными их значениям на границе. Дальнейшая оптимизация проводится без их участия, пока не будут нарушены другие ограничения (способ организации движения по границам).

Иллюстрация этого способа для целевой функции от двух переменных дана на рис.4.1. Из точки k градиентным методом сделан шаг по направлению минимума и оказалось нарушенным ограничение . Далее минимизируется функция ) - вместо x₁ подставлено его значение на границе. После очередного шага оказалось нарушенным ограничение . Минимизация функции оказалась невозможной. Точка (k+2) - решение задачи.

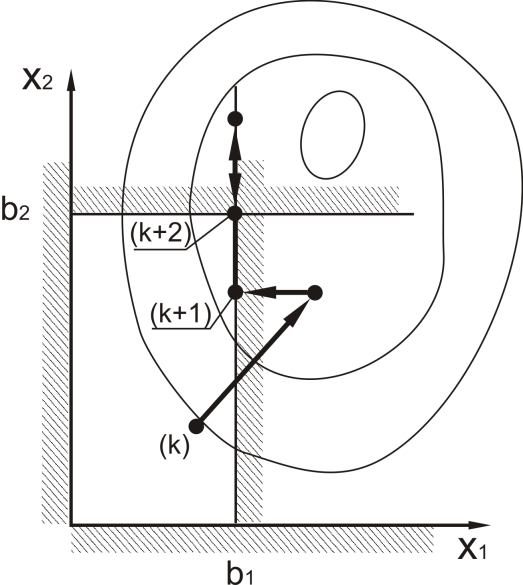
Рисунок 4.1

Способ, включающий проекцию точки и проекцию градиента на поверхность, описываемую различными ограничениями, описан в [5].

2)Пусть ограничения заданы в более общем виде:

. (4.2)

Если при поиске точки минимума оказались нарушены l ограничений из (4.2), l=1,2,...,p, p<m, то возврат в допустимую область параметров реализуется по направлению, противоположному вектору, определенному, как сумма градиентов тех функций ограничения, которые оказались нарушенными. Таким образом вектор возврата в допустимую область записывается как:

. (4.3)

Иллюстрация использования этого способа в комбинации с градиентным методом дана на рис. 4.2. В задаче есть только одно ограничение Выход за пределы допустимой области происходит по антиградиенту целевой функции , а возврат в область по антиградиенту функции ограничения Зигзагообразное движение вдоль границы может быть остановлено, когда векторы и с заданной точностью окажутся параллельными (с - количество шагов, сделанных до выполнения указанного условия). Далее находят решение задачи на одном из векторов, возможно более близкое к границе.

Необходимость неоднократного нахождения вектора возврата в допустимую область делает этот способ малоиспользуемым на практике даже в задачах с одним ограничением.

Рисунок 4.2

3. Методы штрафных функций

Одним из наиболее распространенных универсальных методов учета ограничений при решении задач оптимизации является метод штрафных функций, основная идея которого состоит в замене задачи минимизации функции с учетом ограничений задачей безусловной минимизации вспомогательной функции.

Пусть имеется целевая функция и ограничения в виде . Составим вспомогательную функцию:

, (4.4)

где r>0 - скалярный параметр, а - функция, зависящая от ограничений задачи и называемая "штрафной функцией".

При выборе вида функции и способа задания значений r существует два принципиально разных подхода.