6. Метод поиска по симплексу или s2- метод.

Данный метод является методом нулевого порядка и предназначен для решения оптимизационных нелинейных задач.

Термин «симплекс» здесь означает простейшую замкнутую геометрическую фигуру в n–мерном пространстве оптимизируемых переменных с прямыми ребрами и n+1 вершинами: треугольник в пространстве двух переменных, тетраэдр в пространстве трех переменных и т.д.

В названии этого метода можно обнаружить сходство с симплексным методом линейного программирования. Это сходство состоит в том, что зависимость целевой функции от оптимизируемых параметров внутри симплекса условно принимается линейной. В этом случае можно воспользоваться одним из основных положений метода для линейных задач: решение находится в одной из вершин симплекса. В рассматриваемом методе принимается, что вершина, в которой функция принимает наибольшее значение по сравнению с другими вершинами симплекса, находится дальше, чем остальные, от точки минимума исследуемой целевой функции.

Метод наиболее наглядно может быть представлен на примере задачи с безразмерными и равноценными оптимизируемыми параметрами. Начальный симплекс в этом случае может быть задан в виде правильной фигуры (расстояния между вершинами одинаковые и могут быть приняты равными единице: t=1) и с равнозначным расположением относительно координатных осей (биссектриса угла симплекса с вершиной в начальной точке параллельна или совпадает с биссектрисой координатного угла).

Для решения задачи необходимо задать координаты начальной точки: , а также точность определения координат точки минимума ε_х, с которой может сравниваться расстояние между вершинами симплекса t, и константа 0<α<1 для уменьшения параметраt.

Алгоритм метода представим состоящим из трех этапов.

1. Построение начального симплекса производится посредством расчета его координат вершин (кроме начальной) по формуле:

(3.12)

где k=1,2,...,n; ; t - расстояние между вершинами.

2. Спуск в районе точки минимума производится посредством выполнения следующих операций:

2.1 Рассчитываются значения целевой функции в вершинах начального симплекса .

2.2 Определяется номер вершины r с максимальным значением целевой функции. Вершина r должна быть отброшена, а новый симплекс построен при сохранении n оставшихся вершин и введения новой вершины с номером n+1, симметричной отброшенной относительно центра тяжести оставшихся вершин. Построение нового симплекса нецелесообразно, если достигнута заданная точность решения t≤ε_x. В этом случае за решение задачи может быть принята вершина с наименьшим значением целевой функции или любая из вершин, кроме, очевидно, вершины r.

2.3 Определение центра тяжести оставшихся вершин:

. (3.13)

2.4 Определение координат новой вершины:

. (3.14)

2.5 Подготовка нового шага спуска (новой итерации): вершине n+1 присваивается номер r (n+1=r) и вычисляется в ней значение целевой функции Z Далее вычисления должны повторяться, начиная с шага 2.2. Однако, при этом возможны такие ситуации:

• в новой вершине с номером r значение целевой функции снова стало максимальным: два симплекса начали переходить один в другого, т.е. движение к точке минимума прекратилось;

• симплекс стал вращаться вокруг одной из вершин.

Для того, чтобы обнаружить одну из таких ситуаций, рекомендуется ввести счетчики для каждой из вершин l_j, j=0,1,…,n. Начальное значение для всех счетчиков нулевое. При исключении какой-либо вершины из рассмотрения (вершины с номером r) значение ее счетчика обнуляется, а для всех остальных увеличивается на единицу. Когда значение какого- либо счетчика l_j>M (M=1,65n+0,05n²) производится уменьшение (редукция) размеров симплекса, т.е. уменьшение расстояния между вершинами симплекса t=α·t, в качестве начальной точки берется одна из вершин текущего симплекса, значения счетчиков обнуляются и расчеты возобновляются, начиная с шага 2.1.

Модификацией рассмотренного метода является метод деформируемого многогранника (симплекса). В этом методе координаты новой вершины симплекса нередко предполагается вычислять по формуле:

, (3.15)

где Θ – коэффициент деформации симплекса.

При Θ=1 имеет место нормальное отображение симплекса (формула становится аналогичной (3.14); при Θ>1 происходит растяжение симплекса, при -1<Θ<1 – сжатие симплекса. Возможно определение такого значения Θ, при котором величина целевой функции по направлению , будет минимальной. Но это означает существенное осложнение алгоритма метода. Нередко значение Θ выбирают из конечного числа фиксированных значений (например, 0,5; 1; 2), при которых значение целевой функции будет наименьшим. Наилучшие значения этих коэффициентов для каждой конкретной задачи могут быть установлены только эмпирически.

Критерием окончания процесса поиска минимума целевой функции методом деформируемого многогранника может быть следующий:

. (3.16)

В этом выражении - центр тяжести симплекса, координаты которого вычисляются по формуле:

, j=1,2,…,n. (3.17)

Выполнение условия (3.16) означает, что гиперплоскость последнего симплекса с заданной точностью можно считать параллельной гиперплоскости, касательной поверхности, описываемой Z . Решением задачи в этом случае может быть центр тяжести последнего симплекса .

Если задача решается в размерных координатах, то начальный симплекс может быть произвольным, а для каждой координаты желателен подбор весовых коэффициентов a_j, с учетом которых будет вычисляться центр тяжести вершин симплекса.

Отметим важную особенность метода поиска по симплексу и метода деформируемого многогранника: каждый новый шаг в направлении точки минимума требует вычисления целевой функции только один раз. По этому показателю эффективность этого метода превышает эффективность других рассмотренных методов.

Пример

Методом поиска по симплексу определить скорости теплообменивающихся сред w1 и w2 в прямоточном теплообменнике, при которых расчетные затраты на теплообменник З минимальны.

.

В этих уравнениях:

;

;

;

;

;

;

;

;

;

.

Исходные данные:

;

;

;

;

;

;

;

.

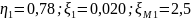Теплофизические свойства теплоносителей – определяются при давлении Р₁=1,2 МПа или Р₂=0,6 МПа и соответствующей средней температуре; материал труб – сталь 12Х18Н10Т, d=14 мм, ; сопротивление оксидных пленок и отложений

Ограничения:

Первое из приведенных ограничений означает, что отношение скоростей w2/w1 (w2 – скорость теплоносителя, омывающего трубный пучок снаружи) не может быть больше значения, определяемого наиболее плотным расположением труб. Коэффициент 0,66 рассчитан для труб с наружным диаметром 16 мм, толщиной стенок 1 мм и шагом в треугольной решетке, равным 1,35d_н.

Для учета ограничений применим метод внешних штрафных функций.

Выберем точку для построения начального симплекса w1=7, w2=2.

Координаты остальных двух вершин начального симплекса считаются по формулам (3.12). Параметр t=1.

Расчет значений новой целевой функции, включающей штрафные функции, производится по формуле:

,

где

Перед расчетом З_н определяется значение коэффициента теплопередачи k, используемое в формуле для З_н._.

Для того, чтобы значения штрафных функций были соизмеримы со значением целевой функции З, начальное значение скалярного параметра r принято равным 10⁵.

Значения целевой функции в вершинах начального симплекса:

З_н(7;2)=850350;

З_н(7,97; 2,26)=1369820;

З_н(7,26; 2,97)=999454.

Из трех значений отбрасываем вершину с максимальным значением и вычисляем согласно (3.13) центр тяжести оставшихся вершин: (7,13; 2,49).

Определяем координаты новой вершины по формуле (3.14):

w1=7,13+(7,13-7,97)=6,29;

w2=2,49+(2,49-2,26)=2,72.

Значение целевой функции в новой вершине вычисляем в соответствии с тем, нарушены ли ограничения:

З_н (6,29; 2,72)= 648602.

У нового симплекса максимальное значение З_н в вершине с координатами (7,26; 2,97).

При дальнейших вычислениях происходит движение симплекса, показанное на рис. 3.7. Направление движения определяется принятыми стоимостными характеристиками, при которых оказывается целесообразным уменьшение скоростей теплоносителей (уменьшение расхода электроэнергии на перекачивающие насосы) и увеличение теплообменной поверхности.

При скоростях теплоносителей w1=1,5-3 м/с и w2=0,8-1,6 м/с движение симплекса прекращается. В соответствии с алгоритмом метода принимаем новое значение параметра t=0,4 и строим симплекс меньшего размера на вершине «старого» симплекса с наименьшим значением целевой функции З_н.

Начальное движение нового симплекса также отображено на рис.3.7.

W1

W2

1369820

999454

850350

648602

566293

484777

424143

368071

317362

286074

242935

239627

196095

244394

W1=6

w2/w1=0,66G2/G1*ρ1/ρ2

Рисунок 3.7