4. Метод покоординатного спуска

Метод покоординатного спуска относится к методам нулевого порядка, так как его реализация не требует вычисления производных целевой функции. В этом методе в качестве направлений спуска (см. уравнение 3.2) берутся поочередно направляющие векторы координатных осей:

,

где .

Величина шага h_k при каждом спуске определяется также, как и в методе наискорейшего спуска. Таким образом, траектория спуска представляет собой ломаную линию, звенья которой параллельны координатным осям (рис. 3.6, с. 56).

Алгоритм метода представляет собой последовательность из n одномерных оптимизационных задач. Так что спуск из точки k в точку k+1 состоит из n (по числу оптимизируемых параметров) полушагов. Задача на каждом из полушагов заключается в нахождении точки минимума на одном из направлений :

, где Δx_j - алгебраическое приращение j-ой координаты, j=1,2,...,n.

Алгоритм метода легко программируется.

Надо иметь в виду, что гарантия сходимости метода дается только для дифференцируемой функции. При отсутствии дифференцируемости метод может остановиться в неоптимальной точке. В качестве геометрической иллюстрации на рис. 3.5 показано, что спуск в направлениях не приводит к уменьшению значения целевой функции и в результате итерации преждевременно останавливаются. Это объясняется наличием оврага, вызванного недифференцируемостью функции. Такой овраг, в частности, будет иметь место при решении задачи условной минимизации с учетом ограничений с помощью линейных внешних штрафных функций (см. §4.3.2).

Рисунок 3.5

Пример

Методом покоординатного спуска сделать несколько шагов по направлению к точке минимума целевой функции, в которой оптимальны значения минимальных температурных напоров в двух подогревателях высокого давления (ПВД) паротурбинной установки (ПТУ) К-1200-6,8/50.

Постановка задачи оптимизации минимальных температурных напоров в подогревателях системы регенерации теплоты ПТУ в общем виде описана в параграфе 1.5. Постановка такой же оптимизационной задачи для ПТУК-1200-6,8/50 и ее решение даны в [4]. В этой задаче в математическом выражении целевой функции З (руб/год) - изменение годовых приведенных затрат по сравнению с некоторым «базовым» вариантом, учитывалось, что при изменении изменяются площади теплообменной поверхности в подогревателях и электрическая мощность, вырабатываемая турбогенератором. Стоимости каждого подогревателя записывались в виде суммы постоянной составляющей и переменной, значение которой пропорционально площади теплообменной поверхности подогревателя F

где - удельная стоимость поверхности, i=1,2 – номер ПВД (меньший номер для подогревателя с наибольшим давлением греющего пара).

Поверхность нагрева в подогревателе состоит из поверхности зоны конденсации греющего пара и поверхности зоны охлаждения конденсата.

Площадь поверхности зоны конденсации греющего пара рассчитывалась по уравнению теплопередачи:

,

где – тепловая мощность и коэффициент теплопередачи в зоне конденсации греющего пара; – средний температурный напор, рассчитываемый как среднелогарифмический.

Изменением поверхности нагрева в зоне охлаждения конденсата в рассматриваемой задаче пренебрегалось. При упрощении выражения для целевой функции использовалось правило неизменности положения точки ее минимума при прибавлении или вычитании некоторого постоянного значения.

Со всеми преобразованиями выражения для целевой функции и исходными данными можно познакомиться в [4].

Заменив обозначение критерия оптимальности на Z, а обозначения оптимизируемых переменных на х1 и х2, получим следующее выражение для целевой функции в рассматриваемой задаче:

.

Для определения относительной величины шага вдоль какой-либо координаты применим метод квадратичной аппроксимации.

Первый полушаг метода покоординатного спуска будем реализовывать вдоль оси Х1.

Аппроксимационный полином:

.

Формулы для расчета коэффициентов:

;

;

.

Приравняв производную полинома по х нулю и решив уравнение относительно х, получим:

.

Для решения задачи выберем начальную точку:

.

Расстояние между точками на оси Х1 для расчета коэффициентов аппроксимационного квадратичного полинома a0, a1, a2 примем равным 2 ( .

Тогда получим:

х10=1, х11=3, х12=5;

Z0=66,459, Z1=64,611, Z2=69,523;

а0=66,459, а1=-0,924, а2=0,845;

x1_ОПТ=2,55.

Теперь, приняв х1=2,55, выполним поиск x2_ОПТ (второй полушаг, вдоль оси Х2).

Х20=1, х21=3, х22=5;

Z0=68,296, Z1=64,053, Z2=65,053;

а0=68,296, а1=-2,122, а2=0,655;

x2_ОПТ=3,62.

Завершен 1 шаг метода покоординатного спуска.

На втором шаге уменьшим расстояние между точками, выбранными для построения аппроксимационного полинома в два раза ( ).

Первый полушаг второго шага:

х2=3,62;

х10=1,55, х11=2,55, х12=3,55;

Z0=64,439, Z1=64,106, Z2=65,694;

а0=64,439, а1=-0,333, а2=0,961;

x1_ОПТ=2,22.

Второй полушаг второго шага:

х1=2,22;

Х20=2,62, х21=3,62, х22=4,62;

Z0=64,014, Z1=63,921, Z2=64,523;

а0=64,014, а1=-0,093, а2=0,347;

x2_ОПТ=3,25.

Завершен 2 шаг метода покоординатного спуска.

На третьем шаге уменьшим расстояние между точками, выбранными для построения аппроксимационного полинома еще в два раза ( ).

Первый полушаг третьего шага:

х2=3,25;

х10=1,72, х11=2,22, х12=2,75;

Z0=64,089, Z1=63,851, Z2=64,211;

а0=64,089, а1=-0,476, а2=1,196;

x1_ОПТ=2,17.

Второй полушаг третьего шага:

х1=2,17;

Х20=2,75, х21=3,25, х22=3,75;

Z0=63,937, Z1=63,843, Z2=63,96;

а0=63,937, а1=-0,188, а2=0,422;

x2_ОПТ=3,22.

Итак, после трех шагов метода покоординатного спуска получили оптимальные значения температурных наборов:

.

График пошагового спуска для данного примера представлен на рисунке 3.6.

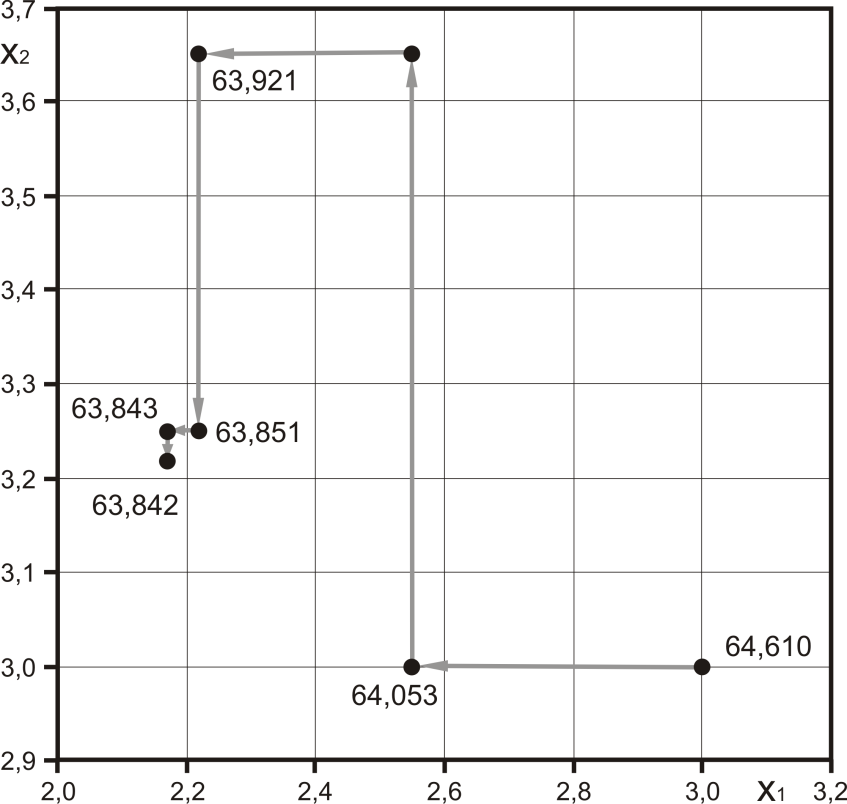
Рисунок 3.6