Метод наискорейшего спуска
Этот метод, по своей сути, есть модификация градиентного метода. Особые свойства этого метода обусловлены способом выбора шага спуска в направлении антиградиента (см. формулы (3.3) и (3.4)). Шаг выбирается из условия движения в выбранном направлении, пока функция убывает.
Координата любой точки в направлении антиградиента из точки может быть определена по формуле
где h – может принимать любое действительное значение. Значение h должно быть определено посредством минимизации функции одной переменной
.
Выберем метод одномерной минимизации – метод деления интервала пополам (метод трехточечного поиска на равных интервалах).
Алгоритм метода, совмещенный с определением границ интервала поиска, может быть следующим.
Пусть
известны координаты точки
и компоненты градиента в этой точке
.
1. Задается некоторое значение параметра h=hн и точность определения координат точки минимума εх.
2. Последовательно вычисляются координаты пробных точек по формуле
,
где
i=1,2,…
до тех пор пока
,
для i=1
.
3.
При значении i=I,
при котором
,
фиксируются границы интервала, внутри
которого расположен минимум функции
.
Координата
правой границы
.
Координата
левой границы
.
Точка
-
средняя на интервале, значение целевой
функции в ней известно
.
4.
Рассчитываются координаты точки справа
от
и
значение в этой точке целевой функции
.
Если
,
то граница нового (уменьшенного) интервала
и к шагу 4.
5. Рассчитываются координаты точки слева от
Если
,
то левая граница
остается без изменений, правая граница
,
, и к шагу 4.
6.
Левая граница
,
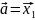правая граница
.
7.
Если
к шагу 9.
8.
и
к шагу 4.
9.
.
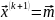Далее
определяется новое направление спуска
-
и
выполнение алгоритма спуска по направлению
возобновляется. Решением задачи будут
координаты точки, совпавшие с координатами
предыдущей:
.
Метод наискорейшего спуска обладает, как правило, более быстрой сходимостью по сравнению с градиентным методом с выбором шага по неравенству (3.6).
В то же время решение одномерной задачи на каждом шаге спуска является усложняющим обстоятельством.
Для успешного решения задачи как градиентным, так и методом наискорейшего спуска необходимо, чтобы целевая функция была ограничена снизу во всей исследуемой области и имела непрерывные производные по всем оптимизируемым параметрам.
При оптимизации управляемых параметров технических устройств или установок, когда требуется решение достаточно сложных математических моделей, возможны трудности с определением значений частных производных целевой функции. Численное определение этих значений возможно по формуле
.
Следует
иметь в виду, что такие вычисления могут
быть неустойчивыми, что связано с
накоплением вычислительной погрешности.
Шаг
не должен быть слишком малым.
Необходимо еще отметить, что и градиентный метод с выбором шага по неравенству (3.6) и метод наискорейшего спуска могут обеспечить сравнительно быстрый выход в район минимума, но далее сходимость может быть медленной. Большая эффективность может быть достигнута при использовании на втором этапе какого-либо другого метода.
Пример
Методом наискорейшего спуска сделать 1-2 шага в направлении минимума целевой функции (3.11) из примера 1:
.
Выберем значения оптимизируемых переменных в начальной точке:
.
и
относительную величину пробного шага
(такое значение объясняется малыми
величинами частных производных целевой
функции – см. далее).
Направление спуска к минимуму, как и в градиентном методе, противоположно направлению градиента целевой функции
.
После подстановки координат начальной точки получены следующие значения компонент градиента:
.
Для определения значения шага h1 в направлении антиградиента от начальной точки до точки минимума в выбранном направлении, применим один из методов одномерной минимизации – метод деления интервала пополам, иначе метод трехточечного поиска на равных интервалах.
Для определения интервала сделаем несколько шагов в направлении антиградиента.
Получим координаты этих точек:
Z(364; 354,4)=0,5991524
Целевая функция убывает.
Z(388; 368,8)=0,5990706
Целевая функция убывает.
Z(412; 383,2)=0,5991978
Целевая функция возросла, следовательно, границами для интервала метода трехточечного поиска будут координаты точек: (364; 354,4) и (412; 383,2).
Координаты средней точки (388; 368,8). Сравнивая значения целевой функции в серединах полученных отрезков Z(376; 361,2)=0,5990856 и Z(400; 376)=0,5991079, определяем следующий интервал: между точками (376; 361,6) и (400; 376).
Средняя точка остается той же (388; 368,8).
Z(
)=0,5990829
Z(
)=0,5990716
Минимум по данному направлению в точке (388; 368,8):
.
Вычисляем новое значение градиента:
.
Относительную
величину шага берем
,
т.к. величины компонент градиента
маленькие.
Z(389,9;359,6)=0,5990546
Значение целевой функции уменьшилось.
Z(391,8; 350,4)=0,5990515
Значение целевой функции уменьшилось.
Z(393,7; 341,2)=0,5990615
Значение
целевой функции увеличилось. Следовательно,
в качестве интервала для трехточечного
поиска минимума в данном направлении
берем интервал между точками
и (393,7; 341,2).
Средняя точка (391,8; 350,4)
Проверяем значения справа:
Z(392,8; 345,9)=0,5990548 - значение целевой функции увеличилось;
и слева
Z(390,9; 355)=0,5990514 - значение функции уменьшилось.
Можно считать это значение точкой минимума с относительной точностью
График пошагового спуска для данного примера представлен на рисунке 3.4.
Рисунок 3.4