2. Метод градиента

Метод градиента является легко доступным и хорошо алгоритмизируемым. Поэтому он является одним из самых распространенных методов безусловной минимизации.

Метод градиента является методом первого порядка. Его расчетная формула имеет вид:

(3.3)

Она получается из (3.2) при (направление антиградиента). Учитывая, что и , получаем координатную запись формул градиента:

;

; (3.4)

…………………………

.

На рис. 3.3 (стр. 47) показана геометрическая иллюстрация метода градиента для случая n=2. Траектория спуска представляет собой ломаную линию, звено которой, исходящее из точки ортогонально линии (или поверхности) уровня, проходящей через эту точку.

Возможны следующие способы выбора шага h_k.

Первый способ.

Пусть заданы величины h> 0, 0 <<1, постоянные для всех итераций. На (k+1)-й итерации, т.е. при определении координат (k+1)-й точки на основе уже известных координат k-й точки, выполняются следующие действия:

1) h_k=h - задание начального шага.

2) - вычисление координат пробной точки.

3) Проверка условия убывания

(3.5)

Если неравенство выполнено, спуск произошел: полагаем

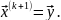
Если неравенство не выполнено, рекомендуется уменьшить шаг, т.е. заменить h_k на h_k и вернуться к п. 2.

Таким образом, на каждой итерации шаг выбирается из условия убывания функции в точках последовательности .

Заметим, что убывание последовательности еще не гарантирует сходимости последовательности к точке минимума.

Проще говоря, спуск маленькими шагами делает процесс нахождения минимума долгим, а при больших шагах точку минимума можно "проскочить".

Этот способ требует, как правило, большое число итераций (шагов спуска) и не гарантирует нахождение точки минимума.

Второй способ.

Зададим величины h>0, 0<<1, 0<γ<1, постоянные для всех итераций. На (k+1)-ой итерации выполняются следующие действия.

1) h_k=h - задание начального шага.

2) - вычисление координат пробной точки.

3) Проверка условия убывания

. (3.6)

Если неравенство выполнено, произошел спуск, полагаем . В противном случае рекомендуется заменить h_k на ∙h_k и вернуться к п. 2.

Неравенство (3.6) может быть получено из разложения функции в ряд Тейлора в окрестности точки ; коэффициент γ в определенной мере компенсирует отброшенные слагаемые. Значения γ,  выбираются эмпирически с учетом специфики задачи. В ряде случаев можно рекомендовать γ =0,7; =0,5 .

Алгоритм метода градиента

Начальный этап. Задать начальную точку и константу точности .

Основной этап. Пусть известна точка .

1) Положить и найти h_k одним из рассмотренных способов.

2)

3) Применить один из критериев окончания итераций. Например, если условие выполнено, то остановиться, если же нет, то заменить k+1 на k и перейти к шагу 1.

Доказывается, что сходимость метода обеспечивается при следующих условиях:

1) функция ограничена снизу в допустимой области;

2) все производные непрерывны в допустимой области;

3) шаг спуска h_k выбирается из условий (3.5) или (3.6).

Пример

Градиентным методом определить оптимальные по тепловой экономичности подогревы воды в двух подогревателях, смешивающего типа, составляющих систему регенерации теплоты паротурбинной установки без промежуточного перегрева пара турбины.

Получение формулы для критерия оптимальности.

Пронумеруем подогреватели: 1 - с наибольшим давлением греющего пара, 2 - с наименьшим давлением греющего пара.

Из уравнений теплового баланса для этих подогревателей можно получить формулы для расчета расхода греющего пара в долях расхода пара на турбину:

(3.7)

где удельная теплота, отдаваемая греющим паром в подогревателе с номером i (разность энтальпий пара на входе и конденсата пара на выходе смешивающего подогревателя); - подогрев (разность энтальпий) воды в этом подогревателе; i=1 или 2.

Энергетический баланс рассчитываемой ПГУ может быть представлен как равенство теплоты подведенной к ПТУ единицей расхода пара, сумме выработанной этим паром электрической энергии w_э и теплотыq_к, отводимой в конденсаторе турбины:

(3.8)

где - расход пара в конденсатор, отнесенный к расходу пара на турбину, удельная теплота (разность энтальпий), отдаваемая паром в конденсаторе.

Тогда критерий оптимальности – электрический к.п.д., определяющий тепловую экономичность турбины, можно записать в виде:

η_э , (3.9)

где , - энтальпия пара, подводимого к турбине, - энтальпия воды на выходе из подогревателя 1, с которой она поступает в паропроизводительную установку, , - энтальпия воды на входе в систему регенерации теплоты (на входе в подогреватель 2).

После подстановки в (3.9) выражений (3.7) и (3.8) и некоторых преобразований получим:

η_э (3.10)

Таким образом, требуется определить такие подогревы 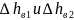, при которых ηэ будет иметь максимальное значение. Это условие будет выполнено, если вычитаемое в (3.10) будет минимально.

В целях более наглядной демонстрации метода оптимизации примем, что удельная теплота пара и не зависит от оптимизируемых переменных . Тогда, взяв числовые значения из расчета выбранной ПТУ, переобозначив оптимизируемые параметры как х1 и х2, получим для рассматриваемого примера следующий критерий оптимальности (целевую функцию):

(3.11)

который нужно минимизировать.

Размерность констант и оптимизируемых параметров в (3.11) – килоджоули на килограмм (кДж/кг); критерий Z – безразмерный.

Применение градиентного метода.

В пространстве оптимизируемых переменных выберем начальную точку с координатами

.

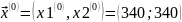Значение целевой функции в начальной точке .

Частные производные целевой функции¹:

;

.

Значения компонент градиента в начальной точке:

Значение модуля градиента:

будет использовано в алгоритме определения относительного шага h.

_{Начальное значение относительного шага спуска в направлении, противоположном градиенту} , примем (порядок этой величины определяется малыми значениями частных производных), константу в неравенстве (3.6) для определения шага , коэффициент _{уменьшения шага α=0,5.}

Первый шаг: Координаты точки будем вычислять в соответствии с алгоритмом на 41 с.

h=h_н

Неравенство (3.6) не выполняется, следовательно уменьшаем шаг в соответствии с коэффициентом α.

h=0,5h_н=210⁶

Неравенство выполняется, следовательно принимаем

Второй шаг:

h=h_н=410⁶

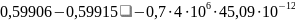
Неравенство не выполняется, аналогично уменьшаем шаг до 2 :

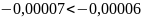
Неравенство выполняется, следовательно:

Третий шаг:

h=h_н=410⁶

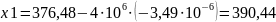
Неравенство не выполняется, аналогично уменьшаем шаг до 2 :

Неравенство не выполняется, следовательно, уменьшаем шаг еще в 2 раза:

Неравенство не выполняется, следовательно, уменьшаем шаг еще в 2 раза:

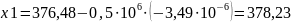
Неравенство выполняется, следовательно:

Достигнута относительная точность определения целевой функции:

Точность определения оптимизируемых параметров:

или относительная точность

График пошагового спуска для данного примера представлен на рисунке 3.3. Для достижения большей точности вычислений следует продолжить предложенный алгоритм.

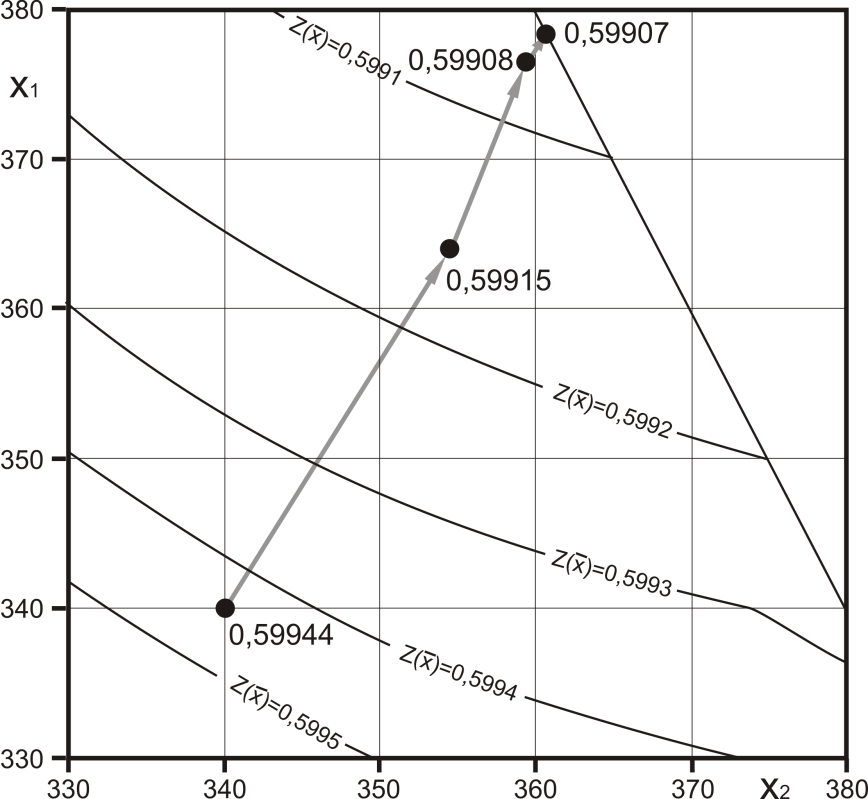
Рисунок 3.3