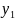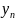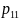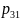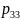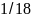Занятие № 7 Многомерные случайные величины (случайные векторы) и их характеристики.
1°. Понятие случайного вектора.
Иногда, в случайных экспериментах, приходится отслеживать значения нескольких случайных величин. Например, при стрельбе по мишени случайными будут обе координаты точки попадания. При подбрасывании 2 – х кубиков можно интересоваться, например, тремя СВ: очками, выпавшими на каждом из них, и ещё их суммой или разностью. Примеров можно привести очень много.
Ниже мы
рассмотрим двумерный
случай,
который с одной стороны более нагляден
и технически менее трудоёмок, а с
другой – включает в себя все основные
особенности многомерных
СВ. Итак, две случайные величины
 ,
заданные на одном
и том же
вероятностном пространстве, мы будем
рассматривать как упорядоченную пару
,
заданные на одном
и том же
вероятностном пространстве, мы будем
рассматривать как упорядоченную пару
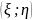 и называть двумерной
случайной величиной
или двумерным
случайным вектором.
Геометрически ДСВ интерпретируется
как случайная
точка с
координатами
на плоскости в системе прямоугольных
координат
и называть двумерной
случайной величиной
или двумерным
случайным вектором.
Геометрически ДСВ интерпретируется
как случайная
точка с
координатами
на плоскости в системе прямоугольных
координат
 ,
или как радиус
– вектор этой
точки.
,
или как радиус
– вектор этой
точки.
Многие
основные понятия, связанные со
случайной величиной переносятся и
на многомерный случай. Так, совместной
функцией распределения
ДСВ называется функция двух переменных
 ,
определенная на всей плоскости, и
заданная соотношением
,
определенная на всей плоскости, и
заданная соотношением

Иначе говоря, для
каждой пары значений
 −
это вероятность того, что случайная
точка
−
это вероятность того, что случайная
точка
попала в квадрант с вершиной , изображенный ниже на рисунке.




 •
•
 О
О

Совместная функция
распределения
 обладает следующими общими свойствами:
обладает следующими общими свойствами:
 не убывает по
каждой переменной;
не убывает по
каждой переменной;



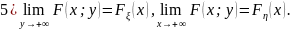
Здесь
 функции распределения случайных
величин
соответственно. Их называют маргинальными
распределениями. Таким образом, по
совместной функции распределения
можно определить функции распределения
отдельных компонент, но обратное,
вообще говоря, неверно.
функции распределения случайных
величин
соответственно. Их называют маргинальными
распределениями. Таким образом, по
совместной функции распределения
можно определить функции распределения
отдельных компонент, но обратное,
вообще говоря, неверно.
2°. Дискретная двумерная случайная величина.
ДСВ
называется дискретной
(ДДСВ), если и
являются дискретными случайными
величинами. Если при этом
 принимает значения
принимает значения
 ,
а
,
а
 значения
значения
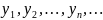 ,
то вероятности
,
то вероятности

представляют собой совместный закон распределения ДДСВ . Если множества возможных значений обеих величин конечно, то закон распределения можно представить в форме таблицы с двумя входами:
|
|
|
|
. . . |
|
|
|
|
|
|
. . . |
|
|
|
|
|
|
. . . |
|
|
|
|
|
|
. . . |
|
|
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
|
|
|
|
|
. . . |
|
|
|
|
|
|
. . . |
|
|
В последней строке этой таблицы записан закон распределения СВ , а в крайнем правом столбце – закон распределения СВ . Эти законы также носят название маргинальных.
Величины
считаются независимыми,
если для любых допустимых
 ,
верно, что
,
верно, что

Пример 2.1
Симметричный
игральный кубик подбрасывают 2 раза.
Пусть
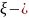 число очков, выпавшее первый раз,
число очков, выпавшее второй раз и
число очков, выпавшее первый раз,
число очков, выпавшее второй раз и
 .
Составить таблицу закона распределения
ДДСВ
.
Составить таблицу закона распределения
ДДСВ
 и маргинальных законов.
и маргинальных законов.
 Решение.
Прежде всего, отметим, что при
фиксированном значении
,
значение
Решение.
Прежде всего, отметим, что при
фиксированном значении
,
значение
 однозначно
определятся тем, сколько очков выпало
во второй раз, т. е. значением
.
Поэтому,
однозначно
определятся тем, сколько очков выпало
во второй раз, т. е. значением
.
Поэтому,
 .
Последняя вероятность либо равна 0
(если
.
Последняя вероятность либо равна 0
(если
 ),
либо равна
),
либо равна
 ,
что соответствует вполне определенному
исходу при подбрасывании кубика
дважды. Теперь можно составить таблицу
закона распределения:
,
что соответствует вполне определенному
исходу при подбрасывании кубика
дважды. Теперь можно составить таблицу
закона распределения:
|
2 |
3 |
4 |
5
|
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
1 |
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
|
2 |
0 |
|
|
|
|
|
|
0 |
0 |
0 |
0 |
|
3 |
0 |
0 |
|
|
|
|
|
|
0 |
0 |
0 |
|
4 |
0 |
0 |
0 |
|
|
|
|
|
|
0 |
0 |
|
5 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
0 |
|
6 |
0 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Как и следовало ожидать, в правом крайнем столбце мы получили распределение СВ числа выпавших очков при первом броске, а в нижней строке − распределение суммы. ∎