Многоугольник распределения св

г) функция распределения на разных участках задается по – разному, поэтому её аналитическое выражения будет выглядеть так

В соответствие с этим её график выглядит так:

0 1 2 3 4

График функции распределения св

д)

е) лучше вычислять, используя формулу : = Следовательно, среднеквадратич- ное отклонение ;

ж) , так как события и несовместны. ∎

Пример 2.2 Вычислить мат. ожидания и дисперсии для распределений 1* − 5* .

Классическое распределение:

арифметического квадратов значений СВ . Итак,

Бернуллиевская величина:

Итак, .

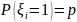Биномиальное распределение. Здесь проще всего заметить, что если СВ распределена по биномиальному закону, то её можно представить в виде суммы независимых одинаково распределенных СВ Бернулли: , где и В таком случае, по свойству математического ожидания, получим

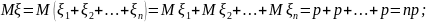
Таким образом, , .

Распределение Пуассона:

Следовательно,

Геометрическое распределение:

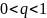, то данный степенной ряд сходится и его сумму 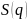можно интегрировать, и интеграл от неё равен сумме интегралов членов ряда. Иначе говоря,

Замечание. Иногда «геометрическое распределение» начинают с , а не 1. То есть распределение имеет вид: В этом случае ответы несколько изменяются. Именно,

Пример 2.3 Симметричный игральный кубик подбросили дважды. Написать ряд распределения СВ «сумма выпавших очков».

Решение. Пусть первый раз выпало . Тогда 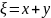, причем порядок здесь важен! Вероятность выпадения любой комбинации равна . Теперь подсчитаем возможные значения и сколько соответствующим значениям благоприятствует комбинаций ( в скобках):

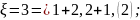
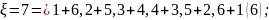
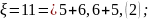
Ряд распределения имеет вид

	2	3	4	5	6	7	8	9	10	11	12

По этим вероятностям мы можем вычислить вероятности, вообще говоря, любых других событий, связанных с данной СВ. Например, вероятность того, что сумма очков окажется четной, будет равна

Д/З

Задача (ряд и функция распределений)

Построить ряд распределения и функцию распределения для пунктов 1*) при , ; 2*) , ; 3*) ; 6*) , , .

Задача (мат. ожидание числа очков)

Игральный кубик подбросили 1 раз. Найти мат. ожидание числа выпавших очков. Ответ: 3,5.

Задача (мат. ожидание суммы числа выпавших очков)

Игральный кубик подбросили 100 раз. Найти мат. ожидание суммы выпавших очков. Ответ: 350. (Указание: воспользоваться тем, что мат. ожидание суммы СВ равно сумме мат. ожиданий слагаемых, и результатом предыдущей задачи.)

Задача (несимметричный кубик)

Несимметричный кубик устроен так, что вероятности выпадений числа очков следующие: 1 – 0,1, 2 – 0,3, 3 – 0,2, 4 – 0,1. Каковы вероятности выпадения 5 или 6 очков, если известно, что матожидание числа выпавших очков 3,3. Ответ: .

Задача (изъятие бракованного транзистора)

В коробке находятся 8 транзисторов, из которых 3 бракованных. Последовательно и безошибочно проводят тестирование данных транзисторов, пока не обнаружится первый неисправный. Найти мат. ожидание числа транзисторов, прежде, чем обнаружат первый неисправный.

Решение. СВ число извлеченных транзисторов, до первого неисправного. Исправных транзисторов 5. Значит, . Найдем соответствующие значения вероятностей: , , . Итак,