Занятие № 5 Понятие случайной величины. Дискретные случайные величины и их характеристики.

1°. Общее понятие случайной величины.

Во многих вопросах, связанных с вероятностями событий, интересуются не столько самим событием, сколько определенными величинами, сопутствующими появлению события. Поскольку сами события, как правило, случайны, то и эти величины носят случайный характер. Например, при подбрасывании монеты интересуются не выпадением «герба» как такового, а сколько раз он выпал; интересуются не рождением мальчика или девочки, а, скажем, сколько тех и других родилось за год; при подбрасывании игральных кубиков могут интересоваться суммой выпавших очков и так далее…

Невозможно перечислить специфику тех случайных чисел, которые могут вызывать интерес в связи со случайными экспериментами. Поэтому принято случайной величиной считать функцию, заданную на пространстве элементарных событий. Таким образом, случайная величина функция элементарного события. Однако не всякую такую функцию принято считать случайной величиной (далее – СВ). Здесь надо иметь в виду следующее:

если пространство не более, чем счетно, то СВ считается любая функция;

если пространство несчетно, то СВ считаются лишь так называемые измеримые функции, то есть такие, что множество Иначе говоря,

Замечание. Множество называется счетным, если его элементы можно перенумеровать числами натурального ряда. Проще говоря, вытянуть в последовательность . Множество не более, чем счетно, если оно либо конечно, либо счетно. Множество, не являющееся таковым, называется несчетным. Типичный пример несчетного множества – совокупность всех действительных чисел. ∎

Законом распределения СВ называется всякое правило, согласно которому можно находить вероятности всевозможных событий, связанных со случайной величиной. Например, вероятность с которой она принимает конкретные значения или, скажем, попадает в заданные промежутки и т. п. Если СВ имеет данный закон распределения, то говорят, что «она распределена по этому закону» или же «подчиняется этому закону распределения».

Наиболее общей формой закона распределения является функция распределения, представляющая собой вероятность события, заключающегося в том, что случайная величина приняла значения меньшие, чем . Итак, функция распределения определена и

Функция распределения любой случайной величины обладает рядом общих свойств:

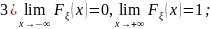
непрерывна слева;

2°. Дискретные случайные величины и их характеристики.

Случайная величина называется дискретной, если она принимает не более, чем счетное множество значений. Отметим, что само пространство при этом может быть и несчетным. Простейшей формой закона распределения дискретной случайной величины (далее, ДСВ) является ряд распределения – таблица, в верхней строке которой перечислены все возможные значения случайной величины А в нижней строке – соответствующие им вероятности

			. . .		. . .
p			. . .		. . .

«График» ряда распределения, получающийся путем соединения точек с координатами отрезками прямых линий, называется многоугольником распределения (см. рис. ниже).

p

•

• •

• •

. . .

Многоугольник распределения.

График функции распределения ДСВ является ступенчатым, и у него скачки возникают в точках возможных значений СВ, и равны они соответствующим вероятностям

p=1

. . .

. . .